27.2.1 第3课时 两边成比例且夹角相等的两个三角形相似 同步导学案(含答案)
文档属性
| 名称 | 27.2.1 第3课时 两边成比例且夹角相等的两个三角形相似 同步导学案(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 20:52:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.2.1 相似三角形的判定
第3课时 两边成比例且夹角相等的两个三角形相似
学习目标:1. 探索“两边成比例且夹角相等的两个三角形相似”的判定定理.
2. 会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
一、知识链接
1. 回忆我们学习过的判定三角形相似的方法. 类比证明三角形全等的方法,猜想证明三角形相似还有哪些方法?21世纪教育网版权所有
2. 类似于判定三角形全等的 SAS 方法,能不能通过两边和夹角来判定两个三角形相似呢?
1、要点探究
探究点1:两边成比例且夹角相等的两个三角形相似
操作 利用刻度尺和量角器画 △ABC和 △A′B′C′,使∠A=∠A′,,量出 BC 及 B′C′ 的长,它们的比值等于 k 吗?再量一量两个三角形另外的两个角,你有什么发现?△ABC 与 △A′B′C′ 有何关系?21cnjy.com
思考 改变 k 和∠A 的值的大小,是否有同样的结论?
证明 如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,,求证:△ABC∽△A′B′C′.【来源:21·世纪·教育·网】
证明:在 △A′B′C′ 的边 A′B′ ( http: / / www.21cnjy.com )上截取点D,使 A′D = AB.过点 D 作 DE∥ B′C′,交 A′C′ 于点 E.【补全后面的证明过程】21·世纪*教育网
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【要点归纳】由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:∵,∠A=∠A′,∴ △ABC ∽ △A′B′C′ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
思考 对于△ABC和 △A′B′C′,如果∠B= ∠B′,,这两个三角形一定会相似吗?试着画画看.21教育网
【结论】如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.2·1·c·n·j·y
【典例精析】
例1 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm ,A′C′=6 cm.www-2-1-cnjy-com
【针对训练】在 △ABC 和 △DEF ( http: / / www.21cnjy.com ) 中,∠C =∠F=70°,AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF =1.5 cm. 求证:△DEF∽△ABC.2-1-c-n-j-y
例2 如图,△ABC 与 △ADE 都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE. 求证:△ABC ∽△ADE.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
例3 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且,求 DE 的长.【出处:21教育名师】
( http: / / www.21cnjy.com )
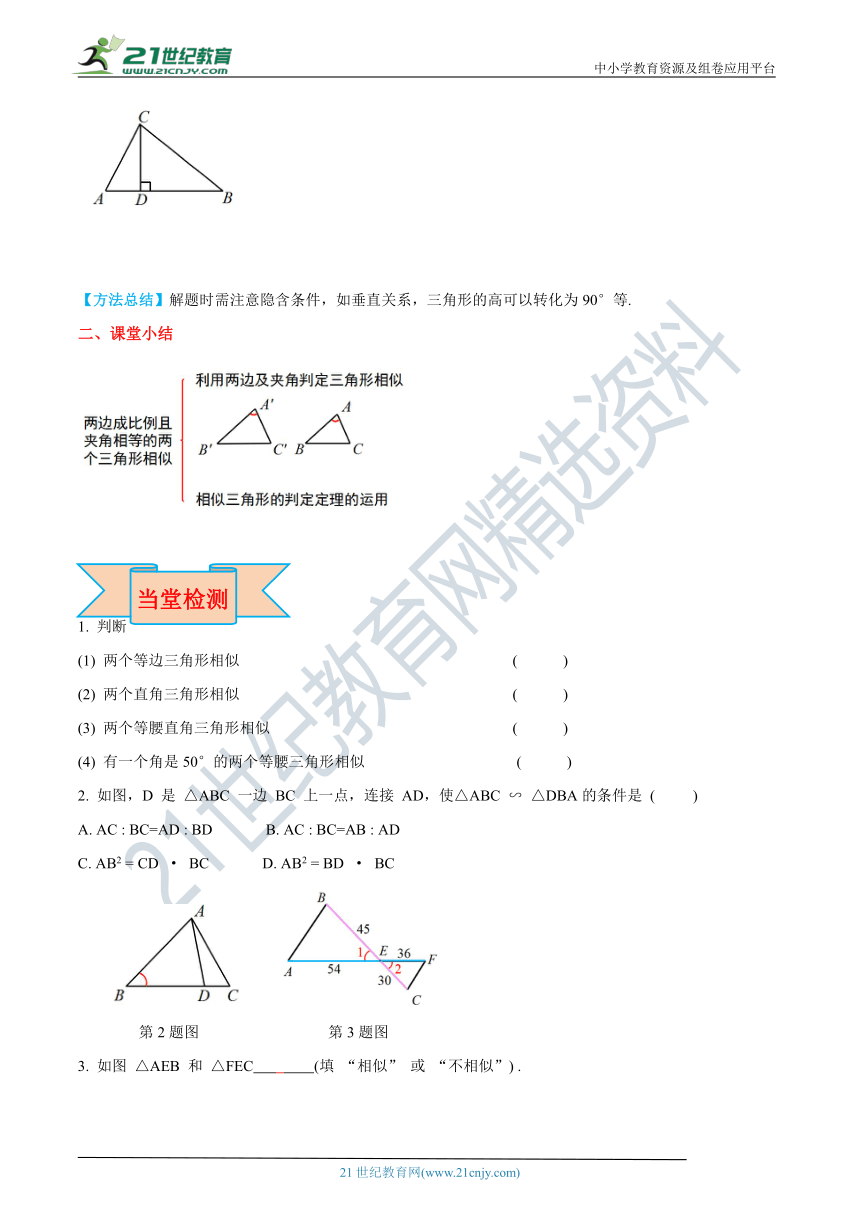
例4 如图,在 △ABC 中,CD 是边 AB 上的高,且,求证: ∠ACB=90°.
( http: / / www.21cnjy.com )
【方法总结】解题时需注意隐含条件,如垂直关系,三角形的高可以转化为90°等.
二、课堂小结
( http: / / www.21cnjy.com )
1. 判断
(1) 两个等边三角形相似 ( )21*cnjy*com
(2) 两个直角三角形相似 ( )【版权所有:21教育】
(3) 两个等腰直角三角形相似 ( )21教育名师原创作品
(4) 有一个角是50°的两个等腰三角形相似 ( )
2. 如图,D 是 △ABC 一边 BC 上一点,连接 AD,使△ABC ∽ △DBA的条件是 ( )
A. AC : BC=AD : BD B. AC : BC=AB : AD
C. AB2 = CD · BC D. AB2 = BD · BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第2题图 第3题图
3. 如图 △AEB 和 △FEC (填 “相似” 或 “不相似”) .
4. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5,CD=,求 AD 的长.
( http: / / www.21cnjy.com )
5. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,求证 △ABC ∽△AED. 21·cn·jy·com
( http: / / www.21cnjy.com )
拓展提升
6. 如图,已知 △AB ( http: / / www.21cnjy.com )C中,D 为边 AC 上一点,P 为边AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长度为 时,△ADP 和 △ABC 相似.21*cnjy*com
( http: / / www.21cnjy.com )
参考答案
自主学习
一、知识链接
1. 解:三角形全等的判定方法有SSS、SAS、ASA、AAS、HL;相似也可以有SAS和HL.
2. 解:能.
合作探究
一、要点探究
探究点1:两边成比例且夹角相等的两个三角形相似
证明 解:∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.∴.
∵ A′D=AB,,∴,∴ A′E = AC .
又 ∠A′ = ∠A.∴ △A′DE ≌ △ABC, ∴ △A′B′C′ ∽ △ABC.
【典例精析】
例1 解:∵ ,,∴,
又 ∠A′ = ∠A,∴ △ABC ∽ △A′B′C′.
【针对训练】证明:∵ AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF = 1.5 cm,∴.又 ∵∠C =∠F = 70°,∴ △DEF ∽△ABC.www.21-cn-jy.com
例2 证明:∵ △ABC 与 △ADE都 是等腰三角形,∴ AD =AE,AB = AC,∴,又 ∵∠DAB = ∠CAE,∴ ∠DAB +∠BAE = ∠CAE +∠BAE,
即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
例3 解:∵ AE=1.5,AC=2, ∴.又∵∠EAD=∠CAB,∴ △ADE ∽△ABC,∴,∴.
例4 证明: ∵ CD 是边 AB 上的高,∴ ∠ADC =∠CDB =90°.
∵,∴△ADC ∽△CDB.∴ ∠ACD =∠B.
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
当堂检测
1. (1) √ (2) × (3) × (4) × 2. D 3. 相似
4. 解:∵AB=6,BC=4,AC=5,CD=,∴.
又∵∠B=∠ACD,∴ △ABC ∽ △DCA,∴,∴AD=.
5. 证明:∵ AB · AD = AE·AC,∴.
又∵ ∠DAB =∠CAE,∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,∴ △ABC ∽△AED.
拓展提升
6. 4 或 9
解析:当 △ADP ∽△ ( http: / / www.21cnjy.com )ACB 时,AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,解得 AP = 9;当 △ADP ∽△ABC 时,AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,解得 AP = 4.∴ 当 AP 的长度为 4 或 9 时,△ADP 和 △ABC 相似.
( http: / / www.21cnjy.com )
自主学习
合作探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.2.1 相似三角形的判定
第3课时 两边成比例且夹角相等的两个三角形相似
学习目标:1. 探索“两边成比例且夹角相等的两个三角形相似”的判定定理.
2. 会根据边和角的关系来判定两个三角形相似,并进行相关计算. (重点、难点)
一、知识链接
1. 回忆我们学习过的判定三角形相似的方法. 类比证明三角形全等的方法,猜想证明三角形相似还有哪些方法?21世纪教育网版权所有
2. 类似于判定三角形全等的 SAS 方法,能不能通过两边和夹角来判定两个三角形相似呢?
1、要点探究
探究点1:两边成比例且夹角相等的两个三角形相似
操作 利用刻度尺和量角器画 △ABC和 △A′B′C′,使∠A=∠A′,,量出 BC 及 B′C′ 的长,它们的比值等于 k 吗?再量一量两个三角形另外的两个角,你有什么发现?△ABC 与 △A′B′C′ 有何关系?21cnjy.com
思考 改变 k 和∠A 的值的大小,是否有同样的结论?
证明 如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,,求证:△ABC∽△A′B′C′.【来源:21·世纪·教育·网】
证明:在 △A′B′C′ 的边 A′B′ ( http: / / www.21cnjy.com )上截取点D,使 A′D = AB.过点 D 作 DE∥ B′C′,交 A′C′ 于点 E.【补全后面的证明过程】21·世纪*教育网
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
【要点归纳】由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:∵,∠A=∠A′,∴ △ABC ∽ △A′B′C′ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
思考 对于△ABC和 △A′B′C′,如果∠B= ∠B′,,这两个三角形一定会相似吗?试着画画看.21教育网
【结论】如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.2·1·c·n·j·y
【典例精析】
例1 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm ,A′C′=6 cm.www-2-1-cnjy-com
【针对训练】在 △ABC 和 △DEF ( http: / / www.21cnjy.com ) 中,∠C =∠F=70°,AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF =1.5 cm. 求证:△DEF∽△ABC.2-1-c-n-j-y
例2 如图,△ABC 与 △ADE 都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE. 求证:△ABC ∽△ADE.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
例3 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且,求 DE 的长.【出处:21教育名师】
( http: / / www.21cnjy.com )
例4 如图,在 △ABC 中,CD 是边 AB 上的高,且,求证: ∠ACB=90°.
( http: / / www.21cnjy.com )
【方法总结】解题时需注意隐含条件,如垂直关系,三角形的高可以转化为90°等.
二、课堂小结
( http: / / www.21cnjy.com )
1. 判断
(1) 两个等边三角形相似 ( )21*cnjy*com
(2) 两个直角三角形相似 ( )【版权所有:21教育】
(3) 两个等腰直角三角形相似 ( )21教育名师原创作品
(4) 有一个角是50°的两个等腰三角形相似 ( )
2. 如图,D 是 △ABC 一边 BC 上一点,连接 AD,使△ABC ∽ △DBA的条件是 ( )
A. AC : BC=AD : BD B. AC : BC=AB : AD
C. AB2 = CD · BC D. AB2 = BD · BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第2题图 第3题图
3. 如图 △AEB 和 △FEC (填 “相似” 或 “不相似”) .
4. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5,CD=,求 AD 的长.
( http: / / www.21cnjy.com )
5. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,求证 △ABC ∽△AED. 21·cn·jy·com
( http: / / www.21cnjy.com )
拓展提升
6. 如图,已知 △AB ( http: / / www.21cnjy.com )C中,D 为边 AC 上一点,P 为边AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长度为 时,△ADP 和 △ABC 相似.21*cnjy*com
( http: / / www.21cnjy.com )
参考答案
自主学习
一、知识链接
1. 解:三角形全等的判定方法有SSS、SAS、ASA、AAS、HL;相似也可以有SAS和HL.
2. 解:能.
合作探究
一、要点探究
探究点1:两边成比例且夹角相等的两个三角形相似
证明 解:∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.∴.
∵ A′D=AB,,∴,∴ A′E = AC .
又 ∠A′ = ∠A.∴ △A′DE ≌ △ABC, ∴ △A′B′C′ ∽ △ABC.
【典例精析】
例1 解:∵ ,,∴,
又 ∠A′ = ∠A,∴ △ABC ∽ △A′B′C′.
【针对训练】证明:∵ AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF = 1.5 cm,∴.又 ∵∠C =∠F = 70°,∴ △DEF ∽△ABC.www.21-cn-jy.com
例2 证明:∵ △ABC 与 △ADE都 是等腰三角形,∴ AD =AE,AB = AC,∴,又 ∵∠DAB = ∠CAE,∴ ∠DAB +∠BAE = ∠CAE +∠BAE,
即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
例3 解:∵ AE=1.5,AC=2, ∴.又∵∠EAD=∠CAB,∴ △ADE ∽△ABC,∴,∴.
例4 证明: ∵ CD 是边 AB 上的高,∴ ∠ADC =∠CDB =90°.
∵,∴△ADC ∽△CDB.∴ ∠ACD =∠B.
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
当堂检测
1. (1) √ (2) × (3) × (4) × 2. D 3. 相似
4. 解:∵AB=6,BC=4,AC=5,CD=,∴.
又∵∠B=∠ACD,∴ △ABC ∽ △DCA,∴,∴AD=.
5. 证明:∵ AB · AD = AE·AC,∴.
又∵ ∠DAB =∠CAE,∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,∴ △ABC ∽△AED.
拓展提升
6. 4 或 9
解析:当 △ADP ∽△ ( http: / / www.21cnjy.com )ACB 时,AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,解得 AP = 9;当 △ADP ∽△ABC 时,AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,解得 AP = 4.∴ 当 AP 的长度为 4 或 9 时,△ADP 和 △ABC 相似.
( http: / / www.21cnjy.com )
自主学习
合作探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
