28.2.2 第2课时 利用仰俯角解直角三角形 同步导学案(含答案)
文档属性
| 名称 | 28.2.2 第2课时 利用仰俯角解直角三角形 同步导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
第2课时 利用仰俯角解直角三角形
学习目标:
1.巩固解直角三角形有关知识.
2.能运用解直角三角形知识 ( http: / / www.21cnjy.com )解决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 21教育网
重点:1.巩固解直角三角形相关知识.
2.能运用解直角三角形知识解 ( http: / / www.21cnjy.com )决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 21·世纪*教育网
难点:能运用解直角三角形知识解决仰角和俯角有 ( http: / / www.21cnjy.com )关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 【版权所有:21教育】
1、知识链接
1.什么叫仰角?什么叫俯角?
2. 填空:(1)sin 30°= ,cos 60°= ,tan 45°= ;21*cnjy*com
(2)sin 45°cos 45°= ,cos 30°cos 60°= ;
(2)sin2 15°+cos215°= ,tan 30°tan 60°= .
1、要点探究
探究点1:解与仰俯角有关的问题
【典例精析】
例1 热气球的探测器显 ( http: / / www.21cnjy.com )示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).www.21-cn-jy.com
( http: / / www.21cnjy.com )
分析:我们知道,在视线与水平线所成 ( http: / / www.21cnjy.com )的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.在Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
练一练 建筑物BC上有一旗杆AB,由距BC ( http: / / www.21cnjy.com )40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).21教育名师原创作品
( http: / / www.21cnjy.com )
【典例精析】
例2 如图,小明想测量塔AB的高度. ( http: / / www.21cnjy.com )他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处,测得仰角为60°,小明的身高为1.5 m.那么该塔有多高 (结果精确到1 m),你能帮小明算出该塔有多高吗 2-1-c-n-j-y
( http: / / www.21cnjy.com )
分析:由图可知,塔高AB可以分为两部分,上部分AB′可以在Rt△AD′B′和Rt△AC′B′中利用仰角的正切值求出,B′B与D′D相等.
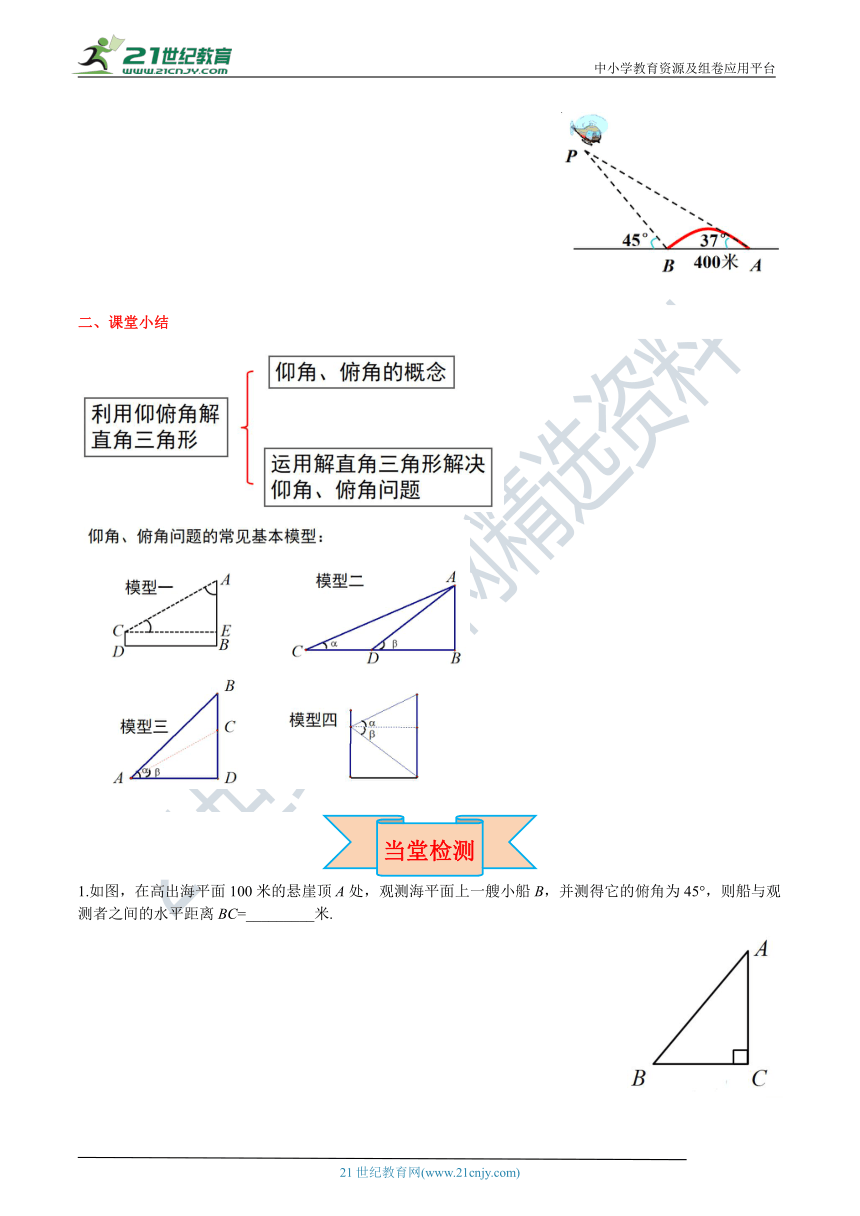
练一练 如图,直升飞机在长400米 ( http: / / www.21cnjy.com )的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度.(结果取整数. 参考数据:sin37°≈0.8,2·1·c·n·j·y
cos37 °≈0.6,tan 37°≈0.75)
( http: / / www.21cnjy.com )
二、课堂小结
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
1.如图,在高出海平面100米的悬崖顶A处, ( http: / / www.21cnjy.com )观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.www-2-1-cnjy-com
( http: / / www.21cnjy.com )
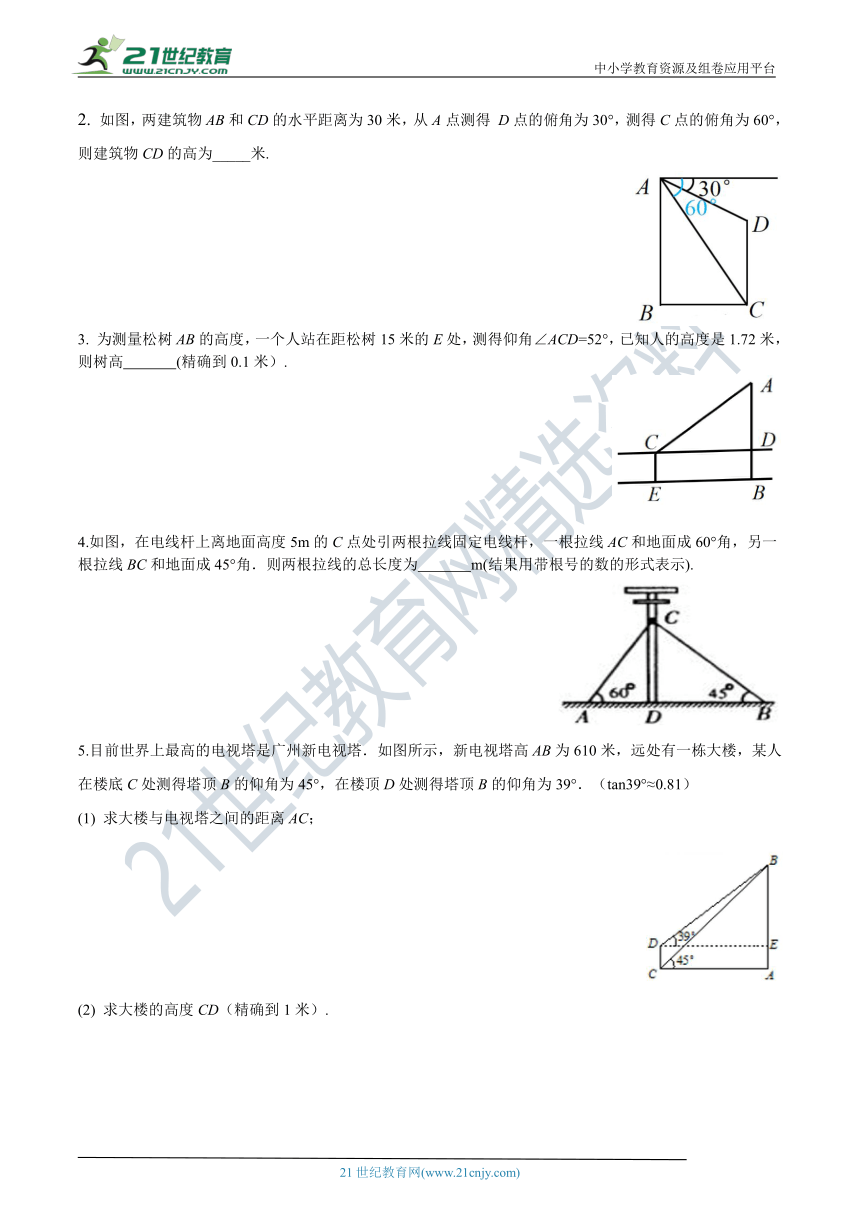
2. 如图,两建筑物AB和CD的水平距离为30米,从A点测得 D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.【出处:21教育名师】
( http: / / www.21cnjy.com )
3. 为测量松树AB的高度, ( http: / / www.21cnjy.com )一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度是1.72米,则树高 (精确到0.1米).
( http: / / www.21cnjy.com )
4.如图,在电线杆上离地面高度5m ( http: / / www.21cnjy.com )的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示).
( http: / / www.21cnjy.com )
5.目前世界上最高的电视 ( http: / / www.21cnjy.com )塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
( http: / / www.21cnjy.com )
(2) 求大楼的高度CD(精确到1米).
6. 如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .
( http: / / www.21cnjy.com )
参考答案
自主学习
一、知识链接
1.在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.21世纪教育网版权所有
2.(1) 1 (2) (3) 1 121cnjy.com
课堂探究
一、要点探究
探究点1:解与仰俯角有关的问题
【典例精析】
例1 解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
练一练 解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m. 在Rt△ACD中,
tan ∠ADC=,∴AC=tan∠ADC·DC=tan 54°×40≈55.1(m),
∴AB=AC - BC=55.1-40=15.1(m). 21·cn·jy·com
【典例精析】
例2 解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°, D′C′=50m.∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设AB′=x m.【来源:21·世纪·教育·网】
练一练 解:作PO⊥AB交AB的延长线于点O.设PO=x米,在Rt△POB中,∠PBO=45°,OB=PO= x米.在Rt△POA中,∠PAB=37°,即解得x=1200.故飞机的高度为1200米.21*cnjy*com
当堂检测
1. 100 2. 3. 20.9 米 4.
5. 解:(1)由题意,AC=AB=610(米).(2)DE=AC=610(米),在Rt△BDE中,
tan∠BDE=.故BE=DEtan39°. ∵CD=AE,∴CD=AB-BE=AB-DE·tan39°=610-610×tan39°≈116(米).【来源:21cnj*y.co*m】
6.解:如图,过点P作PC⊥BA的延长线于点C.则∠PBO=∠CPB=45°,∠CPA=30°,∴PC=BC=200+AC,tan30°=∴AC=()米,PO=BC=米. .
( http: / / www.21cnjy.com )
自主学习
合作探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
第2课时 利用仰俯角解直角三角形
学习目标:
1.巩固解直角三角形有关知识.
2.能运用解直角三角形知识 ( http: / / www.21cnjy.com )解决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 21教育网
重点:1.巩固解直角三角形相关知识.
2.能运用解直角三角形知识解 ( http: / / www.21cnjy.com )决仰角和俯角有关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 21·世纪*教育网
难点:能运用解直角三角形知识解决仰角和俯角有 ( http: / / www.21cnjy.com )关的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. 【版权所有:21教育】
1、知识链接
1.什么叫仰角?什么叫俯角?
2. 填空:(1)sin 30°= ,cos 60°= ,tan 45°= ;21*cnjy*com
(2)sin 45°cos 45°= ,cos 30°cos 60°= ;
(2)sin2 15°+cos215°= ,tan 30°tan 60°= .
1、要点探究
探究点1:解与仰俯角有关的问题
【典例精析】
例1 热气球的探测器显 ( http: / / www.21cnjy.com )示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).www.21-cn-jy.com
( http: / / www.21cnjy.com )
分析:我们知道,在视线与水平线所成 ( http: / / www.21cnjy.com )的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.在Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
练一练 建筑物BC上有一旗杆AB,由距BC ( http: / / www.21cnjy.com )40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).21教育名师原创作品
( http: / / www.21cnjy.com )
【典例精析】
例2 如图,小明想测量塔AB的高度. ( http: / / www.21cnjy.com )他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处,测得仰角为60°,小明的身高为1.5 m.那么该塔有多高 (结果精确到1 m),你能帮小明算出该塔有多高吗 2-1-c-n-j-y
( http: / / www.21cnjy.com )
分析:由图可知,塔高AB可以分为两部分,上部分AB′可以在Rt△AD′B′和Rt△AC′B′中利用仰角的正切值求出,B′B与D′D相等.
练一练 如图,直升飞机在长400米 ( http: / / www.21cnjy.com )的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度.(结果取整数. 参考数据:sin37°≈0.8,2·1·c·n·j·y
cos37 °≈0.6,tan 37°≈0.75)
( http: / / www.21cnjy.com )
二、课堂小结
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
1.如图,在高出海平面100米的悬崖顶A处, ( http: / / www.21cnjy.com )观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.www-2-1-cnjy-com
( http: / / www.21cnjy.com )
2. 如图,两建筑物AB和CD的水平距离为30米,从A点测得 D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.【出处:21教育名师】
( http: / / www.21cnjy.com )
3. 为测量松树AB的高度, ( http: / / www.21cnjy.com )一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度是1.72米,则树高 (精确到0.1米).
( http: / / www.21cnjy.com )
4.如图,在电线杆上离地面高度5m ( http: / / www.21cnjy.com )的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示).
( http: / / www.21cnjy.com )
5.目前世界上最高的电视 ( http: / / www.21cnjy.com )塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
( http: / / www.21cnjy.com )
(2) 求大楼的高度CD(精确到1米).
6. 如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .
( http: / / www.21cnjy.com )
参考答案
自主学习
一、知识链接
1.在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.21世纪教育网版权所有
2.(1) 1 (2) (3) 1 121cnjy.com
课堂探究
一、要点探究
探究点1:解与仰俯角有关的问题
【典例精析】
例1 解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
练一练 解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m. 在Rt△ACD中,
tan ∠ADC=,∴AC=tan∠ADC·DC=tan 54°×40≈55.1(m),
∴AB=AC - BC=55.1-40=15.1(m). 21·cn·jy·com
【典例精析】
例2 解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°, D′C′=50m.∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设AB′=x m.【来源:21·世纪·教育·网】
练一练 解:作PO⊥AB交AB的延长线于点O.设PO=x米,在Rt△POB中,∠PBO=45°,OB=PO= x米.在Rt△POA中,∠PAB=37°,即解得x=1200.故飞机的高度为1200米.21*cnjy*com
当堂检测
1. 100 2. 3. 20.9 米 4.
5. 解:(1)由题意,AC=AB=610(米).(2)DE=AC=610(米),在Rt△BDE中,
tan∠BDE=.故BE=DEtan39°. ∵CD=AE,∴CD=AB-BE=AB-DE·tan39°=610-610×tan39°≈116(米).【来源:21cnj*y.co*m】
6.解:如图,过点P作PC⊥BA的延长线于点C.则∠PBO=∠CPB=45°,∠CPA=30°,∴PC=BC=200+AC,tan30°=∴AC=()米,PO=BC=米. .
( http: / / www.21cnjy.com )
自主学习
合作探究
当堂检测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
