华东师大版数学九年级上册 23.4 中位线 课件 (共24张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.4 中位线 课件 (共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 12:30:21 | ||
图片预览




文档简介
(共23张PPT)
23.4 中位线
教学目标
1.知识目标:通过画图,亲身体验三角形中位线的概念以及与三角形中线的区别,掌握三角形中位线定理。
2.能力目标:通过三角形中位线定理的证明,渗透数学学习中的转化思想。
3.情感目标:培养学生自主探究、猜想、推理论证的能力,并能应用所学的知识解决问题,通过变式练习,小组讨论、交流等活动,培养良好的学习态度以及自主意识和合作精神。
教学重点、难点
1.教学重点:三角形的中位线定理以及定理的证明过程,应用三角形中位线定理解决问题。
2.教学难点:运用三角形中位线定理如何添加辅助线是本节的教学难点。
A
B
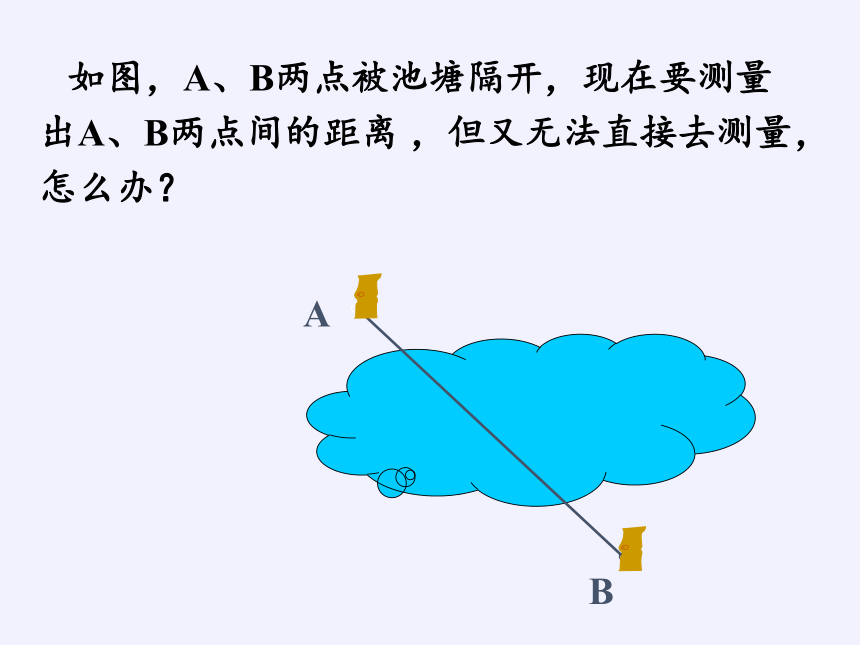
问题:A、B两点被池塘隔开,如何测量A、B两点距离,但又无法直接去测量,怎么办?
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?
A
B
。
。
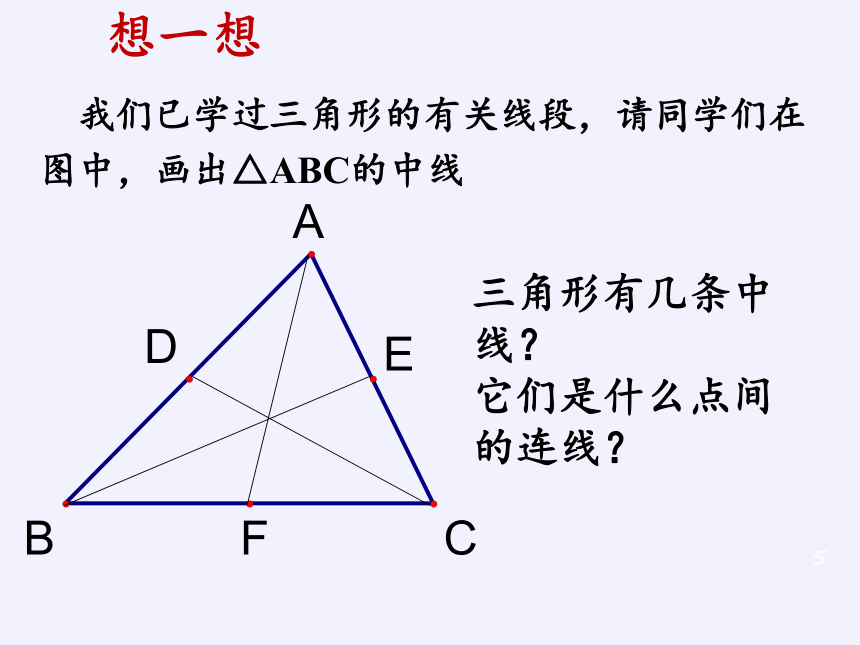
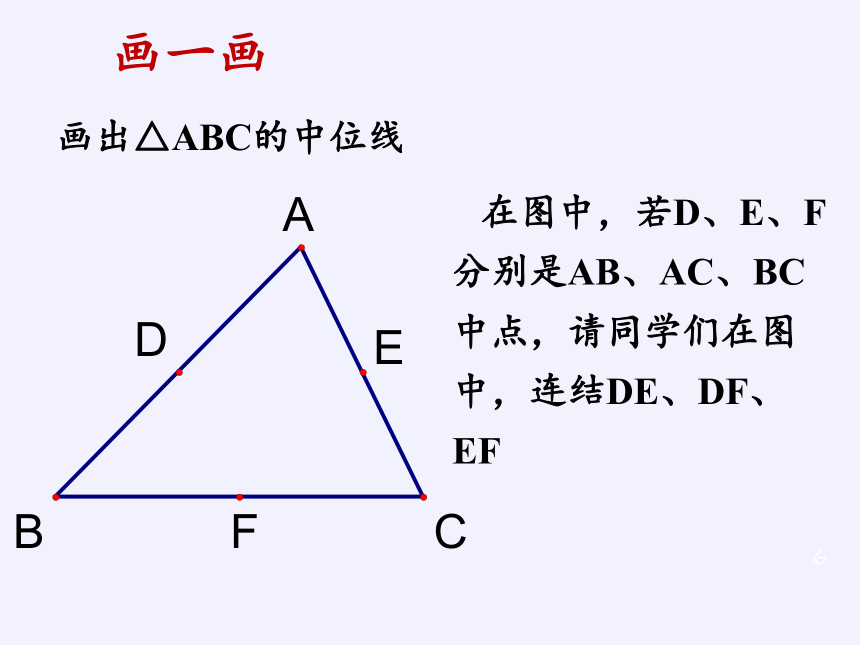
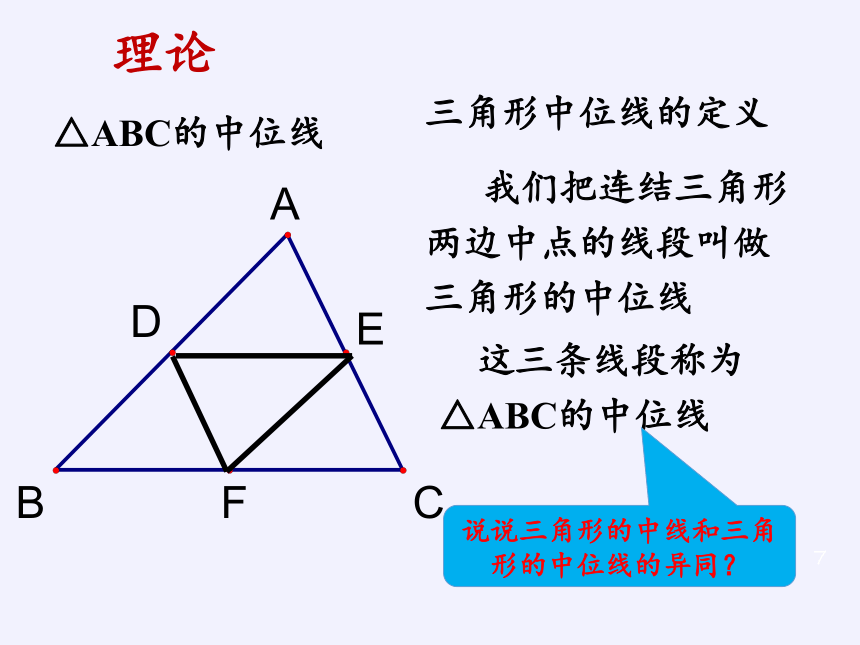
我们已学过三角形的有关线段,请同学们在图中,画出△ABC的中线三角形有几条中线?它们是什么点间的连线?想一想画出△ABC的中位线在图中,若D、E、F分别是AB、AC、BC中点,请同学们在图中,连结DE、DF、EF画一画△ABC的中位线这三条线段称为△ABC的中位线三角形中位线的定义我们把连结三角形两边中点的线段叫做三角形的中位线说说三角形的中线和三角形的中位线的异同?理论
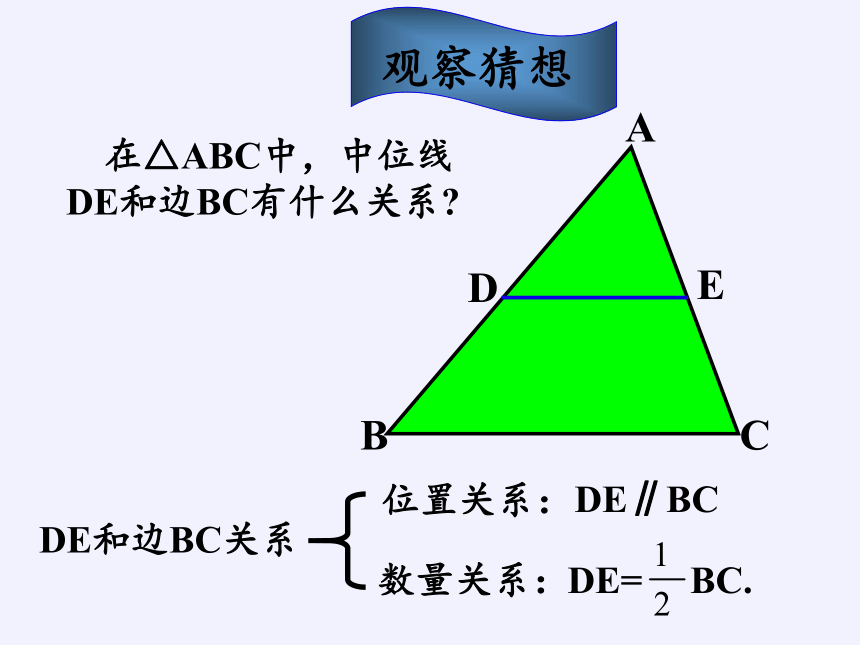
观察猜想
在△ABC中,中位线DE和边BC有什么关系
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE= BC.
A
B
C
D
E
已知:如图,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,命题:三角形的中位线平行于第三边,并且等于第三边的一半.你能证明这个命题吗 理论已知:如图,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,证一证三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.理论已知:如果,点D、E、F分别是△ABC的三边的中点.
(1)若AB=8cm,求EF的长;
(2)若DE=5cm,求BC的长.
(3)若增加M、N分别是BD、BF的中点,
问MN与AC有什么关系?为什么?
演练
4cm
10cm
MN//AC;MN= AC
例1、求证三角形的一条中位线与第三边上的中线互相平分.ABCDE已知:如图,在△ABC中,AD=DB,AE=EC,BF=FC求证:DE、AF互相平分F证明:连结DF、EF∵AD=DB,BE=CE∴DE∥AC(三角形中位线定理)同理EF∥AB∴四边形ADEF是平行四边形∴DE、AF互相平分(平行四边形的对角线互相平分)运用运用例2如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: 拓展三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的如图,A、B两棵树被池塘隔开,现在要测量出A、B两树间的距离 ,但又无法直接去测量,怎么办?DE是中位线回归课堂检测
1.用其它的方法来证明三角形中位线的性质.
2.如何将三角形蛋糕切成相等的四块
3.求证:顺次连结四边形各边的中点所
得的四边形是平行四边形。
如图:在△ABC中,D是AC的中点,E是AB的中点。
则有:
DE∥BC,
DE= BC.
2
1
D
A
B
C
E
F
分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CDF,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
第一题
按照图上蛋糕可以切成相等的四块第二题已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形.第三题本课小结
1.理解三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3.三角形重心的定义和性质:三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的
1、第79页练习 第1题
2、第79页习题23.4 第1、2题
布置作业
谢 谢
23.4 中位线
教学目标
1.知识目标:通过画图,亲身体验三角形中位线的概念以及与三角形中线的区别,掌握三角形中位线定理。
2.能力目标:通过三角形中位线定理的证明,渗透数学学习中的转化思想。
3.情感目标:培养学生自主探究、猜想、推理论证的能力,并能应用所学的知识解决问题,通过变式练习,小组讨论、交流等活动,培养良好的学习态度以及自主意识和合作精神。
教学重点、难点
1.教学重点:三角形的中位线定理以及定理的证明过程,应用三角形中位线定理解决问题。
2.教学难点:运用三角形中位线定理如何添加辅助线是本节的教学难点。
A
B
问题:A、B两点被池塘隔开,如何测量A、B两点距离,但又无法直接去测量,怎么办?
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?
A
B
。
。
我们已学过三角形的有关线段,请同学们在图中,画出△ABC的中线三角形有几条中线?它们是什么点间的连线?想一想画出△ABC的中位线在图中,若D、E、F分别是AB、AC、BC中点,请同学们在图中,连结DE、DF、EF画一画△ABC的中位线这三条线段称为△ABC的中位线三角形中位线的定义我们把连结三角形两边中点的线段叫做三角形的中位线说说三角形的中线和三角形的中位线的异同?理论
观察猜想
在△ABC中,中位线DE和边BC有什么关系
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE= BC.
A
B
C
D
E
已知:如图,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,命题:三角形的中位线平行于第三边,并且等于第三边的一半.你能证明这个命题吗 理论已知:如图,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,证一证三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.理论已知:如果,点D、E、F分别是△ABC的三边的中点.
(1)若AB=8cm,求EF的长;
(2)若DE=5cm,求BC的长.
(3)若增加M、N分别是BD、BF的中点,
问MN与AC有什么关系?为什么?
演练
4cm
10cm
MN//AC;MN= AC
例1、求证三角形的一条中位线与第三边上的中线互相平分.ABCDE已知:如图,在△ABC中,AD=DB,AE=EC,BF=FC求证:DE、AF互相平分F证明:连结DF、EF∵AD=DB,BE=CE∴DE∥AC(三角形中位线定理)同理EF∥AB∴四边形ADEF是平行四边形∴DE、AF互相平分(平行四边形的对角线互相平分)运用运用例2如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: 拓展三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的如图,A、B两棵树被池塘隔开,现在要测量出A、B两树间的距离 ,但又无法直接去测量,怎么办?DE是中位线回归课堂检测
1.用其它的方法来证明三角形中位线的性质.
2.如何将三角形蛋糕切成相等的四块
3.求证:顺次连结四边形各边的中点所
得的四边形是平行四边形。
如图:在△ABC中,D是AC的中点,E是AB的中点。
则有:
DE∥BC,
DE= BC.
2
1
D
A
B
C
E
F
分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CDF,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
第一题
按照图上蛋糕可以切成相等的四块第二题已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形.第三题本课小结
1.理解三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3.三角形重心的定义和性质:三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的
1、第79页练习 第1题
2、第79页习题23.4 第1、2题
布置作业
谢 谢
