2.3三角形内角和教案 四年级数学下册北师大版
文档属性
| 名称 | 2.3三角形内角和教案 四年级数学下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 984.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 18:10:01 | ||
图片预览


文档简介
2.3 三角形的内角和
一、教学目标:
1.知识与技能:
通过测量、撕拼、折叠等方法,探索和发现三角形三个内角的和等于180°。知道三角形两个角的度数,能求出第三个角的度数。能应用三角形内角和的性质解决一些简单的问题。
2.过程与方法:发展学生动手操作、观察比较和抽象概括的能力。
3.情感、态度与价值观:体验数学活动的探索乐趣,体会研究数学问题的思想方法。
二、课时安排:1课时
三、教学重点:
让学生经历“三角形内角和是180°”这一知识的形成、发展和应用的全过程。
四、教学难点:
能应用三角形的内角和的性质解决一些简单问题。
五、教学过程
(一)导入新课
设疑激趣,现在三角形家族为了一件事正在争论,我们来帮帮它们。(播放课件)
同学们,现在出现了两种不同的意见,有的认为大三角形的内角和大,还有的认为两个三角形的内角和的度数都是一样的。那么到底谁说得对呢
这节课我们就一起来研究这个问题。(板书课题:三角形的内角和)
(二)讲授新课
动手操作,探究新知
1、探究特殊三角形的内角和
师拿出两个三角板,问:它们是什么三角形?
请大家拿出自己的两个三角尺,在小组内说说每一个三角尺上三个角的度数,并求出这两个直角三角形的内角和。
从刚才两个三角形内角和的计算中,你们发现了什么?
2、探究一般三角形内角和
(1)猜一猜。
猜一猜:那么,其它三角形的内角和是多少度呢?(可能是180°)
(2)操作、验证一般三角形内角和是180°。
所有三角形的内角和究竟是不是180°,你能用什么办法来证明,使别人相信呢?
那就请大家在小组共同计算吧!
请每个同学都拿出自己准备的不同的三角形,并量出每个内角的度数,求出它们的内角和,把结果填在表中:
(三)重难点精讲
1.小组汇报结果。
提问:你们发现了什么?
得出三角形的内角和有等于180°的,也有接近180°的。
提出质疑:测量中为什么会出现不同的结果呢?
指名学生说一说:测量有误差。
小结:通过测量计算我们发现每个三角形的三个内角和都在180°左右。
2.继续探究
(1)动手操作,验证猜测。
大家的意见不统一,结论不一样,怎么办?还有其它办法吗?请同学们动脑筋想一想能通过动手操作来验证吗?
(先小组讨论,再汇报方法)
大家的办法都很好,请你们小组合作,动手操作。
(2)学生操作,教师巡视指导。
(3)全班交流汇报验证方法、结果。
学生放在投影仪上展示给大家看。(剪拼、撕拼、折拼)
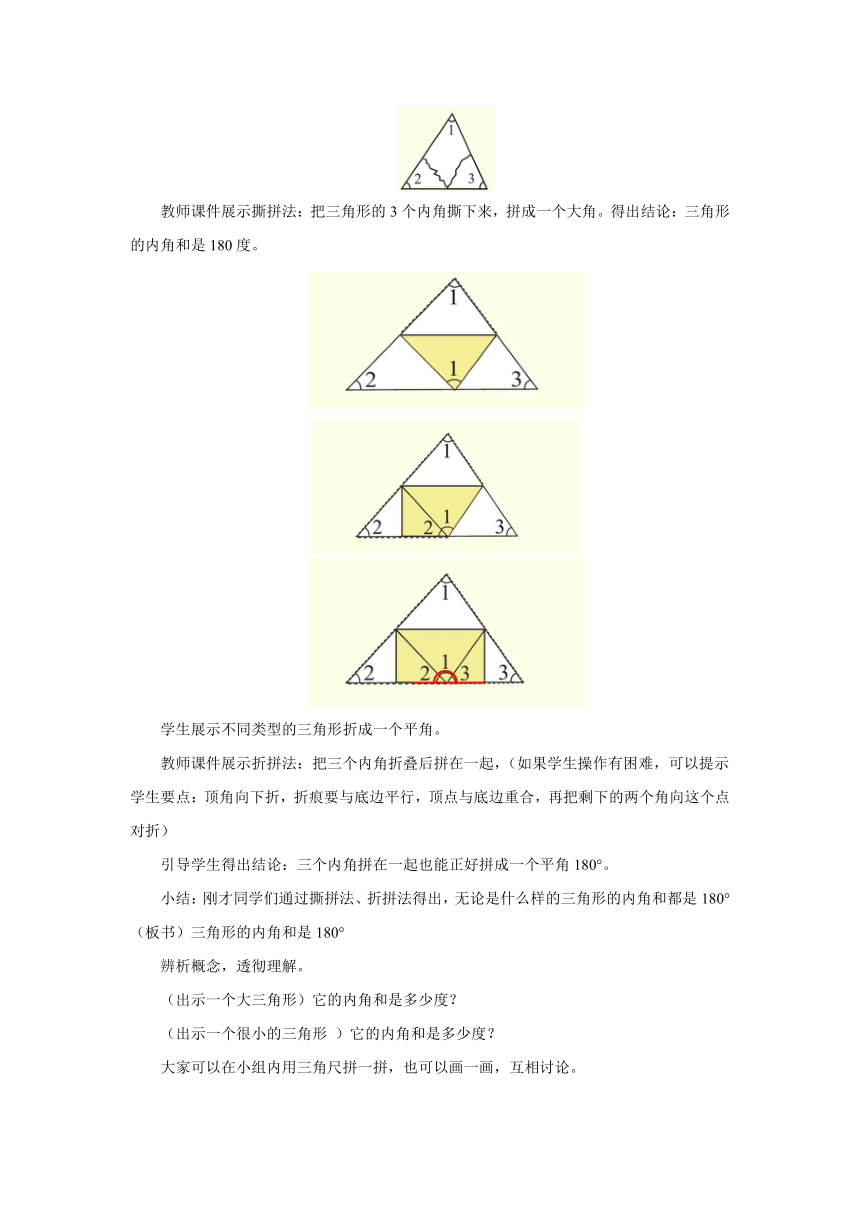
教师课件展示撕拼法:把三角形的3个内角撕下来,拼成一个大角。得出结论:三角形的内角和是180度。
学生展示不同类型的三角形折成一个平角。
教师课件展示折拼法:把三个内角折叠后拼在一起,(如果学生操作有困难,可以提示学生要点:顶角向下折,折痕要与底边平行,顶点与底边重合,再把剩下的两个角向这个点对折)
引导学生得出结论:三个内角拼在一起也能正好拼成一个平角180°。
小结:刚才同学们通过撕拼法、折拼法得出,无论是什么样的三角形的内角和都是180°(板书)三角形的内角和是180°
辨析概念,透彻理解。
(出示一个大三角形)它的内角和是多少度?
(出示一个很小的三角形 )它的内角和是多少度?
大家可以在小组内用三角尺拼一拼,也可以画一画,互相讨论。
经过一翻激烈的讨论探究后,学生发现: 三角形不论位置、大小、形状如何,它的内角和总是180°
归纳小结
刚才同学们用很多方法证明了什么?现在齐读板书: “三角形的内角和是180°”。
(五)随堂检测
1.猜一猜,可能是什么三角形?
引导学生理解,利用三角形内角和是180度和三角形的分类来解答。
你还能猜出是什么三角形吗?
学生可能会想到,等边三角形每个角都是60度,遮住的是等边三角形。
也可以通过计算解答。
2.引导学生理解,知道每个三角尺的每个角的度数,通过计算得出,每个内角的度数。
了解,四边形的内角和是360度。
3. 让学生动手操作,小组合作。
4. 猜一猜,可能是什么三角形?
第1个,只能是钝角三角形。
第2个,锐角三角形、直角三角形和钝角三角形都有可能。
第3个,只能是锐角三角形。
5.独立完成
小结: 三角形内角和是180 ° 。
六、板书设计
三角形内角和
剪 拼 折
锐角三角形 35°+66°+79°=180°
直角三角形 90°+37°+53°=180°
钝角三角形 112°+35°+32°=179°
三角形的内角和是180°
七、作业布置
完成练一练第7题。
八、教学反思
三角形的内角和是三角形的一个重要特征。本课是安排在学习三角形的概念及分类之后进行的,它是学生以后学习多边形的内角和及解决其它实际问题的基础。学生在掌握知识方面:已经掌握了三角形的分类,比较熟悉平角等有关知识;能力方面:经过三年多的学习,已具备了初步的动手操作能力和主动探究能力以及合作学习的习惯。因此,教材很重视知识的探索与发现,安排了一系列的实验操作活动。教材呈现教学内容时,不但重视体现知识的形成过程,而且注意留给学生充分进行自主探索和交流的空间,为教师灵活组织教学提供了清晰的思路。概念的形成没有直接给出结论,而是通过量、算、拼等活动,让学生探索、实验、发现、讨论交流、推理归纳出三角形的内角和是180°。
遵循由特殊到一般的规律进行探究活动是这节课设计的主要特点之一。学生对三角尺上每个角的度数比较熟悉,就从这里入手。先让学生算出每块三角尺三个内角的和是180°,引发学生的猜想:其它三角形的内角和也是180°吗?接着,引导学生小组合作,任意画出不同类型的三角形,用通过量一量、算一算,得出三角形的内角和是180°或接近180°(测量误差),再引导学生通过剪拼的方法发现:各类三角形的三个内角都可以拼成一个平角。再利用课件演示进一步验证,由此获得三角形的内角和是180°的结论。这一系列活动潜移默化地向学生渗透了“转化”数学思想,为后继学习奠定了必要的基础。最后让学生运用结论解决实际问题,练习的安排上,注意练习层次,共安排三个层次,逐步加深。练习形式具有趣味性,激发了学生主动解题的积极性。第一个练习从知识的直接应用到间接应用,数学信息的出现从比较显现到较为隐藏。这些题检测不同层次的学生是否掌握所学知识应该达到的基本要求,顾及到智力水平发展较慢和中等的同学,第3个练习设计了开放性的练习,在小组内完成。由一个同学出题,其它三个同学回答。先给出三角形两个内角的度数,说出另外一个内角。有唯一的答案。训练多次后,只给出三角形一个内角,说出其它两个内角,答案不唯一,可以得出无数个答案。让学生在游戏中消除疲倦激发兴趣,拓展学生思维。兼顾到智力水平发展较快的同学。在整个教学设计中,本着“学贵在思,思源于疑”的思想,不断创设问题情境,让学生去实验、去发现新知识的奥妙,从而让学生在动手操作、积极探索的活动中掌握知识,积累数学活动经验,发展空间观念和推理能力。
这篇教学设计通过施教,符合新课程理念,转变学生的学习方式,能让学生以小组合作的形式进行问题的探索与研究,学生在整节课中学得轻松。整节课的教学设计,条理清晰,层次清楚,学生思维活跃,教学一开始从学生熟悉的三角板抽象出特殊的三角形探讨三角形的内角和是180°,接下来很自然地引导学生探讨所有的三角形的内角和是不是也是180,过渡自然且有吸引力。
在学习活动的过程中,先让学生进行测量、计算,但得不到统一的结果,再引导学生用把三个角拼在一起得到一个平角进行验证。这时,有部分学生在拼凑的过程中出现了困难,花费的时间较长,在这里用课件再演示一遍正好解决了这个问题。练习设计也具有许多优点,注意到练习的梯度,并由浅入深,照顾到不同层次学生的需求,也很有趣味性。但还受课本资源的限制,不能大胆突破教材,充分利用生活资源。例如:可以出示一块被打烂了的三角形玻璃板(如图: ),向学生提出挑战性的问题:老师今天不小心把这块三角形的玻璃板打烂了,要重新买与原来同样大的一块,可老师不知道尺寸,怎么办呢?谁能帮老师解决这个问题呢?让学生利用学过的知识解决生活中常出现的问题,更能使学生体会到数学不仅来源于生活,学习数学的目的更是为了解决生活中的问题,体会到学习数学的重要意义。
一、教学目标:
1.知识与技能:
通过测量、撕拼、折叠等方法,探索和发现三角形三个内角的和等于180°。知道三角形两个角的度数,能求出第三个角的度数。能应用三角形内角和的性质解决一些简单的问题。
2.过程与方法:发展学生动手操作、观察比较和抽象概括的能力。
3.情感、态度与价值观:体验数学活动的探索乐趣,体会研究数学问题的思想方法。
二、课时安排:1课时
三、教学重点:
让学生经历“三角形内角和是180°”这一知识的形成、发展和应用的全过程。
四、教学难点:
能应用三角形的内角和的性质解决一些简单问题。
五、教学过程
(一)导入新课
设疑激趣,现在三角形家族为了一件事正在争论,我们来帮帮它们。(播放课件)
同学们,现在出现了两种不同的意见,有的认为大三角形的内角和大,还有的认为两个三角形的内角和的度数都是一样的。那么到底谁说得对呢
这节课我们就一起来研究这个问题。(板书课题:三角形的内角和)
(二)讲授新课
动手操作,探究新知
1、探究特殊三角形的内角和
师拿出两个三角板,问:它们是什么三角形?
请大家拿出自己的两个三角尺,在小组内说说每一个三角尺上三个角的度数,并求出这两个直角三角形的内角和。
从刚才两个三角形内角和的计算中,你们发现了什么?
2、探究一般三角形内角和
(1)猜一猜。
猜一猜:那么,其它三角形的内角和是多少度呢?(可能是180°)
(2)操作、验证一般三角形内角和是180°。
所有三角形的内角和究竟是不是180°,你能用什么办法来证明,使别人相信呢?
那就请大家在小组共同计算吧!
请每个同学都拿出自己准备的不同的三角形,并量出每个内角的度数,求出它们的内角和,把结果填在表中:
(三)重难点精讲
1.小组汇报结果。
提问:你们发现了什么?
得出三角形的内角和有等于180°的,也有接近180°的。
提出质疑:测量中为什么会出现不同的结果呢?
指名学生说一说:测量有误差。
小结:通过测量计算我们发现每个三角形的三个内角和都在180°左右。
2.继续探究
(1)动手操作,验证猜测。
大家的意见不统一,结论不一样,怎么办?还有其它办法吗?请同学们动脑筋想一想能通过动手操作来验证吗?
(先小组讨论,再汇报方法)
大家的办法都很好,请你们小组合作,动手操作。
(2)学生操作,教师巡视指导。
(3)全班交流汇报验证方法、结果。
学生放在投影仪上展示给大家看。(剪拼、撕拼、折拼)
教师课件展示撕拼法:把三角形的3个内角撕下来,拼成一个大角。得出结论:三角形的内角和是180度。
学生展示不同类型的三角形折成一个平角。
教师课件展示折拼法:把三个内角折叠后拼在一起,(如果学生操作有困难,可以提示学生要点:顶角向下折,折痕要与底边平行,顶点与底边重合,再把剩下的两个角向这个点对折)
引导学生得出结论:三个内角拼在一起也能正好拼成一个平角180°。
小结:刚才同学们通过撕拼法、折拼法得出,无论是什么样的三角形的内角和都是180°(板书)三角形的内角和是180°
辨析概念,透彻理解。
(出示一个大三角形)它的内角和是多少度?
(出示一个很小的三角形 )它的内角和是多少度?
大家可以在小组内用三角尺拼一拼,也可以画一画,互相讨论。
经过一翻激烈的讨论探究后,学生发现: 三角形不论位置、大小、形状如何,它的内角和总是180°
归纳小结
刚才同学们用很多方法证明了什么?现在齐读板书: “三角形的内角和是180°”。
(五)随堂检测
1.猜一猜,可能是什么三角形?
引导学生理解,利用三角形内角和是180度和三角形的分类来解答。
你还能猜出是什么三角形吗?
学生可能会想到,等边三角形每个角都是60度,遮住的是等边三角形。
也可以通过计算解答。
2.引导学生理解,知道每个三角尺的每个角的度数,通过计算得出,每个内角的度数。
了解,四边形的内角和是360度。
3. 让学生动手操作,小组合作。
4. 猜一猜,可能是什么三角形?
第1个,只能是钝角三角形。
第2个,锐角三角形、直角三角形和钝角三角形都有可能。
第3个,只能是锐角三角形。
5.独立完成
小结: 三角形内角和是180 ° 。
六、板书设计
三角形内角和
剪 拼 折
锐角三角形 35°+66°+79°=180°
直角三角形 90°+37°+53°=180°
钝角三角形 112°+35°+32°=179°
三角形的内角和是180°
七、作业布置
完成练一练第7题。
八、教学反思
三角形的内角和是三角形的一个重要特征。本课是安排在学习三角形的概念及分类之后进行的,它是学生以后学习多边形的内角和及解决其它实际问题的基础。学生在掌握知识方面:已经掌握了三角形的分类,比较熟悉平角等有关知识;能力方面:经过三年多的学习,已具备了初步的动手操作能力和主动探究能力以及合作学习的习惯。因此,教材很重视知识的探索与发现,安排了一系列的实验操作活动。教材呈现教学内容时,不但重视体现知识的形成过程,而且注意留给学生充分进行自主探索和交流的空间,为教师灵活组织教学提供了清晰的思路。概念的形成没有直接给出结论,而是通过量、算、拼等活动,让学生探索、实验、发现、讨论交流、推理归纳出三角形的内角和是180°。
遵循由特殊到一般的规律进行探究活动是这节课设计的主要特点之一。学生对三角尺上每个角的度数比较熟悉,就从这里入手。先让学生算出每块三角尺三个内角的和是180°,引发学生的猜想:其它三角形的内角和也是180°吗?接着,引导学生小组合作,任意画出不同类型的三角形,用通过量一量、算一算,得出三角形的内角和是180°或接近180°(测量误差),再引导学生通过剪拼的方法发现:各类三角形的三个内角都可以拼成一个平角。再利用课件演示进一步验证,由此获得三角形的内角和是180°的结论。这一系列活动潜移默化地向学生渗透了“转化”数学思想,为后继学习奠定了必要的基础。最后让学生运用结论解决实际问题,练习的安排上,注意练习层次,共安排三个层次,逐步加深。练习形式具有趣味性,激发了学生主动解题的积极性。第一个练习从知识的直接应用到间接应用,数学信息的出现从比较显现到较为隐藏。这些题检测不同层次的学生是否掌握所学知识应该达到的基本要求,顾及到智力水平发展较慢和中等的同学,第3个练习设计了开放性的练习,在小组内完成。由一个同学出题,其它三个同学回答。先给出三角形两个内角的度数,说出另外一个内角。有唯一的答案。训练多次后,只给出三角形一个内角,说出其它两个内角,答案不唯一,可以得出无数个答案。让学生在游戏中消除疲倦激发兴趣,拓展学生思维。兼顾到智力水平发展较快的同学。在整个教学设计中,本着“学贵在思,思源于疑”的思想,不断创设问题情境,让学生去实验、去发现新知识的奥妙,从而让学生在动手操作、积极探索的活动中掌握知识,积累数学活动经验,发展空间观念和推理能力。
这篇教学设计通过施教,符合新课程理念,转变学生的学习方式,能让学生以小组合作的形式进行问题的探索与研究,学生在整节课中学得轻松。整节课的教学设计,条理清晰,层次清楚,学生思维活跃,教学一开始从学生熟悉的三角板抽象出特殊的三角形探讨三角形的内角和是180°,接下来很自然地引导学生探讨所有的三角形的内角和是不是也是180,过渡自然且有吸引力。
在学习活动的过程中,先让学生进行测量、计算,但得不到统一的结果,再引导学生用把三个角拼在一起得到一个平角进行验证。这时,有部分学生在拼凑的过程中出现了困难,花费的时间较长,在这里用课件再演示一遍正好解决了这个问题。练习设计也具有许多优点,注意到练习的梯度,并由浅入深,照顾到不同层次学生的需求,也很有趣味性。但还受课本资源的限制,不能大胆突破教材,充分利用生活资源。例如:可以出示一块被打烂了的三角形玻璃板(如图: ),向学生提出挑战性的问题:老师今天不小心把这块三角形的玻璃板打烂了,要重新买与原来同样大的一块,可老师不知道尺寸,怎么办呢?谁能帮老师解决这个问题呢?让学生利用学过的知识解决生活中常出现的问题,更能使学生体会到数学不仅来源于生活,学习数学的目的更是为了解决生活中的问题,体会到学习数学的重要意义。
