1.2 函数及其表示(Word含答案)
文档属性
| 名称 | 1.2 函数及其表示(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览


文档简介
1.2 函数及其表示
一、选择题(共10小题;共50分)
1. 函数 的定义域为
A. B.
C. D.
2. 已知实数 ,函数 ,若 ,则 的值为
A. B. C. D.
3. 已知函数 ,若 ,则函数 的解析式为
A. B.
C. D.
4. 下列对应中,是映射的个数为
A. B. C. D.
5. 设 则 等于
A. B. C. D.
6. 已知等腰三角形的周长 为常数,底边长为 ,腰长为 ,则函数 的定义域为
A. B. C. D.
7. 存在函数 满足:对于任意 都有
A. B.
C. D.
8. 如图,长方形 的边 ,, 是 的中点.点 沿着边 , 与 运动,记 .将动点 到 , 两点距离之和表示为 的函数 ,则 的图象大致为
A. B.
C. D.
9. 若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为 ,值域为 的“孪生函数”共有
A. 个 B. 个 C. 个 D. 个
10. 设函数 ,则满足 的 的取值范围是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知函数 ,其中 是 的正比例函数, 是 的反比例函数,且 ,,则 的解析式为 .
12. 已知 是一次函数,且满足 ,则 .
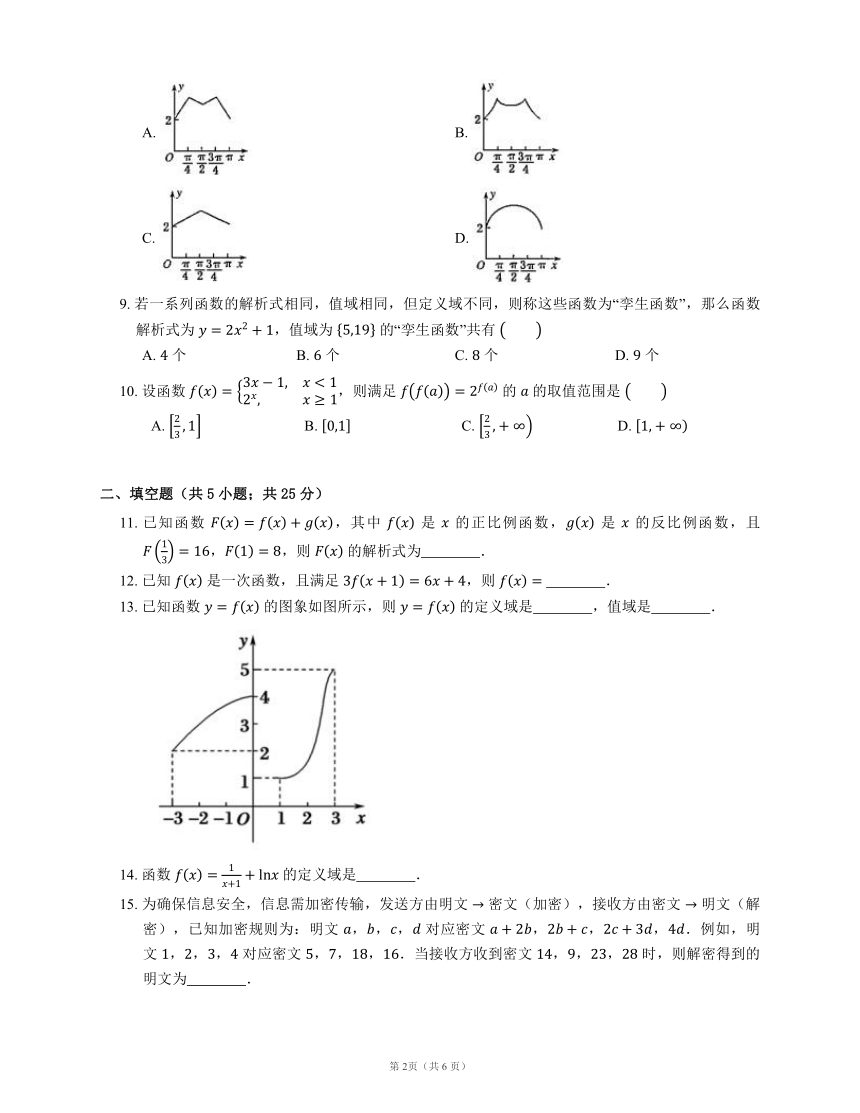
13. 已知函数 的图象如图所示,则 的定义域是 ,值域是 .
14. 函数 的定义域是 .
15. 为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接收方由密文 明文(解密),已知加密规则为:明文 ,,, 对应密文 ,,,.例如,明文 ,,, 对应密文 ,,,.当接收方收到密文 ,,, 时,则解密得到的明文为 .
三、解答题(共3小题;共39分)
16. 已知函数 ,求函数的定义域,并用区间表示.
17. 设集合 是 到 的映射,并满足 .
(1)求 中元素 在 中的原象;
(2)试探索 中有哪些元素在 中存在原象;
(3)求 中元素 在 中有且只有一个原象时 , 所满足的关系式.
18. 已知定义域为 的函数 满足 .
(1)若 ,求 ;又若 ,求 ;
(2)设有且仅有一个实数 ,使得 ,求函数 的解析表达式.
答案
第一部分
1. D 【解析】因为函数 ,所以 ,即 ,
所以 或 ,所以函数的定义域为 .
2. A 【解析】当 时,,则 ,,则 ,
所以 ,则 (舍),
当 时,,则 ,,则 ,
所以 ,解得 .
3. A 【解析】因为 ,所以 ,则 .
4. C 【解析】若在 中的任意一个元素,在 中都有唯一的元素对应,则 到 的对应叫映射,
符合条件,
中, 的元素 不存在对应的元素,不符合条件,
中, 的元素 在 中有两个对应的元素,不符合条件,
故映射的个数为 个.
5. B
【解析】因为 ,所以 .
又 ,所以 .
6. D
7. D 【解析】对于A,令 ,得 ;令 ,得 ,这与函数的定义不符,故A错;
在B中,令 ,得 ;令 ,得 ,与函数的定义不符故B错;
在C中,令 ,得 ;令 ,得 ,与函数的定义不符,故C错;
在D中,变形为 ,令 ,得 ,,从而有 ,显然这个函数关系在定义域 上是成立的.
8. B 【解析】当点 与 , 重合时,易求得 ;当点 为 的中点时,有 ,则 ,易求得 .显然 ,故当 时, 没有取到最大值,则C、D选项错误.当 时,,不是一次函数,排除A.
9. D 【解析】当 时,,解得 ;
当 时,,解得 .
当定义域有两个元素时,有 ,,,,
当定义域有 个元素时,有 ,,,,
当定义域有 个元素时,有 ,所以共有 个.
10. C
【解析】①当 时,,,,显然 .
②当 时,,,,故 .
③当 时,,,,故 .综合①②③知 .
第二部分
11.
12.
13. ,
14.
【解析】由题意得 所以 .
15. ,,,
第三部分
16. 要使函数有意义,应满足
所以 解得 ,且 ,
故函数的定义域为 .
用区间可表示为 .
17. (1) 设 是 中元素 在 中的原象,
于是
解得 或
所以 在 中的原象有两个: 与 .
(2) 设任意 ,则它在 中的原象 应满足:
由 可得 ,将它代入 式并简化得:,
当且仅当 时,方程 有实数解,
因此只有当 中元素 满足 时,在 中才有原象.
(3) 由2的解题过程可知:只有当 中元素 满足 时,它在 中且只有一个原象.
18. (1) 因为对 ,有 ,
所以 ,
又由 得 ,即 ,
若 ,则 ,即 ;
(2) 因为对 ,有 ,
又因为有且仅有一个实数 ,使得 ,
所以对 ,有 ,令 ,则 ,
又因为 ,
所以 ,故 或 ,
若 ,则 ,即 ,
但方程 有两个不相等的实数根,与题设条件矛盾,故 ,
若 ,则 ,即 ,易验证该函数满足题设条件,
综上,所求函数为 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 函数 的定义域为
A. B.
C. D.
2. 已知实数 ,函数 ,若 ,则 的值为
A. B. C. D.
3. 已知函数 ,若 ,则函数 的解析式为
A. B.
C. D.
4. 下列对应中,是映射的个数为
A. B. C. D.
5. 设 则 等于
A. B. C. D.
6. 已知等腰三角形的周长 为常数,底边长为 ,腰长为 ,则函数 的定义域为
A. B. C. D.
7. 存在函数 满足:对于任意 都有
A. B.
C. D.
8. 如图,长方形 的边 ,, 是 的中点.点 沿着边 , 与 运动,记 .将动点 到 , 两点距离之和表示为 的函数 ,则 的图象大致为
A. B.
C. D.
9. 若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为 ,值域为 的“孪生函数”共有
A. 个 B. 个 C. 个 D. 个
10. 设函数 ,则满足 的 的取值范围是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知函数 ,其中 是 的正比例函数, 是 的反比例函数,且 ,,则 的解析式为 .
12. 已知 是一次函数,且满足 ,则 .
13. 已知函数 的图象如图所示,则 的定义域是 ,值域是 .
14. 函数 的定义域是 .
15. 为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接收方由密文 明文(解密),已知加密规则为:明文 ,,, 对应密文 ,,,.例如,明文 ,,, 对应密文 ,,,.当接收方收到密文 ,,, 时,则解密得到的明文为 .
三、解答题(共3小题;共39分)
16. 已知函数 ,求函数的定义域,并用区间表示.
17. 设集合 是 到 的映射,并满足 .
(1)求 中元素 在 中的原象;
(2)试探索 中有哪些元素在 中存在原象;
(3)求 中元素 在 中有且只有一个原象时 , 所满足的关系式.
18. 已知定义域为 的函数 满足 .
(1)若 ,求 ;又若 ,求 ;
(2)设有且仅有一个实数 ,使得 ,求函数 的解析表达式.
答案
第一部分
1. D 【解析】因为函数 ,所以 ,即 ,
所以 或 ,所以函数的定义域为 .
2. A 【解析】当 时,,则 ,,则 ,
所以 ,则 (舍),
当 时,,则 ,,则 ,
所以 ,解得 .
3. A 【解析】因为 ,所以 ,则 .
4. C 【解析】若在 中的任意一个元素,在 中都有唯一的元素对应,则 到 的对应叫映射,
符合条件,
中, 的元素 不存在对应的元素,不符合条件,
中, 的元素 在 中有两个对应的元素,不符合条件,
故映射的个数为 个.
5. B
【解析】因为 ,所以 .
又 ,所以 .
6. D
7. D 【解析】对于A,令 ,得 ;令 ,得 ,这与函数的定义不符,故A错;
在B中,令 ,得 ;令 ,得 ,与函数的定义不符故B错;
在C中,令 ,得 ;令 ,得 ,与函数的定义不符,故C错;
在D中,变形为 ,令 ,得 ,,从而有 ,显然这个函数关系在定义域 上是成立的.
8. B 【解析】当点 与 , 重合时,易求得 ;当点 为 的中点时,有 ,则 ,易求得 .显然 ,故当 时, 没有取到最大值,则C、D选项错误.当 时,,不是一次函数,排除A.
9. D 【解析】当 时,,解得 ;
当 时,,解得 .
当定义域有两个元素时,有 ,,,,
当定义域有 个元素时,有 ,,,,
当定义域有 个元素时,有 ,所以共有 个.
10. C
【解析】①当 时,,,,显然 .
②当 时,,,,故 .
③当 时,,,,故 .综合①②③知 .
第二部分
11.
12.
13. ,
14.
【解析】由题意得 所以 .
15. ,,,
第三部分
16. 要使函数有意义,应满足
所以 解得 ,且 ,
故函数的定义域为 .
用区间可表示为 .
17. (1) 设 是 中元素 在 中的原象,
于是
解得 或
所以 在 中的原象有两个: 与 .
(2) 设任意 ,则它在 中的原象 应满足:
由 可得 ,将它代入 式并简化得:,
当且仅当 时,方程 有实数解,
因此只有当 中元素 满足 时,在 中才有原象.
(3) 由2的解题过程可知:只有当 中元素 满足 时,它在 中且只有一个原象.
18. (1) 因为对 ,有 ,
所以 ,
又由 得 ,即 ,
若 ,则 ,即 ;
(2) 因为对 ,有 ,
又因为有且仅有一个实数 ,使得 ,
所以对 ,有 ,令 ,则 ,
又因为 ,
所以 ,故 或 ,
若 ,则 ,即 ,
但方程 有两个不相等的实数根,与题设条件矛盾,故 ,
若 ,则 ,即 ,易验证该函数满足题设条件,
综上,所求函数为 .
第1页(共1 页)
