高中数学人教新课标A版必修1 2.3 幂函数(word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版必修1 2.3 幂函数(word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 351.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 15:04:30 | ||
图片预览



文档简介
2.3 幂函数
一、选择题(共10小题;共50分)
1. 如图是幂函数 的部分图象,已知 取 ,,, 这四个值,则与曲线 ,,, 相对应的 依次为
A. ,,, B. ,,,
C. ,,, D. ,,,
2. 幂函数 的图象经过点 ,则
A. 是偶函数,且在 上单调递增
B. 是偶函数,且在 上单调递减
C. 是奇函数,且在 上单调递减
D. 既不是奇函数,也不是偶函数,在 上单调递增
3. 幂函数 ,当 取不同的正数时,在区间 上它们的图象是一族美丽的曲线(如图).设点 ,,连接 ,线段 恰好被其中的两个幂函数 , 的图象三等分,即有 .那么,
A. B. C. D. 无法确定
4. 函数 的大致图象是
A. B.
C. D.
5. 幂函数的图象经过点 ,若 ,则下列各式正确的是
A.
B.
C.
D.
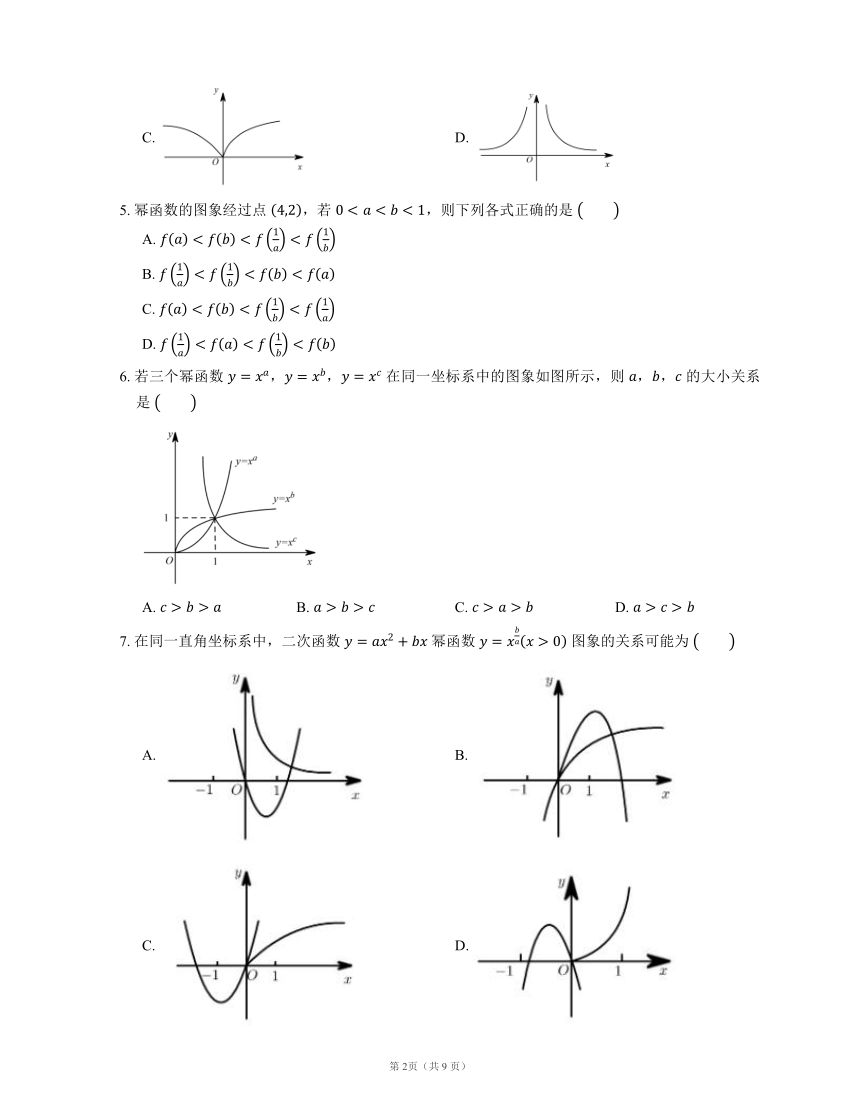
6. 若三个幂函数 ,, 在同一坐标系中的图象如图所示,则 ,, 的大小关系是
A. B. C. D.
7. 在同一直角坐标系中,二次函数 幂函数 图象的关系可能为
A. B.
C. D.
8. 若 是幂函数,且满足 ,则
A. B. C. D.
9. ,, 的大小顺序为
A. B.
C. D.
10. 设 是定义在 上的函数若存在两个不等实数 ,使得 ,则称函数 具有性质 ,那么下列函数:;;;.
不具有性质 的函数为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知幂函数 的图象过点 ,则 .
12. 已知幂函数 的图象过点 ,则 .
13. 若函数 是幂函数,且 ,则 .
14. 已知函数 ,,函数 ,.若对任意 ,总存在 ,使 成立.则实数 的取值范围是 .
15. 已知函数 ,给出下列命题:
①若 ,则 ;
②若 ,则 ;
③若 ,则 ;
④若 ,则 .
其中,所有正确命题的序号是 .
三、解答题(共3小题;共39分)
16. 已知函数 为何值时,函数 是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
17. 如图,幂函数 的图象关于 轴对称,且与 轴, 轴均无交点,求此函数的解析式及不等式 的解集.
18. 讨论函数 的定义域、奇偶性和单调性.
答案
第一部分
1. A 【解析】方法一:
曲线 , 过点 ,,且在第一象限内为增函数,
所以 , 为 ,,
显然 对应 , 对应 ., 过点 ,且在第一象限内为减函数,
所以 , 为 ,,
显然 对应 , 对应 .
方法二:
取 ,分别代入 ,,,,
可求得 ,,,,
比较得 ,
则与曲线 ,,, 相对应的 依次为 ,,,.
2. D 【解析】由题意设 ,
因为函数 的图象经过点 ,
所以 ,
解得 ,即 ,
所以 既不是奇函数,也不是偶函数,且在 上是增函数,
故选D.
3. A 【解析】由题意可得:,.
即 ,.
所以 .
4. A 【解析】因为 ,所以 在 上单调递减,排除选项B,C;
又 的定义域为 ,故排除选项D.
5. C
【解析】设幂函数为 ,将 代入得 ,
所以 ,该函数在 上为增函数,又 ,
所以 ,即 ,
所以 .
6. B 【解析】幂函数 的图象在直线 的右侧部分,自下而上, 的值逐渐增大.
7. A 【解析】A选项:二次函数 开口向上,
则 ,其对称轴为 ,
幂函数 中,,为减函数,符合题意,故A正确;
B选项:二次函数 开口向下,
则 ,其对称轴为 ,
幂函数 中,,为减函数,不符合题意,故B错误;
C选项:二次函数 开口向上,
则 ,其对称轴为 ,
幂函数 中,,为增函数,
且其增加越来越快,不符合题意,故C错误;
D选项:二次函数 开口向下,
则 ,其对称轴为 ,
幂函数 中,,为增函数,
且其增加越来越慢,不符合题意,故D错误.
8. D 【解析】设 ,则 ,.
因为 ,
所以 ,
所以 ,
所以 .
9. B
10. D
【解析】 选择的两点关于原点对称即可,如图(),, 满足;
同 ,选择的两点关于原点对称即可,如图();
如图, 与 的交点满足题意,当然,其他点对也有满足;
没有满足的点对,
证明:假设存在 ,使得:,即:,
又 ,故不存在.
第二部分
11.
【解析】由题意令 ,由于图象过点 ,
得 ,,
所以 ,
所以 .
12.
【解析】设幂函数 ,由函数图象过点 ,
所以 ,解得 ,
所以 ,
所以 .
13.
14.
【解析】对任意 ,总存在 ,使 成立,则可得出函数 的值域是函数 值域的子集,函数 的值域为 .当 时,显然不合题意,当 时,函数 的值域是 ,当 时,函数 的值域是 ,所以
解得实数 的取值范围是 .
15. ①④
【解析】①由幂函数的性质知 时,,故①正确;
② 如图, 时, 表示曲线 上两点连线的斜率,显然存在 的情况,即 ,也即 ,故② 错;
③ 如图, 表示曲线 上的点 与原点连线的斜率,当 增大时, 在减小,即 时,,即 ,故③ 错;
④ 如图,对于 ,则 两点的纵坐标分别为 ,显然 ,故④正确.
第三部分
16. (1)若 为正比例函数,则 .
(2)若 为反比例函数,则 .
(3)若 为二次函数,则 .
(4)若 为幂函数,则 ,所以 .
17. 由题意,得 ,所以 .
因为 ,所以 .
因为幂函数的图象关于 轴对称,
所以 为偶数,
因为 时,,
时,,,.
故当 时, 符合题意,即 .
所以不等式 即 ,即 ,
结合图象单调性可得 ,解得 或 .故不等式解集为 .
18. ①因为 是正偶数,所以 是正奇数.
所以,函数 的定义域为 .
②因为 是正奇数,所以
且定义域关于原点对称.所以 是 上的奇函数.
③因为 ,且 是正奇数,所以,函数 在 上单调递增.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 如图是幂函数 的部分图象,已知 取 ,,, 这四个值,则与曲线 ,,, 相对应的 依次为
A. ,,, B. ,,,
C. ,,, D. ,,,
2. 幂函数 的图象经过点 ,则
A. 是偶函数,且在 上单调递增
B. 是偶函数,且在 上单调递减
C. 是奇函数,且在 上单调递减
D. 既不是奇函数,也不是偶函数,在 上单调递增
3. 幂函数 ,当 取不同的正数时,在区间 上它们的图象是一族美丽的曲线(如图).设点 ,,连接 ,线段 恰好被其中的两个幂函数 , 的图象三等分,即有 .那么,
A. B. C. D. 无法确定
4. 函数 的大致图象是
A. B.
C. D.
5. 幂函数的图象经过点 ,若 ,则下列各式正确的是
A.
B.
C.
D.
6. 若三个幂函数 ,, 在同一坐标系中的图象如图所示,则 ,, 的大小关系是
A. B. C. D.
7. 在同一直角坐标系中,二次函数 幂函数 图象的关系可能为
A. B.
C. D.
8. 若 是幂函数,且满足 ,则
A. B. C. D.
9. ,, 的大小顺序为
A. B.
C. D.
10. 设 是定义在 上的函数若存在两个不等实数 ,使得 ,则称函数 具有性质 ,那么下列函数:;;;.
不具有性质 的函数为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知幂函数 的图象过点 ,则 .
12. 已知幂函数 的图象过点 ,则 .
13. 若函数 是幂函数,且 ,则 .
14. 已知函数 ,,函数 ,.若对任意 ,总存在 ,使 成立.则实数 的取值范围是 .
15. 已知函数 ,给出下列命题:
①若 ,则 ;
②若 ,则 ;
③若 ,则 ;
④若 ,则 .
其中,所有正确命题的序号是 .
三、解答题(共3小题;共39分)
16. 已知函数 为何值时,函数 是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
17. 如图,幂函数 的图象关于 轴对称,且与 轴, 轴均无交点,求此函数的解析式及不等式 的解集.
18. 讨论函数 的定义域、奇偶性和单调性.
答案
第一部分
1. A 【解析】方法一:
曲线 , 过点 ,,且在第一象限内为增函数,
所以 , 为 ,,
显然 对应 , 对应 ., 过点 ,且在第一象限内为减函数,
所以 , 为 ,,
显然 对应 , 对应 .
方法二:
取 ,分别代入 ,,,,
可求得 ,,,,
比较得 ,
则与曲线 ,,, 相对应的 依次为 ,,,.
2. D 【解析】由题意设 ,
因为函数 的图象经过点 ,
所以 ,
解得 ,即 ,
所以 既不是奇函数,也不是偶函数,且在 上是增函数,
故选D.
3. A 【解析】由题意可得:,.
即 ,.
所以 .
4. A 【解析】因为 ,所以 在 上单调递减,排除选项B,C;
又 的定义域为 ,故排除选项D.
5. C
【解析】设幂函数为 ,将 代入得 ,
所以 ,该函数在 上为增函数,又 ,
所以 ,即 ,
所以 .
6. B 【解析】幂函数 的图象在直线 的右侧部分,自下而上, 的值逐渐增大.
7. A 【解析】A选项:二次函数 开口向上,
则 ,其对称轴为 ,
幂函数 中,,为减函数,符合题意,故A正确;
B选项:二次函数 开口向下,
则 ,其对称轴为 ,
幂函数 中,,为减函数,不符合题意,故B错误;
C选项:二次函数 开口向上,
则 ,其对称轴为 ,
幂函数 中,,为增函数,
且其增加越来越快,不符合题意,故C错误;
D选项:二次函数 开口向下,
则 ,其对称轴为 ,
幂函数 中,,为增函数,
且其增加越来越慢,不符合题意,故D错误.
8. D 【解析】设 ,则 ,.
因为 ,
所以 ,
所以 ,
所以 .
9. B
10. D
【解析】 选择的两点关于原点对称即可,如图(),, 满足;
同 ,选择的两点关于原点对称即可,如图();
如图, 与 的交点满足题意,当然,其他点对也有满足;
没有满足的点对,
证明:假设存在 ,使得:,即:,
又 ,故不存在.
第二部分
11.
【解析】由题意令 ,由于图象过点 ,
得 ,,
所以 ,
所以 .
12.
【解析】设幂函数 ,由函数图象过点 ,
所以 ,解得 ,
所以 ,
所以 .
13.
14.
【解析】对任意 ,总存在 ,使 成立,则可得出函数 的值域是函数 值域的子集,函数 的值域为 .当 时,显然不合题意,当 时,函数 的值域是 ,当 时,函数 的值域是 ,所以
解得实数 的取值范围是 .
15. ①④
【解析】①由幂函数的性质知 时,,故①正确;
② 如图, 时, 表示曲线 上两点连线的斜率,显然存在 的情况,即 ,也即 ,故② 错;
③ 如图, 表示曲线 上的点 与原点连线的斜率,当 增大时, 在减小,即 时,,即 ,故③ 错;
④ 如图,对于 ,则 两点的纵坐标分别为 ,显然 ,故④正确.
第三部分
16. (1)若 为正比例函数,则 .
(2)若 为反比例函数,则 .
(3)若 为二次函数,则 .
(4)若 为幂函数,则 ,所以 .
17. 由题意,得 ,所以 .
因为 ,所以 .
因为幂函数的图象关于 轴对称,
所以 为偶数,
因为 时,,
时,,,.
故当 时, 符合题意,即 .
所以不等式 即 ,即 ,
结合图象单调性可得 ,解得 或 .故不等式解集为 .
18. ①因为 是正偶数,所以 是正奇数.
所以,函数 的定义域为 .
②因为 是正奇数,所以
且定义域关于原点对称.所以 是 上的奇函数.
③因为 ,且 是正奇数,所以,函数 在 上单调递增.
第1页(共1 页)
