高中数学人教新课标A版必修1 3.2 函数模型及其应用 (word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版必修1 3.2 函数模型及其应用 (word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 190.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 15:13:44 | ||
图片预览

文档简介
3.2 函数模型及其应用
一、选择题(共10小题;共50分)
1. 某种动物繁殖数量 (单位:只)与时间 (单位:年)的关系为 ,设这种动物第一年有 只,第 年它们发展到
A. 只 B. 只 C. 只 D. 只
2. 基本再生数 与世代间隔 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数 随时间 (单位:天)的变化规律,指数增长率 与 , 近似满足 .有学者基于已有数据估计出 , .据此,在新冠肺炎疫情初始阶段,累计感染病例数增加 倍需要的时间约为
A. 天 B. 天 C. 天 D. 天
3. Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 ( 的单位:天)的Logistic模型:,其中 为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为
A. B. C. D.
4. 某市家庭煤气的使用量 和煤气费 (元)满足关系 ,已知某家庭 年前三个月的煤气费如表:
若四月份该家庭使用了 的煤气,则其煤气费为
A. 元 B. 元 C. 元 D. 元
5. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过 立方米的,按每立方米 元收费;用水量超过 立方米的,超过部分按每立方米 元收费.某职工某月缴水费 元,则该职工这个月实际用水量为
A. 立方米 B. 立方米 C. 立方米 D. 立方米
6. 某市家庭煤气的使用量 和煤气费 (元)满足 ,已知某家庭 年前三个月的煤气费如表,若四月份该家庭使用了 的煤气,则其煤气费为
A. 元 B. 元 C. 元 D. 元
7. 某同学参加研究性学习活动,得到如下实验数据:
现欲从理论上对这些数据进行分析并预测,则下列模拟函数合适的是
A. B. C. D.
8. 在一定的储存温度范围内,某食品的保鲜时间 (单位:小时)与储存温度 (单位:)满足函数关系 ( 为自然对数的底数,, 为常数),若该食品在 时的保鲜时间为 小时,在 时的保鲜时间为 小时,则该食品在 时的保鲜时间为
A. 小时 B. 小时 C. 小时 D. 小时
9. 根据统计,一名工人组装第 件某产品所用的时间(单位:分钟)为 (, 为常数),已知工人组装第 件产品用时 ,组装第 件产品用时 ,那么 和 的值分别是
A. , B. , C. , D. ,
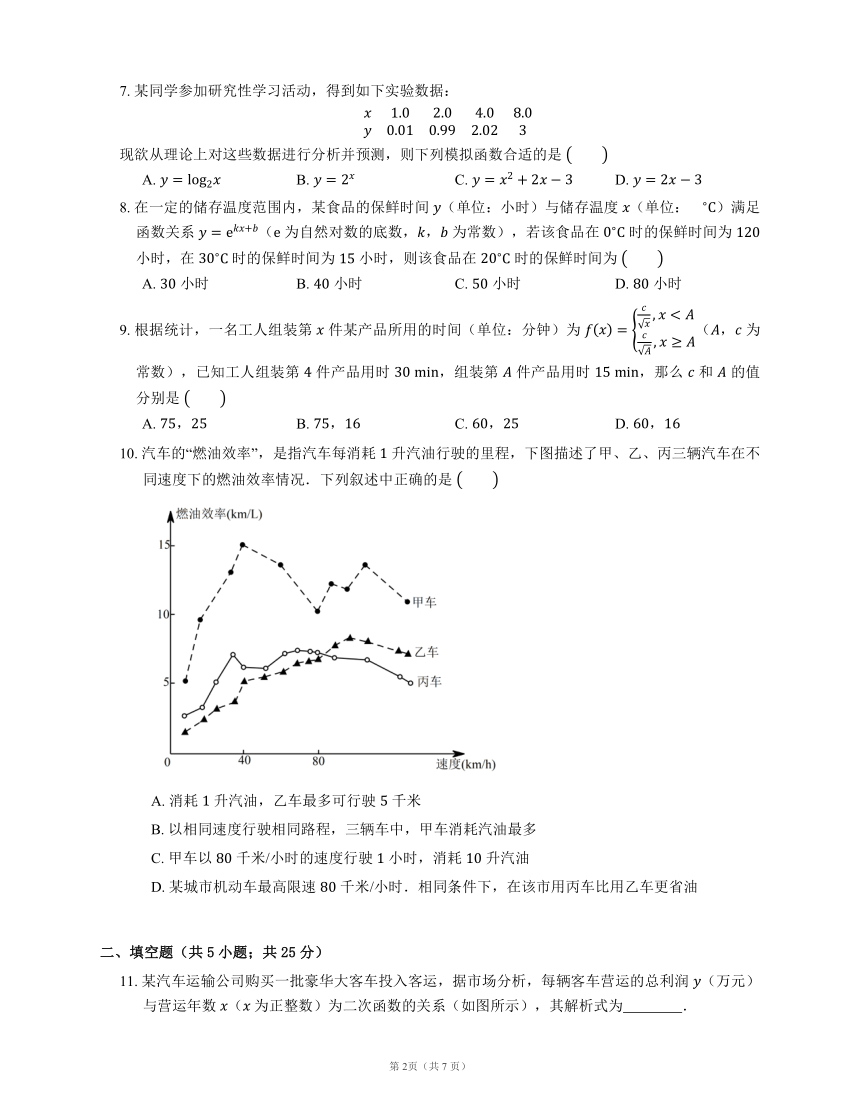
10. 汽车的“燃油效率”,是指汽车每消耗 升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是
A. 消耗 升汽油,乙车最多可行驶 千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以 千米/小时的速度行驶 小时,消耗 升汽油
D. 某城市机动车最高限速 千米/小时.相同条件下,在该市用丙车比用乙车更省油
二、填空题(共5小题;共25分)
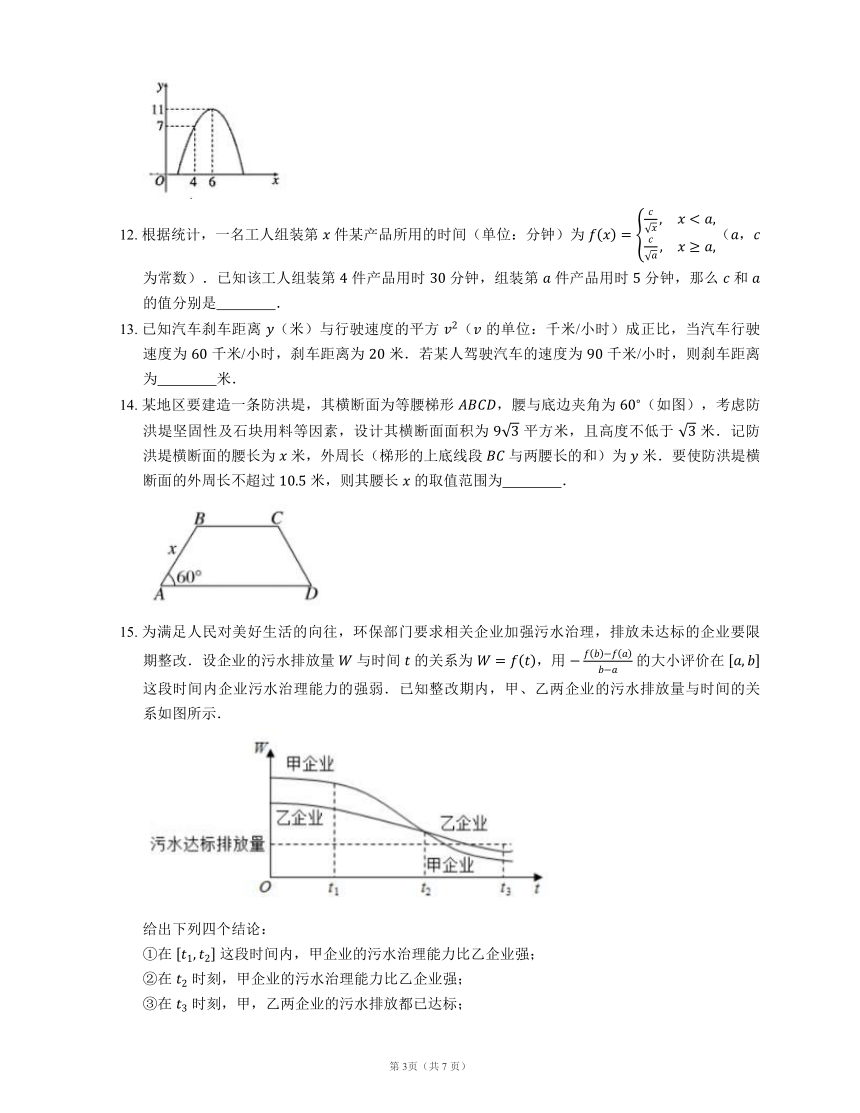
11. 某汽车运输公司购买一批豪华大客车投入客运,据市场分析,每辆客车营运的总利润 (万元)与营运年数 ( 为正整数)为二次函数的关系(如图所示),其解析式为 .
12. 根据统计,一名工人组装第 件某产品所用的时间(单位:分钟)为 (, 为常数).已知该工人组装第 件产品用时 分钟,组装第 件产品用时 分钟,那么 和 的值分别是 .
13. 已知汽车刹车距离 (米)与行驶速度的平方 ( 的单位:千米/小时)成正比,当汽车行驶速度为 千米/小时,刹车距离为 米.若某人驾驶汽车的速度为 千米/小时,则刹车距离为 米.
14. 某地区要建造一条防洪堤,其横断面为等腰梯形 ,腰与底边夹角为 (如图),考虑防洪堤坚固性及石块用料等因素,设计其横断面面积为 平方米,且高度不低于 米.记防洪堤横断面的腰长为 米,外周长(梯形的上底线段 与两腰长的和)为 米.要使防洪堤横断面的外周长不超过 米,则其腰长 的取值范围为 .
15. 为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量 与时间 的关系为 ,用 的大小评价在 这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在 这段时间内,甲企业的污水治理能力比乙企业强;
②在 时刻,甲企业的污水治理能力比乙企业强;
③在 时刻,甲,乙两企业的污水排放都已达标;
④甲企业在 ,, 这三段时间中,在 的污水治理能力最强.
其中所有正确结论的序号是 .
三、解答题(共3小题;共39分)
16. 长为 的铁丝弯成下部为矩形、上部为半圆形的框架(如图所示),若矩形底边长为 ,求此框架围成图形的面积 关于 的函数.
17. 银行一年期定期储蓄的年利率为 ,如果存款到期不取继续存于银行,银行自动将本金及利息转存一年期定期储蓄.
(1)某人以一年期定期储蓄存入银行 万元,问: 年后,这笔钱款的本利和为多少 (精确到 元)
(2)设本金为 元,年利率为 ,本利和为 ,写出 随存入年数 变化的函数表达式.
18. 某质点在 内运动速度 是时间 的函数,它的图象如图所示.用解析法表示这个函数,并求出 时质点的速度.
答案
第一部分
1. A 【解析】当 时,,得 ,
故当 时,.
2. B 【解析】【解析】因为 ,,,所以 ,所以 ,
设在新冠肺炎疫情初始阶段,累计感染病例数增加 倍需要的时间为 天,则 ,所以 ,所以 ,
所以 天.
3. C 【解析】因为 ,
所以 ,则 ,
所以 ,解得 .
4. A
5. A
6. A 【解析】依题意有
解得 ,,.
所以 .
所以 (元),
即四月份议家庭的煤气费为 元.
7. A 【解析】根据题中数据画出散点图,如图所示.
由图可知上述散点大体分布在函数 的图象附近,故函数 可以近似地反映这些数据的规律.故选A.
8. A
9. D
10. D
【解析】乙车的燃油效率可以大于 ,即消耗 升汽油可以行驶大于 千米的路程,故A错误;以相同的速度行驶相同的里程,甲车的燃油消耗率最高,因此以相同的的速度行驶相同的里程,甲车的消耗汽油最少,B错误;甲车以 千米/小时的速度行驶时燃油效率为 千米/升,行驶 小时,里程为 千米,消耗 升汽油,故C错误;最高限速 千米/小时,丙车的燃油效率比乙车高,因此在相同的条件下,在该市用丙车比用乙车更省油,所以D正确.
第二部分
11. ,
【解析】设 ,“,过点 ,
所以 ,解得 ,
所以 ,.
12. ,
【解析】显然 ,
则由题意可得
解得
13.
【解析】由汽车刹车距离 (米)与行驶速度的平方 ( 的单位:千米/小时)成正比,设 ,
当汽车行驶速度为 千米/小时,刹车距离为 米,
所以 ,
解得 ,
所以 .
当 千米/小时,(米).
14.
15. ①②③
【解析】设甲企业的污水排放量 与时间 的关系为 ,乙企业的污水排放量 与时间 的关系为 .
对于①,在 这段时间内,甲企业的污水治理能力为 ,乙企业的污水治理能力为 .
由图可知,,所以 ,
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知, 在 时刻的切线的斜率小于 在 时刻的切线的斜率,但两切线斜率均为负值,
所以在 时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在 时刻,甲,乙两企业的污水排放都小于污水达标排放量,
所以在 时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在 ,, 这三段时间中,在 的污水治理能力最强,故④错误.
所以正确结论的序号是①②③.
第三部分
16. 由题意知 ,,于是 ,
所以 .
又 解得 .
所以此函数的定义域为 .
故所求的函数为 ().
17. (1) 年后的本利和为 ;
年后的本利和为 ;
年后的本利和为 .
所以, 年后的本利和为 元.
(2) 由()的计算得: 随存入年数 变化的函数表达式为 .
18. 根据图象可得函数的表达式为 ,
当 时,.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 某种动物繁殖数量 (单位:只)与时间 (单位:年)的关系为 ,设这种动物第一年有 只,第 年它们发展到
A. 只 B. 只 C. 只 D. 只
2. 基本再生数 与世代间隔 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数 随时间 (单位:天)的变化规律,指数增长率 与 , 近似满足 .有学者基于已有数据估计出 , .据此,在新冠肺炎疫情初始阶段,累计感染病例数增加 倍需要的时间约为
A. 天 B. 天 C. 天 D. 天
3. Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 ( 的单位:天)的Logistic模型:,其中 为最大确诊病例数.当 时,标志着已初步遏制疫情,则 约为
A. B. C. D.
4. 某市家庭煤气的使用量 和煤气费 (元)满足关系 ,已知某家庭 年前三个月的煤气费如表:
若四月份该家庭使用了 的煤气,则其煤气费为
A. 元 B. 元 C. 元 D. 元
5. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过 立方米的,按每立方米 元收费;用水量超过 立方米的,超过部分按每立方米 元收费.某职工某月缴水费 元,则该职工这个月实际用水量为
A. 立方米 B. 立方米 C. 立方米 D. 立方米
6. 某市家庭煤气的使用量 和煤气费 (元)满足 ,已知某家庭 年前三个月的煤气费如表,若四月份该家庭使用了 的煤气,则其煤气费为
A. 元 B. 元 C. 元 D. 元
7. 某同学参加研究性学习活动,得到如下实验数据:
现欲从理论上对这些数据进行分析并预测,则下列模拟函数合适的是
A. B. C. D.
8. 在一定的储存温度范围内,某食品的保鲜时间 (单位:小时)与储存温度 (单位:)满足函数关系 ( 为自然对数的底数,, 为常数),若该食品在 时的保鲜时间为 小时,在 时的保鲜时间为 小时,则该食品在 时的保鲜时间为
A. 小时 B. 小时 C. 小时 D. 小时
9. 根据统计,一名工人组装第 件某产品所用的时间(单位:分钟)为 (, 为常数),已知工人组装第 件产品用时 ,组装第 件产品用时 ,那么 和 的值分别是
A. , B. , C. , D. ,
10. 汽车的“燃油效率”,是指汽车每消耗 升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是
A. 消耗 升汽油,乙车最多可行驶 千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以 千米/小时的速度行驶 小时,消耗 升汽油
D. 某城市机动车最高限速 千米/小时.相同条件下,在该市用丙车比用乙车更省油
二、填空题(共5小题;共25分)
11. 某汽车运输公司购买一批豪华大客车投入客运,据市场分析,每辆客车营运的总利润 (万元)与营运年数 ( 为正整数)为二次函数的关系(如图所示),其解析式为 .
12. 根据统计,一名工人组装第 件某产品所用的时间(单位:分钟)为 (, 为常数).已知该工人组装第 件产品用时 分钟,组装第 件产品用时 分钟,那么 和 的值分别是 .
13. 已知汽车刹车距离 (米)与行驶速度的平方 ( 的单位:千米/小时)成正比,当汽车行驶速度为 千米/小时,刹车距离为 米.若某人驾驶汽车的速度为 千米/小时,则刹车距离为 米.
14. 某地区要建造一条防洪堤,其横断面为等腰梯形 ,腰与底边夹角为 (如图),考虑防洪堤坚固性及石块用料等因素,设计其横断面面积为 平方米,且高度不低于 米.记防洪堤横断面的腰长为 米,外周长(梯形的上底线段 与两腰长的和)为 米.要使防洪堤横断面的外周长不超过 米,则其腰长 的取值范围为 .
15. 为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改.设企业的污水排放量 与时间 的关系为 ,用 的大小评价在 这段时间内企业污水治理能力的强弱.已知整改期内,甲、乙两企业的污水排放量与时间的关系如图所示.
给出下列四个结论:
①在 这段时间内,甲企业的污水治理能力比乙企业强;
②在 时刻,甲企业的污水治理能力比乙企业强;
③在 时刻,甲,乙两企业的污水排放都已达标;
④甲企业在 ,, 这三段时间中,在 的污水治理能力最强.
其中所有正确结论的序号是 .
三、解答题(共3小题;共39分)
16. 长为 的铁丝弯成下部为矩形、上部为半圆形的框架(如图所示),若矩形底边长为 ,求此框架围成图形的面积 关于 的函数.
17. 银行一年期定期储蓄的年利率为 ,如果存款到期不取继续存于银行,银行自动将本金及利息转存一年期定期储蓄.
(1)某人以一年期定期储蓄存入银行 万元,问: 年后,这笔钱款的本利和为多少 (精确到 元)
(2)设本金为 元,年利率为 ,本利和为 ,写出 随存入年数 变化的函数表达式.
18. 某质点在 内运动速度 是时间 的函数,它的图象如图所示.用解析法表示这个函数,并求出 时质点的速度.
答案
第一部分
1. A 【解析】当 时,,得 ,
故当 时,.
2. B 【解析】【解析】因为 ,,,所以 ,所以 ,
设在新冠肺炎疫情初始阶段,累计感染病例数增加 倍需要的时间为 天,则 ,所以 ,所以 ,
所以 天.
3. C 【解析】因为 ,
所以 ,则 ,
所以 ,解得 .
4. A
5. A
6. A 【解析】依题意有
解得 ,,.
所以 .
所以 (元),
即四月份议家庭的煤气费为 元.
7. A 【解析】根据题中数据画出散点图,如图所示.
由图可知上述散点大体分布在函数 的图象附近,故函数 可以近似地反映这些数据的规律.故选A.
8. A
9. D
10. D
【解析】乙车的燃油效率可以大于 ,即消耗 升汽油可以行驶大于 千米的路程,故A错误;以相同的速度行驶相同的里程,甲车的燃油消耗率最高,因此以相同的的速度行驶相同的里程,甲车的消耗汽油最少,B错误;甲车以 千米/小时的速度行驶时燃油效率为 千米/升,行驶 小时,里程为 千米,消耗 升汽油,故C错误;最高限速 千米/小时,丙车的燃油效率比乙车高,因此在相同的条件下,在该市用丙车比用乙车更省油,所以D正确.
第二部分
11. ,
【解析】设 ,“,过点 ,
所以 ,解得 ,
所以 ,.
12. ,
【解析】显然 ,
则由题意可得
解得
13.
【解析】由汽车刹车距离 (米)与行驶速度的平方 ( 的单位:千米/小时)成正比,设 ,
当汽车行驶速度为 千米/小时,刹车距离为 米,
所以 ,
解得 ,
所以 .
当 千米/小时,(米).
14.
15. ①②③
【解析】设甲企业的污水排放量 与时间 的关系为 ,乙企业的污水排放量 与时间 的关系为 .
对于①,在 这段时间内,甲企业的污水治理能力为 ,乙企业的污水治理能力为 .
由图可知,,所以 ,
即甲企业的污水治理能力比乙企业强,故①正确;
对于②,由图可知, 在 时刻的切线的斜率小于 在 时刻的切线的斜率,但两切线斜率均为负值,
所以在 时刻,甲企业的污水治理能力比乙企业强,故②正确;
对于③,在 时刻,甲,乙两企业的污水排放都小于污水达标排放量,
所以在 时刻,甲,乙两企业的污水排放都已达标,故③正确;
对于④,由图可知,甲企业在 ,, 这三段时间中,在 的污水治理能力最强,故④错误.
所以正确结论的序号是①②③.
第三部分
16. 由题意知 ,,于是 ,
所以 .
又 解得 .
所以此函数的定义域为 .
故所求的函数为 ().
17. (1) 年后的本利和为 ;
年后的本利和为 ;
年后的本利和为 .
所以, 年后的本利和为 元.
(2) 由()的计算得: 随存入年数 变化的函数表达式为 .
18. 根据图象可得函数的表达式为 ,
当 时,.
第1页(共1 页)
