人教版数学七年级下册 9.1.2不等式的基本性质 课件(共18张PPT)
文档属性
| 名称 | 人教版数学七年级下册 9.1.2不等式的基本性质 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 862.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 16:50:26 | ||
图片预览





文档简介
(共18张PPT)
“<”(或“≤”),“>”(或“≥”)
1、不等式
2、理解关键词意义
非负数
不小于
不大于
非正数
至少(最少)
不超过
>
<
<
1、用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3
1、观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
同一个整式
等式的两边都加上(或减去) 或 ,所得的结果仍是等式。
等式的基本性质1:
2、继续观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
等式的两边都乘以(或除以) (除数不能为零),所得的结果仍是等式。
等式的基本性质2:
那么不等式有没有类似的性质呢?
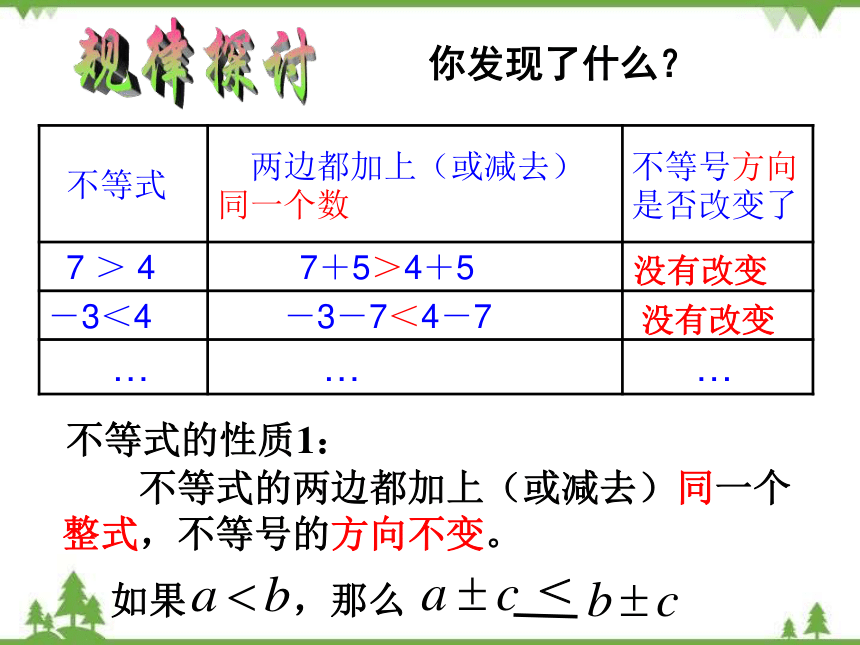
不等式 两边都加上(或减去)同一个数 不等号方向是否改变了
7 > 4 7+5>4+5
-3<4 -3-7<4-7
… … …
不等式的性质1:
不等式的两边都加上(或减去)同一个整式,不等号的方向不变。
如果 ,那么
<
没有改变
没有改变
你发现了什么?
完成下列填空:
2<3 2X5 ____ 3X5
2<3 2X.05 ____3X0.5
2<3 2X(-1)____3X(-1)
2<3 2X(-5)____3X(-5)
2<3 2X(-0.5)_____ 3X(-0.5)
你发现了什么?
<
<
>
>
>
做一做
同乘正数
同乘负数
P7-8
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
如果a>b,c<0 ,那么ac不等式的两边都乘以(或除以)同一个负数,不等号的方向改变;
如果a>b,c>0 ,那么ac>bc
不等式性质3
不等式性质2
口诀:负见乘除方向变
1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21 >- 28
-1<0
1、在不等式-8<0的两边都除以-8可得 。
2、在不等式-3 x<3的两边都除以-3可得 。
3、在不等式-3>-4的两边都乘以-3可得 。
4、在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
3
1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -5 >-1 (2) - 2 x > 3
(3) x >5 (4) -4 x < 3 - x
③④ 同学回答
解 (1)根据不等式的性质1,两边都加上5得:
x-5+5 > - 1+5
即 x > 4
(2)根据不等式的性质3,两边都除以-2 得:
即 x <-
① 不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
练习1,将下列不等式化成“x>a”或“x的形式:
(1)x-5>-1 (2)-2x>3
解:(1)根据不等式的基本性质1,
两边都加上5,得 x>-1+5
即 x>4
(2)根据不等式的基本性质3,
两边都除以-2,得 -2x÷(-2)<3÷(-2)
即 x<
练习2,若a-b<0,则下列各式中一定成立
的是( )
A.a>b B.ab>0
C. D.-a>-b
例3,若x是任意实数,则下列不等式中,
恒成立的是( )
A.3x>2x B.3x2>2x2
C.3+x>2 D.3+x2>2
D
D
练习3:(1)由xmy的条件是( )
A . m≥0 B . m≤0 C. m>0 D. m<0
(2)若mx1,则应为( )
A. m<0 B. m>0 C. m≤0 D. m≥0
(3)若m是有理数,则-7m与3m的大小关系应是( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定
D
A
D
比较2a与a的大小
(1)当a>0时,2a>a;
(2)当a=0时,2a=a;
(3)当a<0时,2a知识形成
不等式的基本性质
文字表示 符号表示
(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
(2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
若a(或a-c b-c)
若ac
a
b
c
<
<
<
若a0,
则ac bc(或 )
c
a
b
c
<
>
>
知识形成
不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
若a(2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
若a0, 则acc
a
<
b
c
若abc(或 )
c
a
>
b
c
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
等式的基本性质
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
若a=b,则a+c=b+c(或a-c=b-c)
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则ac=bc(或 , c≠0)
c
a
=
b
c
注意
1. 不等式、等式性质的异同点.
2. 对于
零.
3. 特别注意.
“<”(或“≤”),“>”(或“≥”)
1、不等式
2、理解关键词意义
非负数
不小于
不大于
非正数
至少(最少)
不超过
>
<
<
1、用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3
1、观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
同一个整式
等式的两边都加上(或减去) 或 ,所得的结果仍是等式。
等式的基本性质1:
2、继续观察下面这几个式子,完成下面的填空。
∵
∴
∴
同一个数
等式的两边都乘以(或除以) (除数不能为零),所得的结果仍是等式。
等式的基本性质2:
那么不等式有没有类似的性质呢?
不等式 两边都加上(或减去)同一个数 不等号方向是否改变了
7 > 4 7+5>4+5
-3<4 -3-7<4-7
… … …
不等式的性质1:
不等式的两边都加上(或减去)同一个整式,不等号的方向不变。
如果 ,那么
<
没有改变
没有改变
你发现了什么?
完成下列填空:
2<3 2X5 ____ 3X5
2<3 2X.05 ____3X0.5
2<3 2X(-1)____3X(-1)
2<3 2X(-5)____3X(-5)
2<3 2X(-0.5)_____ 3X(-0.5)
你发现了什么?
<
<
>
>
>
做一做
同乘正数
同乘负数
P7-8
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
如果a>b,c<0 ,那么ac
如果a>b,c>0 ,那么ac>bc
不等式性质3
不等式性质2
口诀:负见乘除方向变
1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。
减去5
2<17
-1>-8
-21 >- 28
-1<0
1、在不等式-8<0的两边都除以-8可得 。
2、在不等式-3 x<3的两边都除以-3可得 。
3、在不等式-3>-4的两边都乘以-3可得 。
4、在不等式 的两边都乘以-1可得 。
1>0
9<12
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
3
1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -5 >-1 (2) - 2 x > 3
(3) x >5 (4) -4 x < 3 - x
③④ 同学回答
解 (1)根据不等式的性质1,两边都加上5得:
x-5+5 > - 1+5
即 x > 4
(2)根据不等式的性质3,两边都除以-2 得:
即 x <-
① 不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
本节重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
练习1,将下列不等式化成“x>a”或“x
(1)x-5>-1 (2)-2x>3
解:(1)根据不等式的基本性质1,
两边都加上5,得 x>-1+5
即 x>4
(2)根据不等式的基本性质3,
两边都除以-2,得 -2x÷(-2)<3÷(-2)
即 x<
练习2,若a-b<0,则下列各式中一定成立
的是( )
A.a>b B.ab>0
C. D.-a>-b
例3,若x是任意实数,则下列不等式中,
恒成立的是( )
A.3x>2x B.3x2>2x2
C.3+x>2 D.3+x2>2
D
D
练习3:(1)由x
A . m≥0 B . m≤0 C. m>0 D. m<0
(2)若mx
A. m<0 B. m>0 C. m≤0 D. m≥0
(3)若m是有理数,则-7m与3m的大小关系应是( )
A. -7m<3m B. -7m>3m C. -7m≤3m D. 不能确定
D
A
D
比较2a与a的大小
(1)当a>0时,2a>a;
(2)当a=0时,2a=a;
(3)当a<0时,2a
不等式的基本性质
文字表示 符号表示
(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
(2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
若a
若ac
a
b
c
<
<
<
若a0,
则ac bc(或 )
c
a
b
c
<
>
>
知识形成
不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
若a
若a
a
<
b
c
若a
c
a
>
b
c
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
等式的基本性质
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
若a=b,则a+c=b+c(或a-c=b-c)
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则ac=bc(或 , c≠0)
c
a
=
b
c
注意
1. 不等式、等式性质的异同点.
2. 对于
零.
3. 特别注意.
