人教版数学七年级下册 第九章不等式与不等式组复习课 课件(共48张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第九章不等式与不等式组复习课 课件(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 16:58:19 | ||
图片预览



文档简介
(共48张PPT)
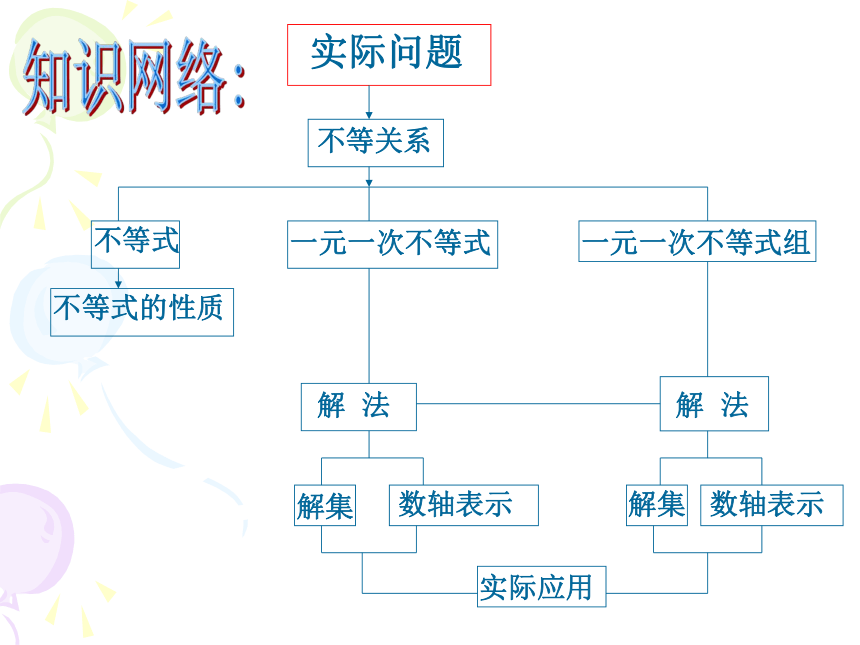
实际问题
不等关系
不等式
一元一次不等式
一元一次不等式组
不等式的性质
解集
解集
数轴表示
数轴表示
解 法
解 法
实际应用
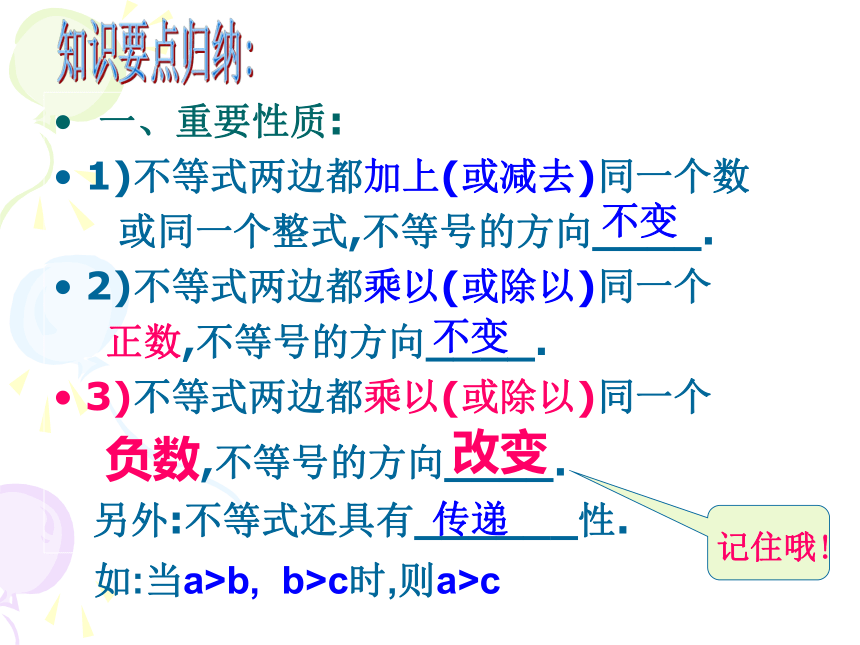
一、重要性质:
1)不等式两边都加上(或减去)同一个数
或同一个整式,不等号的方向____.
2)不等式两边都乘以(或除以)同一个
正数,不等号的方向____.
3)不等式两边都乘以(或除以)同一个
负数,不等号的方向____.
另外:不等式还具有______性.
如:当a>b, b>c时,则a>c
不变
不变
改变
记住哦!
传递
一、要点、考点聚焦
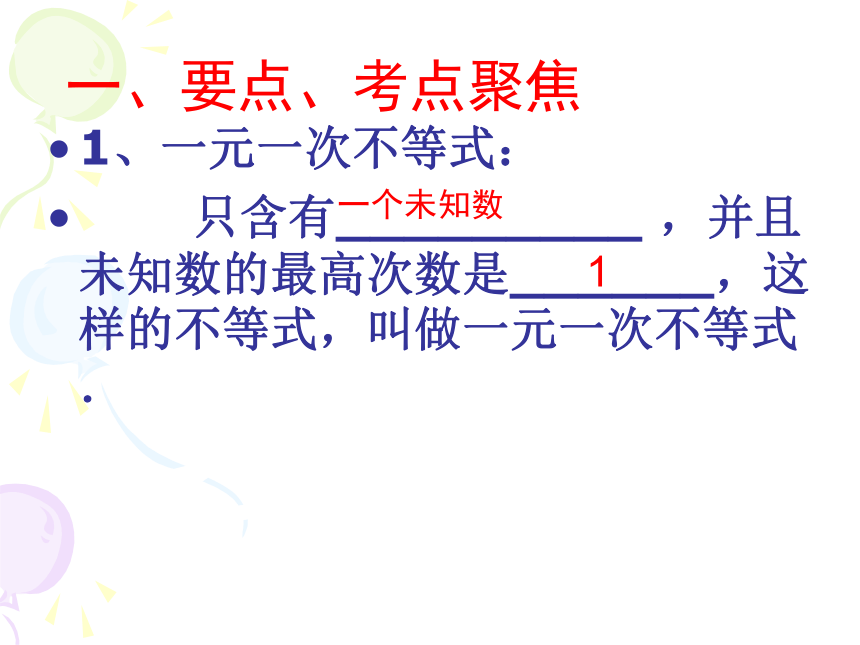
1、一元一次不等式:
只含有_________ ,并且未知数的最高次数是______,这样的不等式,叫做一元一次不等式.
一个未知数
1
解 去分母 去括号 移项 合并同类项
系数化为1等步骤.
一元一次不等式和解一元一次方程类似,有
区别在哪里
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
1、一元一次不等式的解法
二、方法与过程
2、一元一次不等式组的解法
(1)、先分别求出不等式组中各个不等式的解集。
(2)、利用数轴找出各个不等式的解集的公共部分。
(3)、写出不等式组的解集。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
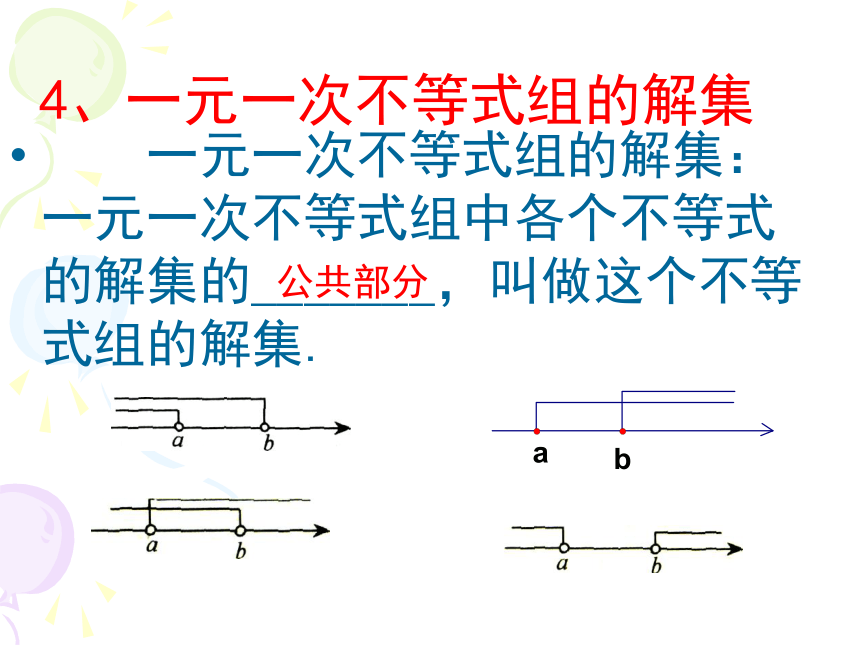
4、一元一次不等式组的解集
一元一次不等式组的解集:一元一次不等式组中各个不等式的解集的_______,叫做这个不等式组的解集.
公共部分
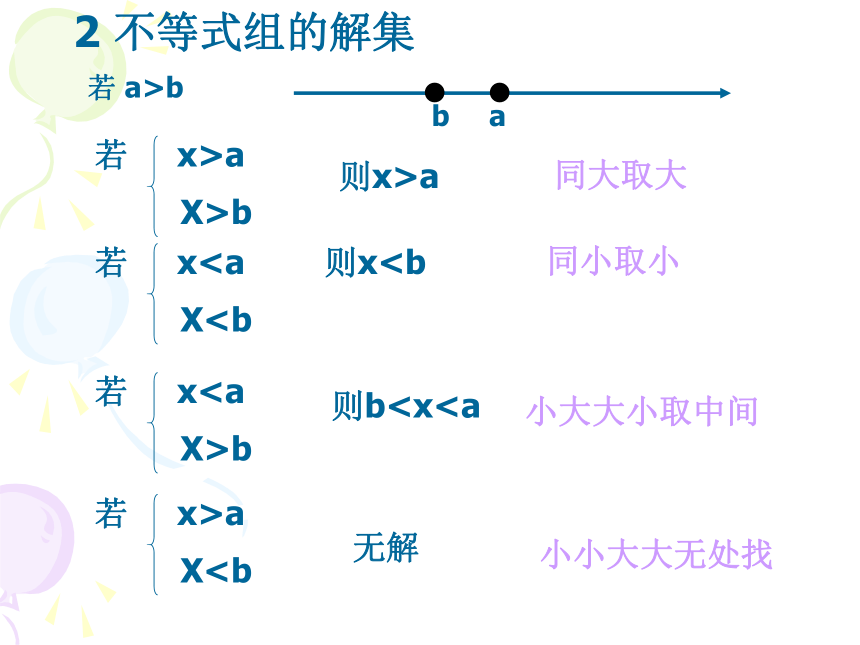
2 不等式组的解集
若 a>b
a
b
若 x>a
X>b
则x>a
同大取大
若 xX则x同小取小
若 x>a
X无解
小小大大无处找
若 xX>b
则b小大大小取中间
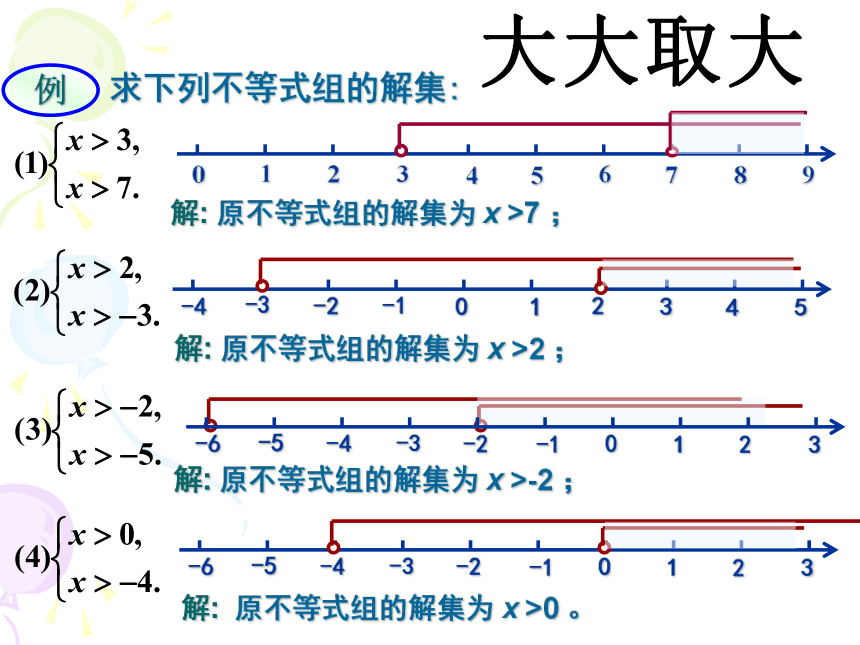
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
-6
1
0
-1
-2
-4
-5
-3
2
3
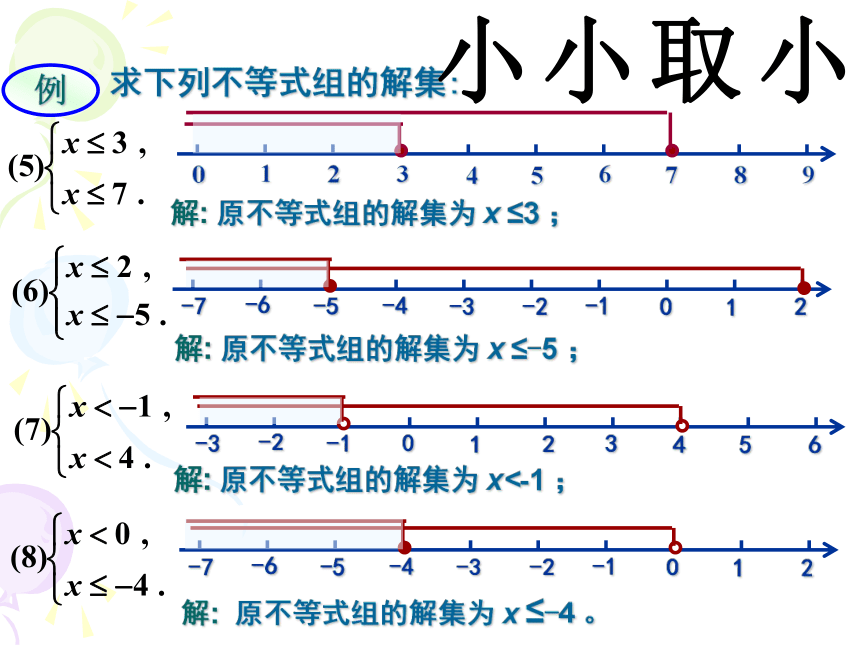
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
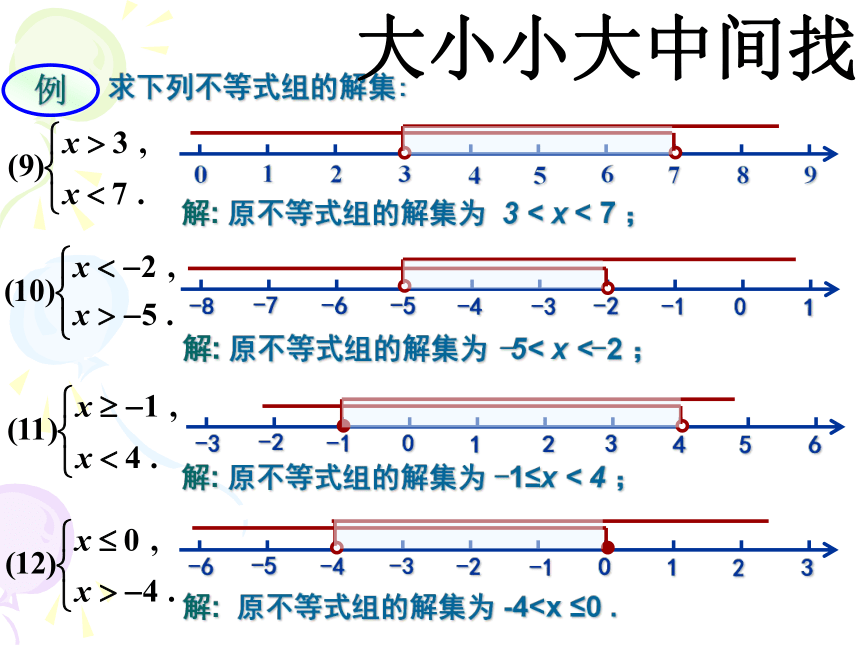
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4大小小大中间找
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大小小解不了
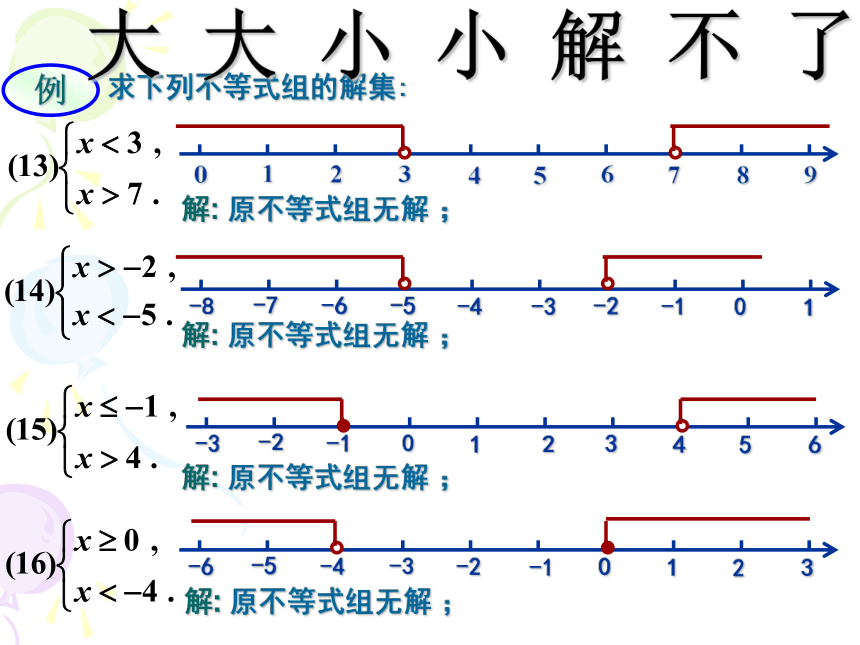
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大小小解不了
知识应用
2x-1>x-2
x+8>4x-1
例2.
解下列不等式组
①
②
解:解不等式①,得 x> -1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 -1随堂练习
2x>1
x-3<0
{
(1)
x-2>-1
3x+1<8
{
(2)
1. 解下列不等式组
2x-1>x+1
x+8 4x-1
{
(3)
2x+3<5
3x-2 <4
{
(4)
大大取较大
x>3.5
小小取较小
x<-1
-13、用一元一次不等式(组)解决实际问题的步骤:
实际问题
设一个未知数
列不等式(组)
解不等式(组)
检验解是否符合情况
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
与解一元一次方程方法类似
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
我来试试:
2.解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
与解方程组的方法完全不同
3、求不等式(组)的特殊解:
(1)求不等式 3x+1≥4x-5的正整数解.
(2)求不等式组 的整数解.
(1)求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
②
①
解:解不等式①得:x<5
解不等式②得:x≥1.4
∴原不等式组的解集为1.4≤x<5
∵满足1.4≤x<5的正整数解为:2、3、4
∴原不等式组的正整数解:2、3、4
(2)求不等式组 的整数解.
解:
0
4
由不等式①得: x>2
由不等式②得: x≤4
∴ 不等式组的解集为:2<x≤4
1
2
-1
3
5
6
7
8
不等式组的整数解为:3、4
例3 m取何值时,关于x的方程
解:
根据题意,得
解得 m>2
的解大于1。
2、关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )
A、0 B、-3
C、-2 D、-1
B
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
学校要到体育用品商场购买篮球和排球共100只.已知篮球、排球的单价分别为130元、100元。购买100只球所花费用多于11800元,但不超过11900元。你认为有哪些购买方案?
某校今年冬季烧煤取暖时间为4个月。如果每月比计划多烧5吨煤, 那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,呢么取暖用煤总量不足68吨.
解: 设计划每月烧煤的数量为x吨.
该校计划每月烧煤多少吨
4(x+5)>100, ①
4(x-5)<68. ②
”一元一次不等式组” 的定义
依题意,
.
1. 根据下图所示,对a、b、c三种物体的重量判断正确的是 ( )
A. ac D. b2.点A( , )在第三象限,则m的取值范围是( )
A. B. C. D.
C
C
3. 八(1)班学生到阅览室读书,班长问老师要分成几个小组,老师风趣地说:
假如我把43本书分给各个小组,若每组8本,还有剩余;若每组9本,却又不够.你知道该分几个小组吗
请你帮助班长分组!
2、已知不等式组 有解,则a的取值范围为___
(A)a>-2 (B)a≥-2
(C)a<2 (D)a≥2 .
1.关于x的不等式
的解集如图
所示,则a 的取值是( )
A.0 B.—3 C.—2 D.—1
3.根据下列条件,分别求出a的值或取值范围:
1)已知不等式 的解集是x<5,求a的值
2)已知x=5是不等式 的解.求a的取值范围。
练习一
1、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
C
2、如果不等式组
的解集是x>a,则a_______b。
C
0 m 1 3/2 2
例1.若不等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
a>3
(较大)
(较小)
(较大)
(较小)
m+1≤ 2m - 1
m≥2
随堂练习三
②
①
解:由方程组得
∵x+y<0
解之得
解不等式组:
变式1:两个代数式x-1与x+3的值的符号相同,则x的取值范围是多少?
变式2:若 ,不等式
组 的解集是多少?
变式3:方程组 的解是
则不等式组 的解是多少?
在方程组 中,已知x>0,y<0
求m的取值范围.
一变:
在方程组 中,已知xy<0
求m的取值范围.
三变:
二变:
在方程组 中,已知xy<0
且x,y都是整数,求m的值.
已知在方程组 中,xy<0
化简: .
2≤3x-7<8
①
②
解:解不等式①,得x≥3
解不等式② ,得
∴不等式组的解集为:3≤x<5
2≤-3x-7<8
解:2+7≤-3x<8+7
9≤-3x<15
-3≥x>-5
-5解:去分母-9≤2x-1<15
移项 -8≤2x<16
系数化为1 -4≤x<8
(较大)
(较小)
(较大)
(较小)
2.k取何值时,方程组
中的x大于1,y小于1。
实际问题
不等关系
不等式
一元一次不等式
一元一次不等式组
不等式的性质
解集
解集
数轴表示
数轴表示
解 法
解 法
实际应用
一、重要性质:
1)不等式两边都加上(或减去)同一个数
或同一个整式,不等号的方向____.
2)不等式两边都乘以(或除以)同一个
正数,不等号的方向____.
3)不等式两边都乘以(或除以)同一个
负数,不等号的方向____.
另外:不等式还具有______性.
如:当a>b, b>c时,则a>c
不变
不变
改变
记住哦!
传递
一、要点、考点聚焦
1、一元一次不等式:
只含有_________ ,并且未知数的最高次数是______,这样的不等式,叫做一元一次不等式.
一个未知数
1
解 去分母 去括号 移项 合并同类项
系数化为1等步骤.
一元一次不等式和解一元一次方程类似,有
区别在哪里
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
1、一元一次不等式的解法
二、方法与过程
2、一元一次不等式组的解法
(1)、先分别求出不等式组中各个不等式的解集。
(2)、利用数轴找出各个不等式的解集的公共部分。
(3)、写出不等式组的解集。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
4、一元一次不等式组的解集
一元一次不等式组的解集:一元一次不等式组中各个不等式的解集的_______,叫做这个不等式组的解集.
公共部分
2 不等式组的解集
若 a>b
a
b
若 x>a
X>b
则x>a
同大取大
若 x
若 x>a
X
小小大大无处找
若 x
则b
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
-6
1
0
-1
-2
-4
-5
-3
2
3
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大小小解不了
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大小小解不了
知识应用
2x-1>x-2
x+8>4x-1
例2.
解下列不等式组
①
②
解:解不等式①,得 x> -1.
解不等式② ,得 x<3.
在数轴上表示不等式①, ②的解集
-1
3
所以这个不等式组的解集是 -1
2x>1
x-3<0
{
(1)
x-2>-1
3x+1<8
{
(2)
1. 解下列不等式组
2x-1>x+1
x+8 4x-1
{
(3)
2x+3<5
3x-2 <4
{
(4)
大大取较大
x>3.5
小小取较小
x<-1
-1
实际问题
设一个未知数
列不等式(组)
解不等式(组)
检验解是否符合情况
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
与解一元一次方程方法类似
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
我来试试:
2.解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
与解方程组的方法完全不同
3、求不等式(组)的特殊解:
(1)求不等式 3x+1≥4x-5的正整数解.
(2)求不等式组 的整数解.
(1)求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
②
①
解:解不等式①得:x<5
解不等式②得:x≥1.4
∴原不等式组的解集为1.4≤x<5
∵满足1.4≤x<5的正整数解为:2、3、4
∴原不等式组的正整数解:2、3、4
(2)求不等式组 的整数解.
解:
0
4
由不等式①得: x>2
由不等式②得: x≤4
∴ 不等式组的解集为:2<x≤4
1
2
-1
3
5
6
7
8
不等式组的整数解为:3、4
例3 m取何值时,关于x的方程
解:
根据题意,得
解得 m>2
的解大于1。
2、关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )
A、0 B、-3
C、-2 D、-1
B
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
学校要到体育用品商场购买篮球和排球共100只.已知篮球、排球的单价分别为130元、100元。购买100只球所花费用多于11800元,但不超过11900元。你认为有哪些购买方案?
某校今年冬季烧煤取暖时间为4个月。如果每月比计划多烧5吨煤, 那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,呢么取暖用煤总量不足68吨.
解: 设计划每月烧煤的数量为x吨.
该校计划每月烧煤多少吨
4(x+5)>100, ①
4(x-5)<68. ②
”一元一次不等式组” 的定义
依题意,
.
1. 根据下图所示,对a、b、c三种物体的重量判断正确的是 ( )
A. a
A. B. C. D.
C
C
3. 八(1)班学生到阅览室读书,班长问老师要分成几个小组,老师风趣地说:
假如我把43本书分给各个小组,若每组8本,还有剩余;若每组9本,却又不够.你知道该分几个小组吗
请你帮助班长分组!
2、已知不等式组 有解,则a的取值范围为___
(A)a>-2 (B)a≥-2
(C)a<2 (D)a≥2 .
1.关于x的不等式
的解集如图
所示,则a 的取值是( )
A.0 B.—3 C.—2 D.—1
3.根据下列条件,分别求出a的值或取值范围:
1)已知不等式 的解集是x<5,求a的值
2)已知x=5是不等式 的解.求a的取值范围。
练习一
1、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
C
2、如果不等式组
的解集是x>a,则a_______b。
C
0 m 1 3/2 2
例1.若不等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
a>3
(较大)
(较小)
(较大)
(较小)
m+1≤ 2m - 1
m≥2
随堂练习三
②
①
解:由方程组得
∵x+y<0
解之得
解不等式组:
变式1:两个代数式x-1与x+3的值的符号相同,则x的取值范围是多少?
变式2:若 ,不等式
组 的解集是多少?
变式3:方程组 的解是
则不等式组 的解是多少?
在方程组 中,已知x>0,y<0
求m的取值范围.
一变:
在方程组 中,已知xy<0
求m的取值范围.
三变:
二变:
在方程组 中,已知xy<0
且x,y都是整数,求m的值.
已知在方程组 中,xy<0
化简: .
2≤3x-7<8
①
②
解:解不等式①,得x≥3
解不等式② ,得
∴不等式组的解集为:3≤x<5
2≤-3x-7<8
解:2+7≤-3x<8+7
9≤-3x<15
-3≥x>-5
-5
移项 -8≤2x<16
系数化为1 -4≤x<8
(较大)
(较小)
(较大)
(较小)
2.k取何值时,方程组
中的x大于1,y小于1。
