中心对称
图片预览





文档简介
课件32张PPT。23.2.2 中心对称图形第23章 旋转土台九年制学校 蔡帮均教学目标:
知识与技能:了解中心对称图形的概念及中心对称图形
的对称中心的概念,掌握这两个概念的应用.
过程与方法:复习两个图形关于中心对称的有关概念,
利用这个所学知识探索一个图形是中心对称
图形的有关概念及其它的运用.
情感态度与价值观: 让学生经历观察、操作等过程,了
解旋转180°的特殊旋转──中心对称图形
的概念,获得知识,体验成功,享受学习乐趣。
教学重难点:
重点:中心对称图形的有关概念及其它们的运用.
难点:区别关于中心对称的两个图形和中心对称图形.
教学方法:自主探究法
一.知识回顾
1.中心对称的定义:把一个图形绕着某一点旋转1800,如果它能与另一个图形重合,就说这两个图形关于这个点成中心对称. 2. 中心对称的性质:
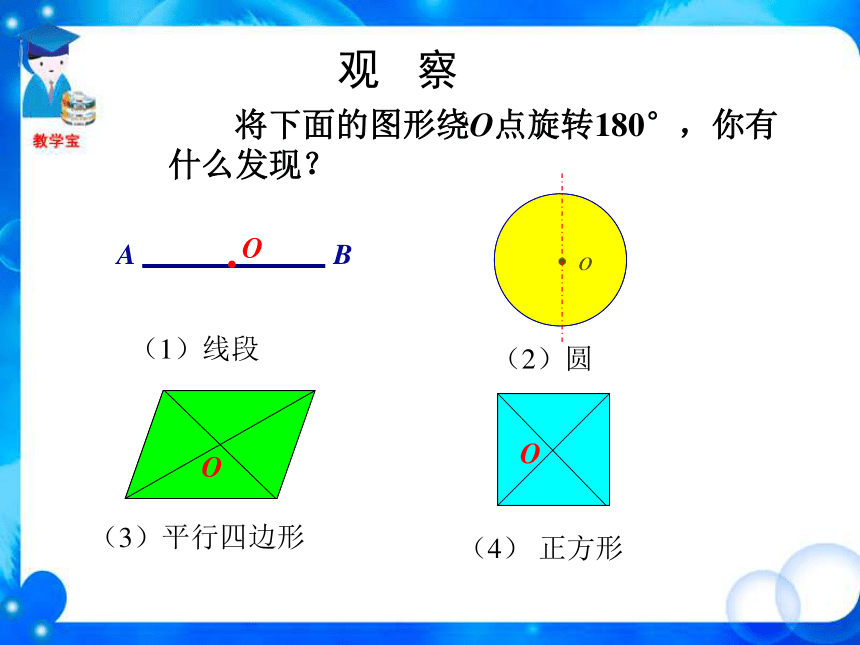
⑴关于中心对称的两个图形是全等图形⑵关于中心对称的两个图形,对称点连线都经过对称中心且被对称中心平分(3)关于中心对称的两个图形,对称线段平行且相等(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?O(1)这些图形有什么共同的特征?都是旋转对称图形。(2)这些图形的不同点在哪?分别绕旋转中心旋转
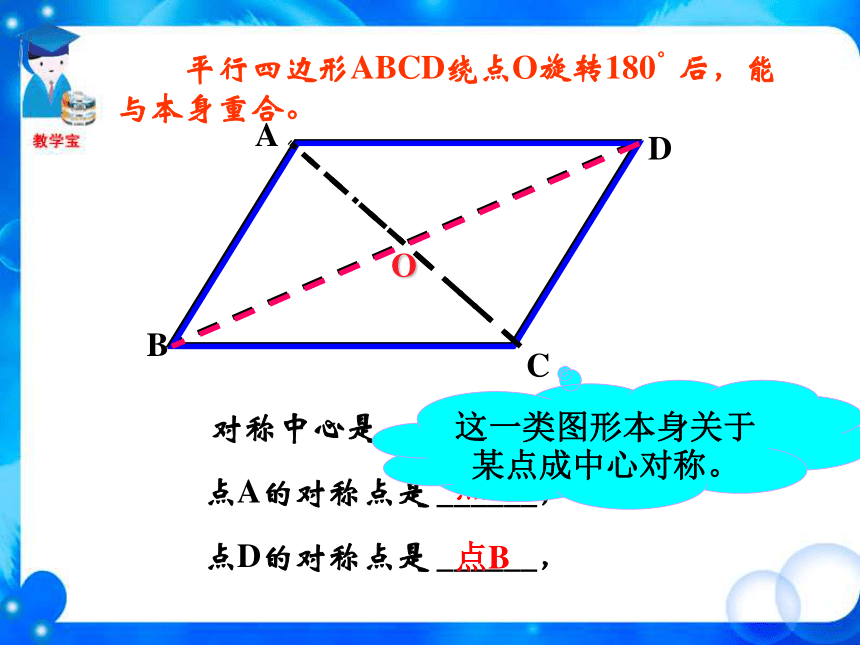
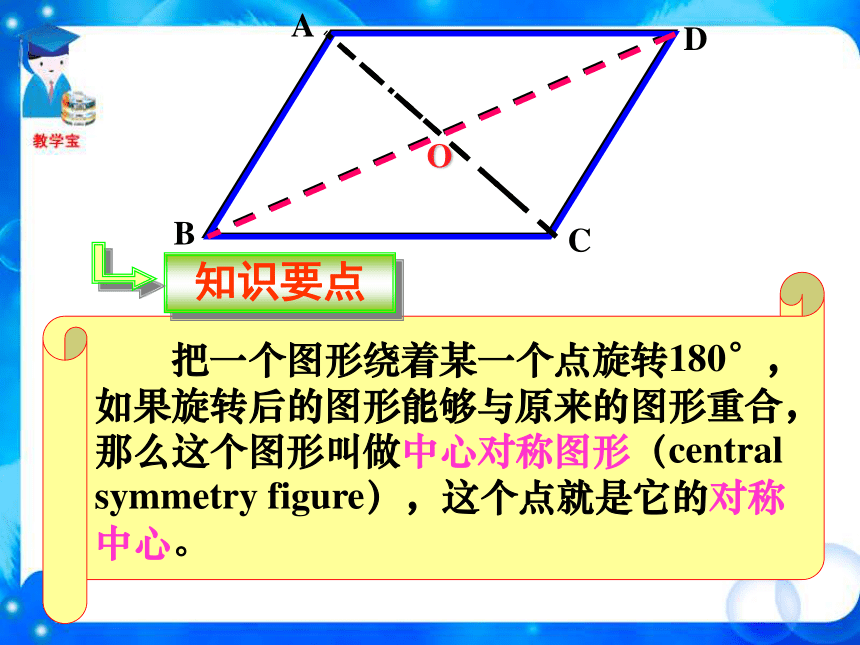
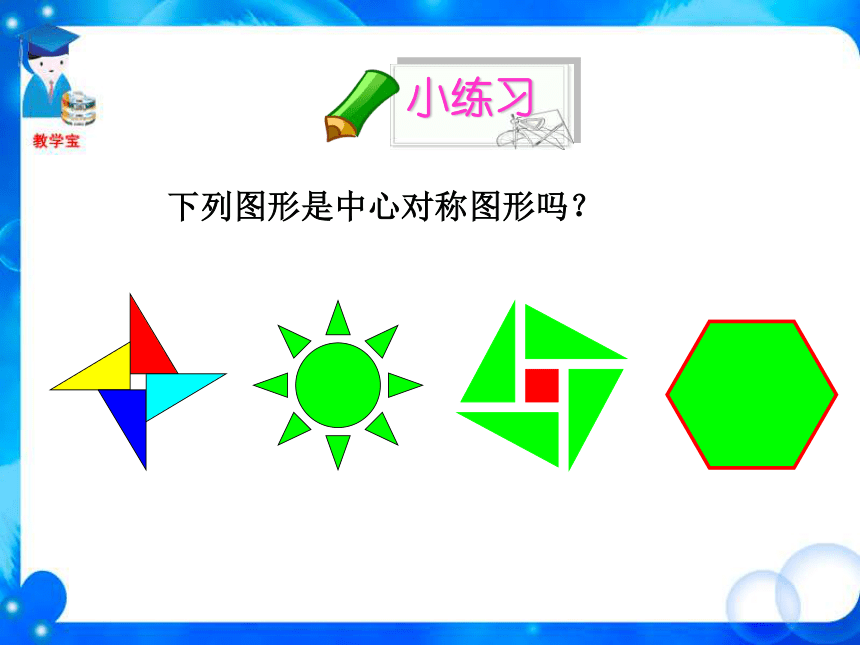
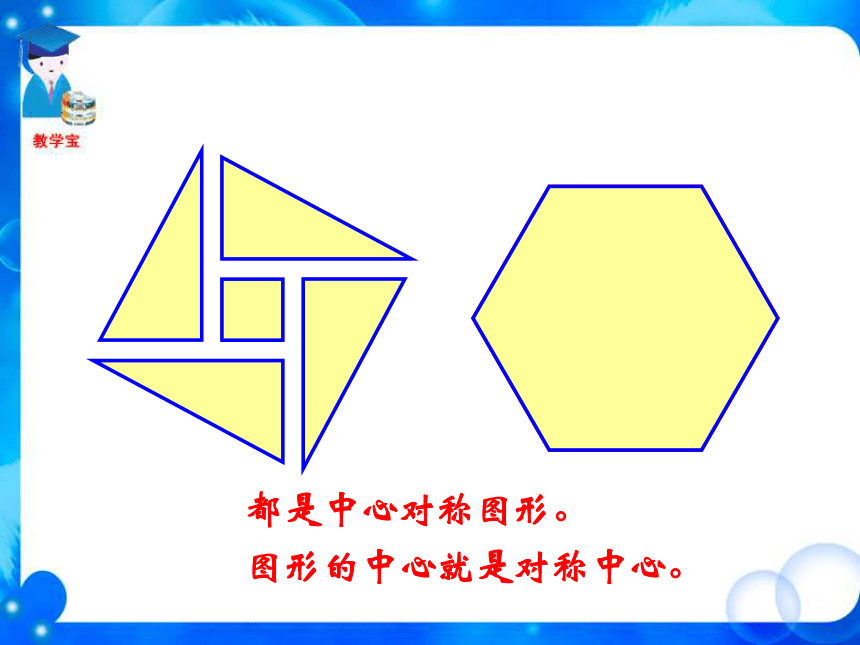
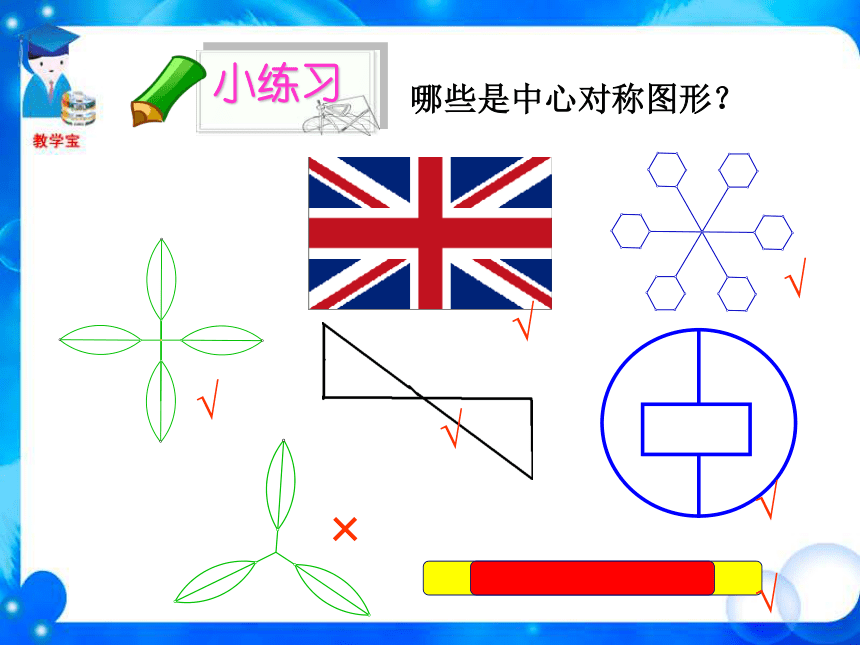
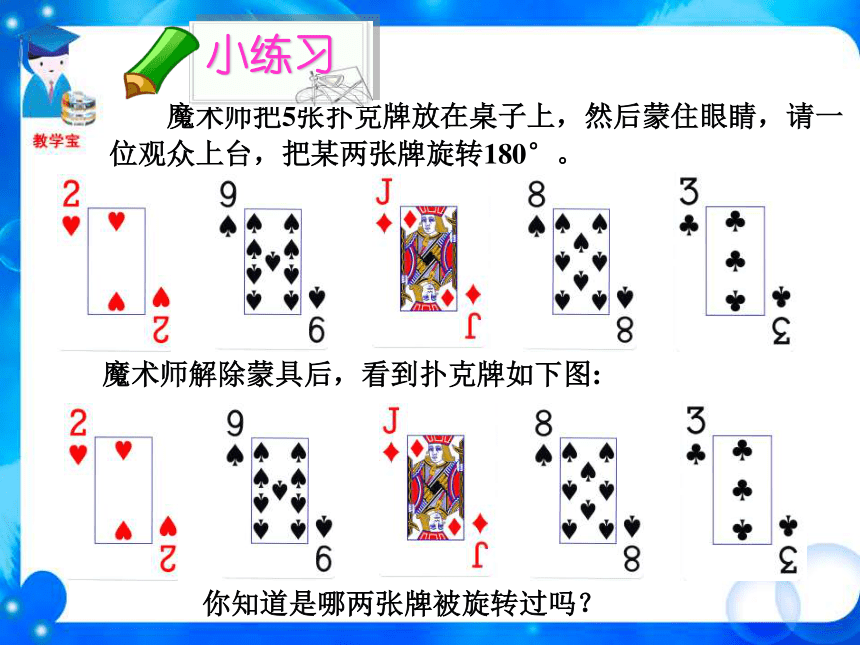
了多少度? 第一个图形的旋转角度为120°或240 °,第二个图形的旋转角度为72°或144°或216°或288°。后三个图形的旋转角度都为180°,第二,三个是轴对称图形。后三个图形都是旋转1800后能与自身重合复习与思考OBACD对称中心是 ______,点O点A的对称点是 ______,点D的对称点是 ______,点C点B 平行四边形ABCD绕点O旋转180°后,能与本身重合。这一类图形本身关于某点成中心对称。 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形(central symmetry figure),这个点就是它的对称中心。 OBACD下列图形是中心对称图形吗?小练习认真观察旋转180°后……都是中心对称图形。图形的中心就是对称中心。都是中心对称图形。图形的中心就是对称中心。哪些是中心对称图形?小练习√×√√√√√ 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°。 魔术师解除蒙具后,看到扑克牌如下图:你知道是哪两张牌被旋转过吗?小练习汉代铜镜——中心对称图形中心对称图形中心对称图形旋转前后的图形完全重合轴对称图形中心对称图形图形绕对称中心旋转 180°翻转前后的图形完全重合中心对称图形与轴对称图形的区别与联系 课堂小结轴对称图形与中心对称图形的比较中心对称与中心对称图形的区别与联系把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分________①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 随堂练习 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√√ ×√ ×√√ ×√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5)5.若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
6.如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB运用 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√ 8. 在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z小结与归纳这一节课你学会了什么,请谈谈你的收获你存在的困惑是?作业布置:课堂作业:
P68 习题23.2 3、4
课后作业:
《练习册》第26---27
的对称中心的概念,掌握这两个概念的应用.
过程与方法:复习两个图形关于中心对称的有关概念,
利用这个所学知识探索一个图形是中心对称
图形的有关概念及其它的运用.
情感态度与价值观: 让学生经历观察、操作等过程,了
解旋转180°的特殊旋转──中心对称图形
的概念,获得知识,体验成功,享受学习乐趣。
教学重难点:
重点:中心对称图形的有关概念及其它们的运用.
难点:区别关于中心对称的两个图形和中心对称图形.
教学方法:自主探究法
一.知识回顾
1.中心对称的定义:把一个图形绕着某一点旋转1800,如果它能与另一个图形重合,就说这两个图形关于这个点成中心对称. 2. 中心对称的性质:
⑴关于中心对称的两个图形是全等图形⑵关于中心对称的两个图形,对称点连线都经过对称中心且被对称中心平分(3)关于中心对称的两个图形,对称线段平行且相等(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?O(1)这些图形有什么共同的特征?都是旋转对称图形。(2)这些图形的不同点在哪?分别绕旋转中心旋转
了多少度? 第一个图形的旋转角度为120°或240 °,第二个图形的旋转角度为72°或144°或216°或288°。后三个图形的旋转角度都为180°,第二,三个是轴对称图形。后三个图形都是旋转1800后能与自身重合复习与思考OBACD对称中心是 ______,点O点A的对称点是 ______,点D的对称点是 ______,点C点B 平行四边形ABCD绕点O旋转180°后,能与本身重合。这一类图形本身关于某点成中心对称。 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形(central symmetry figure),这个点就是它的对称中心。 OBACD下列图形是中心对称图形吗?小练习认真观察旋转180°后……都是中心对称图形。图形的中心就是对称中心。都是中心对称图形。图形的中心就是对称中心。哪些是中心对称图形?小练习√×√√√√√ 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°。 魔术师解除蒙具后,看到扑克牌如下图:你知道是哪两张牌被旋转过吗?小练习汉代铜镜——中心对称图形中心对称图形中心对称图形旋转前后的图形完全重合轴对称图形中心对称图形图形绕对称中心旋转 180°翻转前后的图形完全重合中心对称图形与轴对称图形的区别与联系 课堂小结轴对称图形与中心对称图形的比较中心对称与中心对称图形的区别与联系把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分________①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 随堂练习 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√√ ×√ ×√√ ×√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5)5.若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
6.如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB运用 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√ 8. 在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z小结与归纳这一节课你学会了什么,请谈谈你的收获你存在的困惑是?作业布置:课堂作业:
P68 习题23.2 3、4
课后作业:
《练习册》第26---27
同课章节目录
