2021-2022学年北师大版九年级上数学第六章反比例函数综合复习题(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级上数学第六章反比例函数综合复习题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 20:19:35 | ||
图片预览

文档简介
2021-2022北师大版九上数学反比例函数综合复习题
一、单选题
1.(2020九上·灌阳期中)下列各点中,在反比例函数 图象上的是( )
A. (-1,8) B. (-2,4) C. (1,7) D. (2,4)
2.下列选项,是反比例函数关系的为( )
A. 在直角三角形中,30°角所对的直角边 与斜边 之间的关系
B. 在等腰三角形中,顶角 与底角 之间的关系
C. 圆的面积 与它的直径 之间的关系
D. 面积为20的菱形,其中一条对角线 与另一条对角线 之间的关系
3.(2019九上·陵县月考)已知函数y=(m+2)x 是反比例函数,则m的值是( )
A. 2 B. C. D.
4.(2019九上·双台子月考)如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为( )
A. 4 B. ﹣4 C. 8 D. ﹣8
5.(2020九上·历下期中)已知点A(﹣1,y1)、B(﹣2,y2)、C(3,y3)都在反比例函数y= 的图象上,则y1、y2、y3的关系是( )
A. y2>y1>y3 B. y2>y3>y1 C. y3>y1>y2 D. y3>y2>y1
6.(2020·南岸模拟)如图所示,直线y1=﹣ x与双曲线y= 交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
A. ﹣10 B. ﹣9 C. 6 D. 4
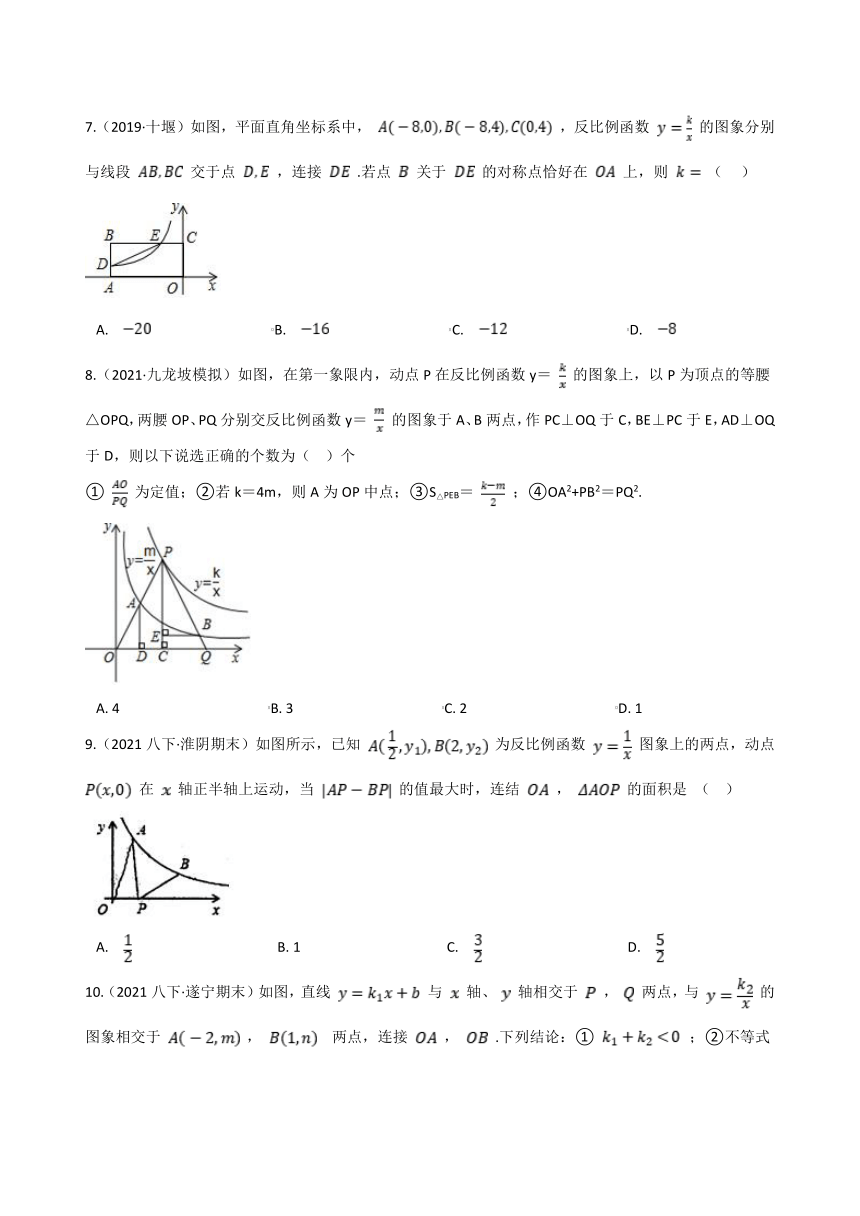
7.(2019·十堰)如图,平面直角坐标系中, ,反比例函数 的图象分别与线段 交于点 ,连接 .若点 关于 的对称点恰好在 上,则 ( )
A. B. C. D.
8.(2021·九龙坡模拟)如图,在第一象限内,动点P在反比例函数y= 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y= 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
① 为定值;②若k=4m,则A为OP中点;③S△PEB= ;④OA2+PB2=PQ2.
A. 4 B. 3 C. 2 D. 1
9.(2021八下·淮阴期末)如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( )
A. B. 1 C. D.
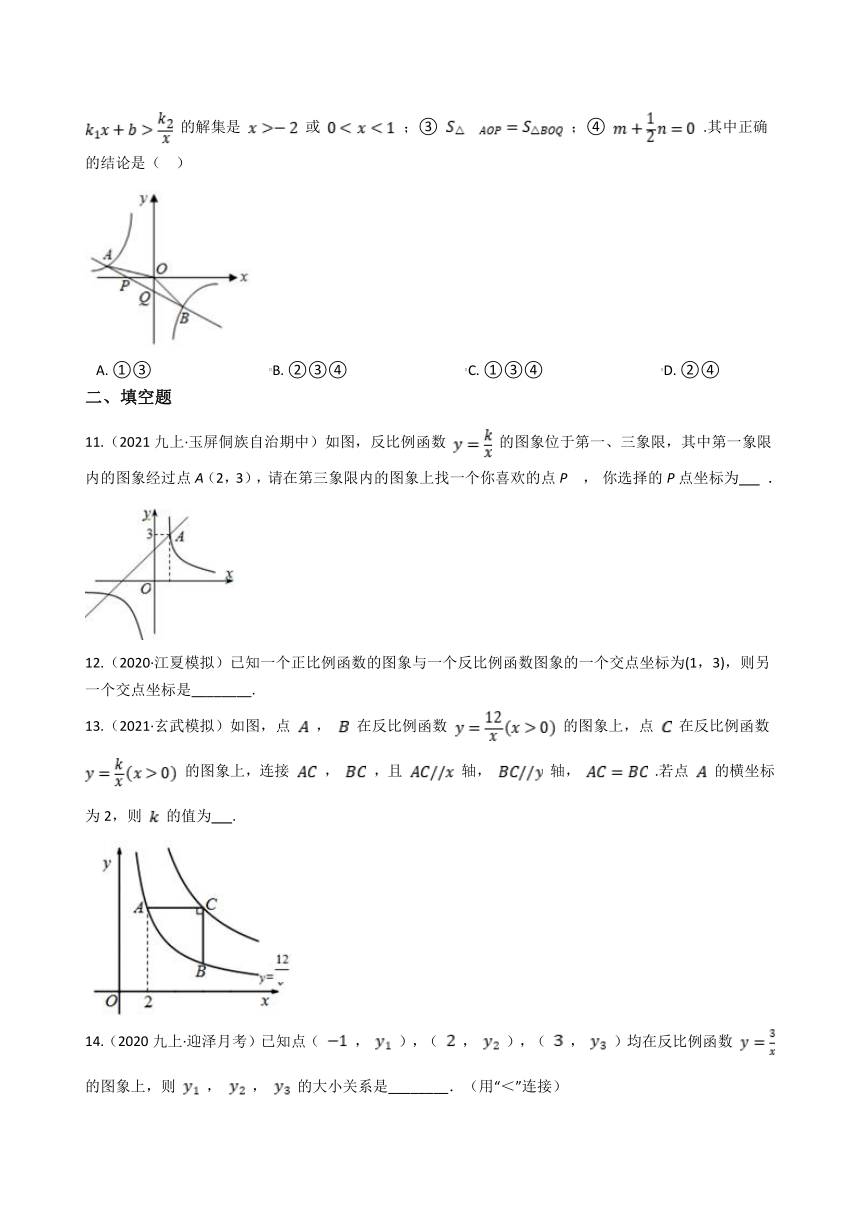
10.(2021八下·遂宁期末)如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A. ①③ B. ②③④ C. ①③④ D. ②④
二、填空题
11.(2021九上·玉屏侗族自治期中)如图,反比例函数 的图象位于第一、三象限,其中第一象限内的图象经过点A(2,3),请在第三象限内的图象上找一个你喜欢的点P , 你选择的P点坐标为 .
12.(2020·江夏模拟)已知一个正比例函数的图象与一个反比例函数图象的一个交点坐标为(1,3),则另一个交点坐标是________.
13.(2021·玄武模拟)如图,点 , 在反比例函数 的图象上,点 在反比例函数 的图象上,连接 , ,且 轴, 轴, .若点 的横坐标为2,则 的值为 .
14.(2020九上·迎泽月考)已知点( , ),( , ),( , )均在反比例函数 的图象上,则 , , 的大小关系是________.(用“<”连接)
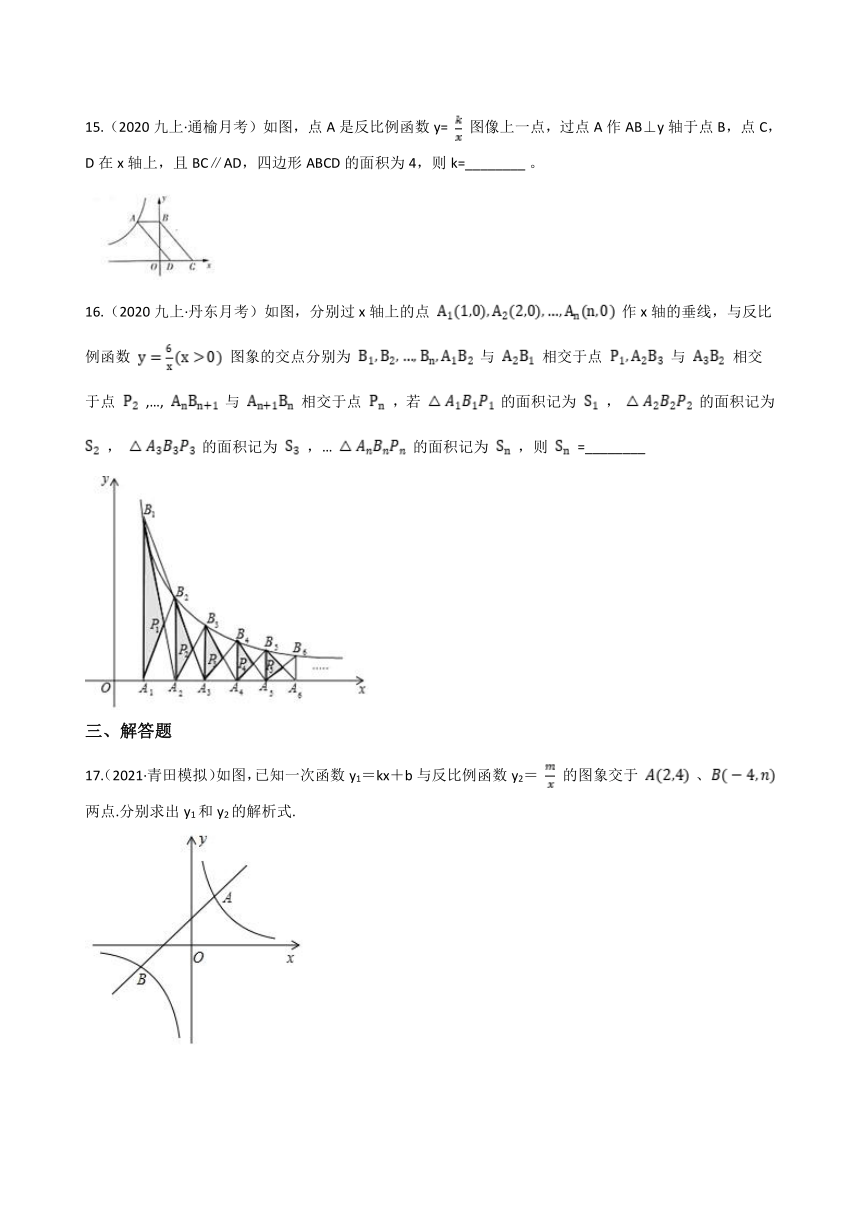
15.(2020九上·通榆月考)如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k=________ 。
16.(2020九上·丹东月考)如图,分别过x轴上的点 作x轴的垂线,与反比例函数 图象的交点分别为 与 相交于点 与 相交于点 ,…, 与 相交于点 ,若 的面积记为 , 的面积记为 , 的面积记为 ,… 的面积记为 ,则 =________
三、解答题
17.(2021·青田模拟)如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
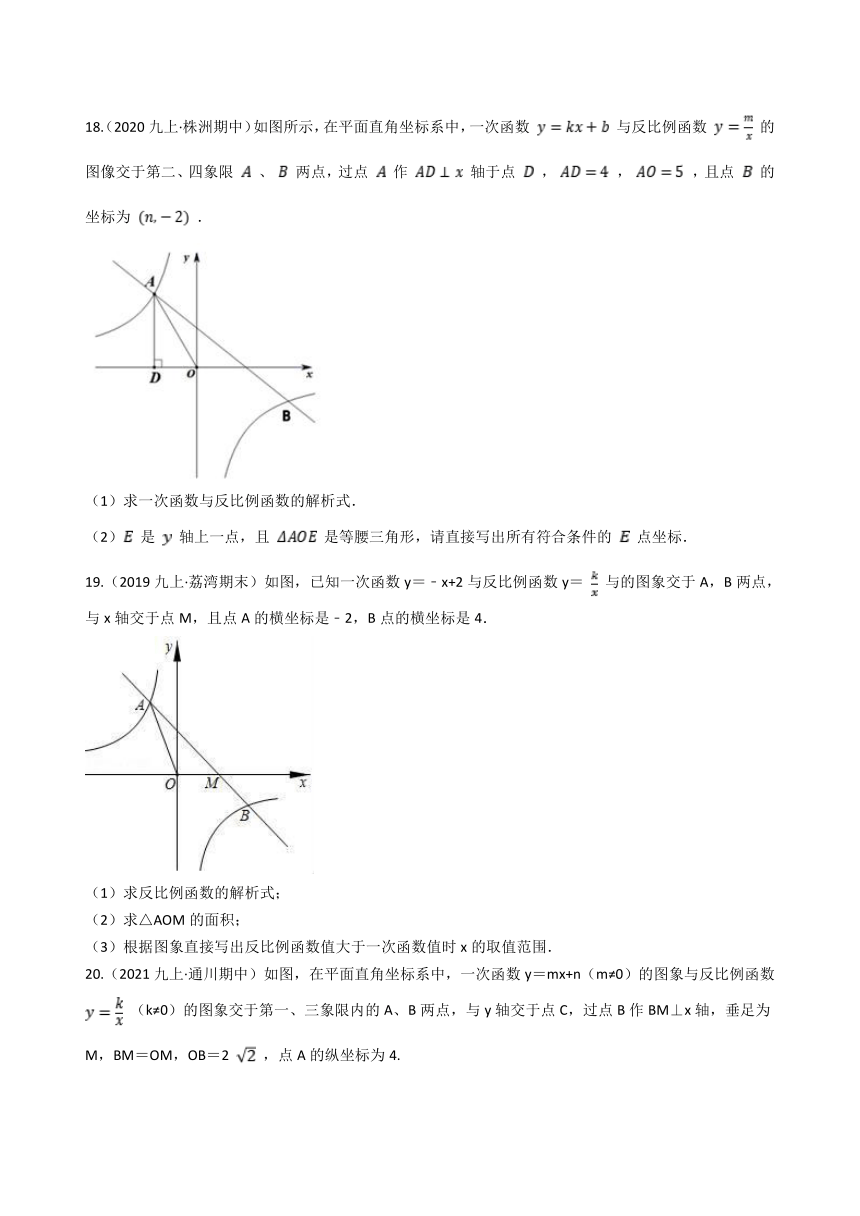
18.(2020九上·株洲期中)如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图像交于第二、四象限 、 两点,过点 作 轴于点 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式.
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
19.(2019九上·荔湾期末)如图,已知一次函数y=﹣x+2与反比例函数y= 与的图象交于A,B两点,与x轴交于点M,且点A的横坐标是﹣2,B点的横坐标是4.
(1)求反比例函数的解析式;
(2)求△AOM的面积;
(3)根据图象直接写出反比例函数值大于一次函数值时x的取值范围.
20.(2021九上·通川期中)如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数 (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2 ,点A的纵坐标为4.
(1)求一次函数的解析式;
(2)求不等式mx+n> 的解集;
(3)连接MC,AO在x轴上,是否存在点P使S△PAO= SMBOC , 若存在,求出P点坐标,若不存在,请说明理由.
21.(2021·深圳模拟)如图1,直线y1=kx+3与双曲线y2= (x>0)交于点P , PA⊥x轴于点A , PB⊥y轴于点B , 直线y1=kx+3分别交x轴、y轴于点C和点D , 且S△DBP=27, .
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM , 当△BCM为等腰三角形时,请直接写出点M的坐标.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:A、∵-1×8=-8≠8,∴该点不在函数图象上,故本选项错误;
B、∵-2×4=-8≠8,∴该点不在函数图象上,故本选项错误;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项错误;
D、2×4=8,∴该点在函数图象上,故本选项正确.
故答案为:D.
【分析】由于反比例函数y= 中,k=xy,即将各选项横、纵坐标分别相乘,其积为8者即为正确答案.
2.【答案】 D
【解析】【解答】解:A、由题意可知:y= , 是正比例函数关系,此选项不符合题意;
B、由题意可知 :y=180°-2x,是一次函数关系,此选项不符合题意;
C、由题意可知 :S=,是二次函数关系,此选项不符合题意;
D、由题意可知:是反比例函数关系,此选项符合题意;
故答案为 :D。
【分析】A、根据含30°直角三角形的斜边等于 30°角所对的直角边 的2倍,列出函数关系,根据函数特点即可判断出该函数是正比例函数关系,此选项不符合题意;
B、根据等腰三角形的两底角相等,及三角形的内角和定理即可建立出函数关系,根据函数特点即可判断出该函数是一次函数关系,此选项不符合题意;
C、根据圆的面积等于r2即可列出函数关系式,根据函数特点即可判断出该函数是二次函数关系,此选项不符合题意;
D、根据菱形的面积等于两对角线乘积的一半,即可列出函数关系式,根据函数特点即可判断出该函数是反比例函数关系,此选项符合题意。
3.【答案】 A
【解析】【解答】解:依题意得:m2-5=-1,且m+2≠0,
解得m=2.
故答案为:A .
【分析】根据反比例函数的定义得到m2-5=-1,且m+2≠0,由此求得m的值.
4.【答案】 D
【解析】【解答】解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴ ,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y= 的图象上,则mn=2,
∵点B在反比例函数y= 的图象上,
∴B点的坐标是( 2n,2m),
∴k= 2n 2m= 4mn= 8.
故答案为:D.
【分析】求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,根据条件得到△ACO∽△ODB,得到 ,然后用待定系数法即可.
5.【答案】 D
【解析】【解答】解:∵在反比例函数y= 中,k=1>0,
∴此函数图象在一、三象限,
∵﹣2<﹣1<0,
∴点A(﹣1,y1),B(﹣2,y2)在第三象限,
∴y1<y2<0,
∵3>0,
∴C(3,y3)点在第一象限,
∴y3>0,
∴y1 , y2 , y3的大小关系为y3>y2>y1 .
故答案为:D.
【分析】先根据函数解析式中的比例系数K,确定函数图像所在的象限,在根据各象限内点的坐标,特征及函数的增减性解答即可。
6.【答案】 B
【解析】【解答】解:∵直线y1=﹣ x与双曲线y= 交于A,B两点,
∴点A与点B关于原点对称,OA=OB,
∵AC⊥BC,
∴∠ACB=90°,
∴OA=OB=OC,
设A(t,﹣ t),则B(﹣t, t),
∴OA= =﹣ t,
∴OC=﹣ t,
∵S△ABC=15,
∴ ×(﹣ t)(﹣ t﹣ )=15,解得t=﹣ ,
∴A(﹣ ,2 ),
把A(﹣ ,2 )代入y= 得k=﹣ ×2 =﹣9.
故答案为:B.
【分析】先根据正比例函数和反比例函数的性质得到点 与点 关于原点对称, ,再根据直角三角形斜边上的中线性质得到 ,设 ,则 ,利用勾股定理表示出 ,则 ,接着利用三角形面积公式得到 ,解出 得到 , ,然后把 , 代入 中可求出 的值.
7.【答案】 C
【解析】【解答】解:过点 作 ,垂足为 ,设点 关于 的对称点为 ,连接 ,如图所示:
则 ,
易证
,
,
,
在反比例函数 的图象上,
,
在 中,由勾股定理:
即:
解得: 。
故答案为:C。
【分析】过点 作 ,垂足为 ,设点 关于 的对称点为 ,连接 ,如图所示:根据A,B,C三点的坐标特点得出 , 根据点的坐标与图形的性质分别用含k的式子表示出点D,E的坐标,根据轴对称的性质很容易得到 , 根据全等三角形的性质得出 , 很容易证出 , 根据相似三角形对应边成比例得出 , 利用比例式建立方程求解算出AF的长,在 中,由勾股定理建立方程,求解即可。
8.【答案】 A
【解析】【解答】解:①正确.∵A在反比例函数 的图象上,P在反比例函数 的图象上,
∴S△AOD= |m|,S△poc= |k|,
∵PC⊥OQ于点C,AD⊥OQ于点D,
∴AD∥PC,
∴△AOD∽△POC,
∴ ,
∴ 为定值,
∵△OPQ是以P为顶点的等腰三角形,
∴OP=PQ,
∴ 为定值;故此选项正确; ②正确,
∵ ,k=4m,
∴ ,
∴ ,故此选项正确;
③正确,延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ, ∴S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE= m,
∵S△PCQ=S△POC= k,
∴S△PEB=S△PCQ-S四边形CQBE= k m= ,故此选项正确; ④正确,
∵BE∥OQ,
∴△PEB∽△PCQ,
∴ ,
∵S△PCQ= k,S△PEB= , ,
∵ ,
∴ ,
∴OA2+PB2=PQ2 , 故此选项正确. 综上,选项正确的个数为4个.
故答案为:A.
【分析】①由AD∥PC易得△AOD∽△POC,由相似三角形面积之比等于相似比的平方、等腰三角形的性质和k的几何意义可得结果;②由①可得结果;③延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ,可得S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE= m,可得结果;④由BE∥OQ易得△PEB∽△PCQ,由相似三角形面积之比等于相似比的平方可得结果.
9.【答案】 D
【解析】【解答】当 时, ,当 时, ,
∴ .
连接AB并延长AB交x轴于点 ,当P在 位置时, ,即此时 的值最大.
设直线AB的解析式为 ,
将 代入解析式中得
解得 ,
∴直线AB解析式为 .
当 时, ,即 ,
.
故答案为:D.
【分析】先根据反比例函数解析式求出A,B的坐标,然后连接AB并延长AB交x轴于点P’,当P在P'位置时,PA- PB= 4B ,即此时|AP - BP|的值最大,利用待定系数法求出线AB的解析式,从而求出P'的坐标,进而利用面积公式求面积即可.
10.【答案】 C
【解析】【解答】解:①由图象可知: ,
∴ ,故正确;
②从图象上观察可得,不等式 的解集是 或 ,故错误;
④将 , 两点代入 得: ,
即: ,则 ,故正确;
③将 , 代入 得:
,解得: ,
∵ ,
∴ ,
令 ,解得: ,
令 ,解得: ,
∴ , , , ,
∴ , , ,故正确;
∴正确的有:①③④
故答案为:C.
【分析】利用函数图象可知 , 可对①作出判断;由点A,B的横坐标,观察函数图象可得到不等式 的解集,可对②作出判断;将点A,B的坐标代入两函数解析式,可得到 , 可对④作出判断;同时可得到 , 由x=0求出对应的y的值,由y=0求出对应的x的值,可得到点P,Q的坐标,即可得到OQ,OP的长;然后利用三角形的面积公式分别求出△AOP和△BOQ的面积,比较大小,可对③作出判断;综上所述可得到正确结论的序号.
二、填空题
11.【答案】 答案不唯一
【解析】【解答】解: 图象经过点A(2,3),
反比例函数
当x=-2时,
P点坐标为
故答案为: .
【分析】先求出反比例函数 , 再求点的坐标即可。
12.【答案】 (-1,-3)
【解析】【解答】∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(1,3)关于原点对称,即:该点的坐标为(﹣1,﹣3)
故答案为(﹣1,﹣3)
【分析】由反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,根据关于原点对称点坐标特征:横、纵坐标分别互为相反数,据此解答即可.
13.【答案】 36
【解析】【解答】解: 的横坐标为2,且在 的图象上,
轴,
在 的图象上,
(不合题意舍去),
故答案为:
【分析】将x=2代入反比例函数解析式可求出y的值,可得点A的坐标,由此可得到点C的坐标,再表示出BC,AC的长,由此可得到点B的坐标,然后将点B的坐标代入反比例函数解析式,建立关于k的方程,解方程求出k的值.
14.【答案】
【解析】【解答】∵点( , ),(2, ),(3, )均在反比例函数 的图象上,
∴ , , ,
∴ .
故答案为: .
【分析】画出函数的草图,结合反比例函数的性质求解即可。
15.【答案】 -4
【解析】【解答】解:连接OA
∵AB⊥y,BC∥AD
∴四边形ABCD为平行四边形
∵平行四边形ABCDA的面积为4,即AB×OB=4
∴S△AOB=AB×OB=2=|k|
∴k=-4或k=4(舍去)
【分析】根据题意即可得到四边形ABCD为平行四边形,根据平行四边形的面积为4,即可得到直角三角形AOB的面积为2,根据反比例函数的k的几何意义求出答案即可。
16.【答案】
【解析】【解答】解:设 的边 边上的高为hn , 的边 的高为hn+1 ,
则:hn+hn+1= =1,
根据题意,得: , ,
∵ ∥ ,
∴ ∽ ,
∴ ,
∴ ,
∵hn+hn+1=1,
∴ ,
∴ ,
故答案为: .
【分析】设 的边 边上的高为hn, 的边 的高为hn+1 , 可得hn+hn+1= =1,根据反比例函数的性质,可得 , , 根据相似三角形的判定与性质可得 , 利用计算即得.
三、解答题
17.【答案】 解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
18.【答案】 (1)解: 轴
在 中,
点 在函数 的图象上,
则反比例函数解析式为
在反比例函数 的图象上,
,
将 , 代入 得
代入一次函数解析式得:
解得
则一次函数解析式为
(2)解:当 时,得到 ,即
当 ,即 , ;
当 时, 是线段 的垂直平分线与 轴的交点,
(此处可用两种方法求点 )
方法一:由 得直线 的解析式为 ,线段 中点的坐标为
垂直平分线方程为 ,则
方法二:令垂足为 ,则可证 , ,
即 ,
则
综合可得, 是等腰三角形, 点坐标为 或 或 或
【解析】【分析】(1)根据勾股定理可得OD=3,再利用待定系数法求函数解析式即可;
(2)根据 是等腰三角形 ,分类讨论,结合图象作图求点的坐标即可。
19.【答案】 (1)解:∵点A的横坐标是﹣2,B点的横坐标是4,
∴当x=﹣2时,y=﹣(﹣2)+2=4,
当x=4时,y=﹣4+2=﹣2,
∴A(﹣2,4),B(4,﹣2),
∵反比例函数y= 的图象经过A,B两点,
∴k=﹣2×4=﹣8,
∴反比例函数的解析式为y=﹣ .
(2)解:一次函数y=﹣x+2中,令y=0,则x=2,
∴M(2,0),
即MO=2,
∴△AOM的面积= ×OM×|yA|= ×2×4=4.
(3)解:∵A(﹣2,4),B(4,﹣2),
∴由图象可得,反比例函数值大于一次函数值时x的取值范围为:﹣2<x<0或x>4。
【解析】【分析】(1)将点A、B的横坐标带入一次函数解析式,可计算出y值,将其代入反比例函数可得出反比例函数解析式。
(2)求出M的坐标,可得出OM的长度为2,利用面积公式可求出△AOM的面积。
(3)根据图像,在同一个x值时一次函数图像在反比例函数上方,即为x的取值范围。
20.【答案】 (1)解:∵BM⊥x轴,
∴∠BMO=90°,
∴ ,
∵BM=OM,OB=2 ,
∴ ,
∴BM=OM=2,
∴B(-2,-2)
将点B的坐标代入反比例函数 中,得k=4,
∴反比例函数解析式为 ,
将x=4代入 ,得y=1,
∴A(1,4),
将点A、B的坐标代入一次函数y=mx+n中,得 ,
解得 ,
∴一次函数的解析式为y=2x+2;
(2)解:由图象知,当-21时,
(3)解:存在.过点A作AD⊥x轴于D,
∵一次函数y=2x+2与y轴交点为C(0,2),
∴OC=2,
∴SMBOC= ,
∴ S△PAO= SMBOC=2,
∴ .
∴OP=1,
∴P(1,0)或(-1,0).
【解析】【分析】(1)根据垂直的概念可得∠BMO=90°,结合勾股定理可得BM=OM=2,则B(-2,-2),代入中可得k的值,据此可得反比例函数的解析式,将x=4代入 , 得y=1,则A(1,4),然后利用待定系数法就可求出一次函数的解析式;
(2)根据图象,找出一次函数在反比例函数图象上方部分所对应的x的范围即可;
(3)过点A作AD⊥x轴于D,易得OC=2,根据S四边形MBOC=S△AOC+S△BMO可得四边形MBOC的面积,进而求出△PAO的面积,然后根据三角形的面积公式可得OP,据此可得点P的坐标.
21.【答案】 (1)解:设P(a,b),则OA=a,
∵ ,
∴OC= AC,
∴C( a,0),
∵点C在直线y=kx+3上,
∴0= ak+3,即ka=﹣9,
∴DB=3﹣b=3﹣(ka+3)=﹣ka=9,
∵BP=a,
∴S△DBP= ×DB BP=27,
∴ ×9a=27,
∴a=6,
∴k=﹣ ,
∴一次函数的表达式为y=﹣ x+3;
将x=6代入一次函数解析式得:y=﹣6,即P(6,﹣6),
∴AP=6,
由一次函数表达式得:点D(0,3),故OD=3;
(2)解:将点P的坐标代入反比例解析式得:m2﹣13m=﹣36,
解得:m=4或9;
(3)(4,﹣6)或(10,﹣6)或(±2 ,﹣6)
【解析】【解答】解:(3)由(1)得,点C(2,0)、而点B(0,﹣6),设点M(m , ﹣6);
则BC2=4+36=40,CM2=(m﹣2)2+36,MB2=m2 ,
当BC=CM时,40=(m﹣2)2+36,解得:m=4或0(舍去0);
当BC=MB时,同理可得:m=±2 ;
当MB=CM时,同理可得:m=10,
故点M的坐标为(4,﹣6)或(10,﹣6)或(±2 ,﹣6).
【分析】(1) 设P(a,b),则OA=a,由可得点 C( a,0), 将点C代入直线y=kx+3中,可得ka=﹣9,从而求出DB=3-b=9,,根据S△DBP= ×DB BP=27可求出a值,从而求出k值即得 一次函数的表达式 ,从而求出D的坐标,即得OD的长;将x=6代入求出y值即得点P坐标,即可得出AP的长;
(2)由(1)知点P(6,-6),将其代入 y2= (x>0) 中,即可求出m值;
(3)设点M(m , ﹣6),根据等腰三角形的判定分三种情况:①当BC=CM时,②当BC=MB时,③当MB=CM时,据此分别建立方程求出m值即可
一、单选题
1.(2020九上·灌阳期中)下列各点中,在反比例函数 图象上的是( )
A. (-1,8) B. (-2,4) C. (1,7) D. (2,4)
2.下列选项,是反比例函数关系的为( )
A. 在直角三角形中,30°角所对的直角边 与斜边 之间的关系
B. 在等腰三角形中,顶角 与底角 之间的关系
C. 圆的面积 与它的直径 之间的关系
D. 面积为20的菱形,其中一条对角线 与另一条对角线 之间的关系
3.(2019九上·陵县月考)已知函数y=(m+2)x 是反比例函数,则m的值是( )
A. 2 B. C. D.
4.(2019九上·双台子月考)如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为( )
A. 4 B. ﹣4 C. 8 D. ﹣8
5.(2020九上·历下期中)已知点A(﹣1,y1)、B(﹣2,y2)、C(3,y3)都在反比例函数y= 的图象上,则y1、y2、y3的关系是( )
A. y2>y1>y3 B. y2>y3>y1 C. y3>y1>y2 D. y3>y2>y1
6.(2020·南岸模拟)如图所示,直线y1=﹣ x与双曲线y= 交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
A. ﹣10 B. ﹣9 C. 6 D. 4
7.(2019·十堰)如图,平面直角坐标系中, ,反比例函数 的图象分别与线段 交于点 ,连接 .若点 关于 的对称点恰好在 上,则 ( )
A. B. C. D.
8.(2021·九龙坡模拟)如图,在第一象限内,动点P在反比例函数y= 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y= 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
① 为定值;②若k=4m,则A为OP中点;③S△PEB= ;④OA2+PB2=PQ2.
A. 4 B. 3 C. 2 D. 1
9.(2021八下·淮阴期末)如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( )
A. B. 1 C. D.
10.(2021八下·遂宁期末)如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A. ①③ B. ②③④ C. ①③④ D. ②④
二、填空题
11.(2021九上·玉屏侗族自治期中)如图,反比例函数 的图象位于第一、三象限,其中第一象限内的图象经过点A(2,3),请在第三象限内的图象上找一个你喜欢的点P , 你选择的P点坐标为 .
12.(2020·江夏模拟)已知一个正比例函数的图象与一个反比例函数图象的一个交点坐标为(1,3),则另一个交点坐标是________.
13.(2021·玄武模拟)如图,点 , 在反比例函数 的图象上,点 在反比例函数 的图象上,连接 , ,且 轴, 轴, .若点 的横坐标为2,则 的值为 .
14.(2020九上·迎泽月考)已知点( , ),( , ),( , )均在反比例函数 的图象上,则 , , 的大小关系是________.(用“<”连接)
15.(2020九上·通榆月考)如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k=________ 。
16.(2020九上·丹东月考)如图,分别过x轴上的点 作x轴的垂线,与反比例函数 图象的交点分别为 与 相交于点 与 相交于点 ,…, 与 相交于点 ,若 的面积记为 , 的面积记为 , 的面积记为 ,… 的面积记为 ,则 =________
三、解答题
17.(2021·青田模拟)如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
18.(2020九上·株洲期中)如图所示,在平面直角坐标系中,一次函数 与反比例函数 的图像交于第二、四象限 、 两点,过点 作 轴于点 , , ,且点 的坐标为 .
(1)求一次函数与反比例函数的解析式.
(2) 是 轴上一点,且 是等腰三角形,请直接写出所有符合条件的 点坐标.
19.(2019九上·荔湾期末)如图,已知一次函数y=﹣x+2与反比例函数y= 与的图象交于A,B两点,与x轴交于点M,且点A的横坐标是﹣2,B点的横坐标是4.
(1)求反比例函数的解析式;
(2)求△AOM的面积;
(3)根据图象直接写出反比例函数值大于一次函数值时x的取值范围.
20.(2021九上·通川期中)如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数 (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2 ,点A的纵坐标为4.
(1)求一次函数的解析式;
(2)求不等式mx+n> 的解集;
(3)连接MC,AO在x轴上,是否存在点P使S△PAO= SMBOC , 若存在,求出P点坐标,若不存在,请说明理由.
21.(2021·深圳模拟)如图1,直线y1=kx+3与双曲线y2= (x>0)交于点P , PA⊥x轴于点A , PB⊥y轴于点B , 直线y1=kx+3分别交x轴、y轴于点C和点D , 且S△DBP=27, .
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM , 当△BCM为等腰三角形时,请直接写出点M的坐标.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解:A、∵-1×8=-8≠8,∴该点不在函数图象上,故本选项错误;
B、∵-2×4=-8≠8,∴该点不在函数图象上,故本选项错误;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项错误;
D、2×4=8,∴该点在函数图象上,故本选项正确.
故答案为:D.
【分析】由于反比例函数y= 中,k=xy,即将各选项横、纵坐标分别相乘,其积为8者即为正确答案.
2.【答案】 D
【解析】【解答】解:A、由题意可知:y= , 是正比例函数关系,此选项不符合题意;
B、由题意可知 :y=180°-2x,是一次函数关系,此选项不符合题意;
C、由题意可知 :S=,是二次函数关系,此选项不符合题意;
D、由题意可知:是反比例函数关系,此选项符合题意;
故答案为 :D。
【分析】A、根据含30°直角三角形的斜边等于 30°角所对的直角边 的2倍,列出函数关系,根据函数特点即可判断出该函数是正比例函数关系,此选项不符合题意;
B、根据等腰三角形的两底角相等,及三角形的内角和定理即可建立出函数关系,根据函数特点即可判断出该函数是一次函数关系,此选项不符合题意;
C、根据圆的面积等于r2即可列出函数关系式,根据函数特点即可判断出该函数是二次函数关系,此选项不符合题意;
D、根据菱形的面积等于两对角线乘积的一半,即可列出函数关系式,根据函数特点即可判断出该函数是反比例函数关系,此选项符合题意。
3.【答案】 A
【解析】【解答】解:依题意得:m2-5=-1,且m+2≠0,
解得m=2.
故答案为:A .
【分析】根据反比例函数的定义得到m2-5=-1,且m+2≠0,由此求得m的值.
4.【答案】 D
【解析】【解答】解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴ ,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y= 的图象上,则mn=2,
∵点B在反比例函数y= 的图象上,
∴B点的坐标是( 2n,2m),
∴k= 2n 2m= 4mn= 8.
故答案为:D.
【分析】求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,根据条件得到△ACO∽△ODB,得到 ,然后用待定系数法即可.
5.【答案】 D
【解析】【解答】解:∵在反比例函数y= 中,k=1>0,
∴此函数图象在一、三象限,
∵﹣2<﹣1<0,
∴点A(﹣1,y1),B(﹣2,y2)在第三象限,
∴y1<y2<0,
∵3>0,
∴C(3,y3)点在第一象限,
∴y3>0,
∴y1 , y2 , y3的大小关系为y3>y2>y1 .
故答案为:D.
【分析】先根据函数解析式中的比例系数K,确定函数图像所在的象限,在根据各象限内点的坐标,特征及函数的增减性解答即可。
6.【答案】 B
【解析】【解答】解:∵直线y1=﹣ x与双曲线y= 交于A,B两点,
∴点A与点B关于原点对称,OA=OB,
∵AC⊥BC,
∴∠ACB=90°,
∴OA=OB=OC,
设A(t,﹣ t),则B(﹣t, t),
∴OA= =﹣ t,
∴OC=﹣ t,
∵S△ABC=15,
∴ ×(﹣ t)(﹣ t﹣ )=15,解得t=﹣ ,
∴A(﹣ ,2 ),
把A(﹣ ,2 )代入y= 得k=﹣ ×2 =﹣9.
故答案为:B.
【分析】先根据正比例函数和反比例函数的性质得到点 与点 关于原点对称, ,再根据直角三角形斜边上的中线性质得到 ,设 ,则 ,利用勾股定理表示出 ,则 ,接着利用三角形面积公式得到 ,解出 得到 , ,然后把 , 代入 中可求出 的值.
7.【答案】 C
【解析】【解答】解:过点 作 ,垂足为 ,设点 关于 的对称点为 ,连接 ,如图所示:
则 ,
易证
,
,
,
在反比例函数 的图象上,
,
在 中,由勾股定理:
即:
解得: 。
故答案为:C。
【分析】过点 作 ,垂足为 ,设点 关于 的对称点为 ,连接 ,如图所示:根据A,B,C三点的坐标特点得出 , 根据点的坐标与图形的性质分别用含k的式子表示出点D,E的坐标,根据轴对称的性质很容易得到 , 根据全等三角形的性质得出 , 很容易证出 , 根据相似三角形对应边成比例得出 , 利用比例式建立方程求解算出AF的长,在 中,由勾股定理建立方程,求解即可。
8.【答案】 A
【解析】【解答】解:①正确.∵A在反比例函数 的图象上,P在反比例函数 的图象上,
∴S△AOD= |m|,S△poc= |k|,
∵PC⊥OQ于点C,AD⊥OQ于点D,
∴AD∥PC,
∴△AOD∽△POC,
∴ ,
∴ 为定值,
∵△OPQ是以P为顶点的等腰三角形,
∴OP=PQ,
∴ 为定值;故此选项正确; ②正确,
∵ ,k=4m,
∴ ,
∴ ,故此选项正确;
③正确,延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ, ∴S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE= m,
∵S△PCQ=S△POC= k,
∴S△PEB=S△PCQ-S四边形CQBE= k m= ,故此选项正确; ④正确,
∵BE∥OQ,
∴△PEB∽△PCQ,
∴ ,
∵S△PCQ= k,S△PEB= , ,
∵ ,
∴ ,
∴OA2+PB2=PQ2 , 故此选项正确. 综上,选项正确的个数为4个.
故答案为:A.
【分析】①由AD∥PC易得△AOD∽△POC,由相似三角形面积之比等于相似比的平方、等腰三角形的性质和k的几何意义可得结果;②由①可得结果;③延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ,可得S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE= m,可得结果;④由BE∥OQ易得△PEB∽△PCQ,由相似三角形面积之比等于相似比的平方可得结果.
9.【答案】 D
【解析】【解答】当 时, ,当 时, ,
∴ .
连接AB并延长AB交x轴于点 ,当P在 位置时, ,即此时 的值最大.
设直线AB的解析式为 ,
将 代入解析式中得
解得 ,
∴直线AB解析式为 .
当 时, ,即 ,
.
故答案为:D.
【分析】先根据反比例函数解析式求出A,B的坐标,然后连接AB并延长AB交x轴于点P’,当P在P'位置时,PA- PB= 4B ,即此时|AP - BP|的值最大,利用待定系数法求出线AB的解析式,从而求出P'的坐标,进而利用面积公式求面积即可.
10.【答案】 C
【解析】【解答】解:①由图象可知: ,
∴ ,故正确;
②从图象上观察可得,不等式 的解集是 或 ,故错误;
④将 , 两点代入 得: ,
即: ,则 ,故正确;
③将 , 代入 得:
,解得: ,
∵ ,
∴ ,
令 ,解得: ,
令 ,解得: ,
∴ , , , ,
∴ , , ,故正确;
∴正确的有:①③④
故答案为:C.
【分析】利用函数图象可知 , 可对①作出判断;由点A,B的横坐标,观察函数图象可得到不等式 的解集,可对②作出判断;将点A,B的坐标代入两函数解析式,可得到 , 可对④作出判断;同时可得到 , 由x=0求出对应的y的值,由y=0求出对应的x的值,可得到点P,Q的坐标,即可得到OQ,OP的长;然后利用三角形的面积公式分别求出△AOP和△BOQ的面积,比较大小,可对③作出判断;综上所述可得到正确结论的序号.
二、填空题
11.【答案】 答案不唯一
【解析】【解答】解: 图象经过点A(2,3),
反比例函数
当x=-2时,
P点坐标为
故答案为: .
【分析】先求出反比例函数 , 再求点的坐标即可。
12.【答案】 (-1,-3)
【解析】【解答】∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(1,3)关于原点对称,即:该点的坐标为(﹣1,﹣3)
故答案为(﹣1,﹣3)
【分析】由反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,根据关于原点对称点坐标特征:横、纵坐标分别互为相反数,据此解答即可.
13.【答案】 36
【解析】【解答】解: 的横坐标为2,且在 的图象上,
轴,
在 的图象上,
(不合题意舍去),
故答案为:
【分析】将x=2代入反比例函数解析式可求出y的值,可得点A的坐标,由此可得到点C的坐标,再表示出BC,AC的长,由此可得到点B的坐标,然后将点B的坐标代入反比例函数解析式,建立关于k的方程,解方程求出k的值.
14.【答案】
【解析】【解答】∵点( , ),(2, ),(3, )均在反比例函数 的图象上,
∴ , , ,
∴ .
故答案为: .
【分析】画出函数的草图,结合反比例函数的性质求解即可。
15.【答案】 -4
【解析】【解答】解:连接OA
∵AB⊥y,BC∥AD
∴四边形ABCD为平行四边形
∵平行四边形ABCDA的面积为4,即AB×OB=4
∴S△AOB=AB×OB=2=|k|
∴k=-4或k=4(舍去)
【分析】根据题意即可得到四边形ABCD为平行四边形,根据平行四边形的面积为4,即可得到直角三角形AOB的面积为2,根据反比例函数的k的几何意义求出答案即可。
16.【答案】
【解析】【解答】解:设 的边 边上的高为hn , 的边 的高为hn+1 ,
则:hn+hn+1= =1,
根据题意,得: , ,
∵ ∥ ,
∴ ∽ ,
∴ ,
∴ ,
∵hn+hn+1=1,
∴ ,
∴ ,
故答案为: .
【分析】设 的边 边上的高为hn, 的边 的高为hn+1 , 可得hn+hn+1= =1,根据反比例函数的性质,可得 , , 根据相似三角形的判定与性质可得 , 利用计算即得.
三、解答题
17.【答案】 解:把点 代入
当 时,
把 , 代入y1=kx+b
,
①-②得,
把 代入①得,
即
.
【解析】【分析】先把A点坐标代入 y2= ,求出反比例函数解析式,接着把 代入反比例函数求出B点坐标,最后把A、B两点坐标代入一次函数 y1=kx+b ,解出k、b即可得到一次函数解析式.
18.【答案】 (1)解: 轴
在 中,
点 在函数 的图象上,
则反比例函数解析式为
在反比例函数 的图象上,
,
将 , 代入 得
代入一次函数解析式得:
解得
则一次函数解析式为
(2)解:当 时,得到 ,即
当 ,即 , ;
当 时, 是线段 的垂直平分线与 轴的交点,
(此处可用两种方法求点 )
方法一:由 得直线 的解析式为 ,线段 中点的坐标为
垂直平分线方程为 ,则
方法二:令垂足为 ,则可证 , ,
即 ,
则
综合可得, 是等腰三角形, 点坐标为 或 或 或
【解析】【分析】(1)根据勾股定理可得OD=3,再利用待定系数法求函数解析式即可;
(2)根据 是等腰三角形 ,分类讨论,结合图象作图求点的坐标即可。
19.【答案】 (1)解:∵点A的横坐标是﹣2,B点的横坐标是4,
∴当x=﹣2时,y=﹣(﹣2)+2=4,
当x=4时,y=﹣4+2=﹣2,
∴A(﹣2,4),B(4,﹣2),
∵反比例函数y= 的图象经过A,B两点,
∴k=﹣2×4=﹣8,
∴反比例函数的解析式为y=﹣ .
(2)解:一次函数y=﹣x+2中,令y=0,则x=2,
∴M(2,0),
即MO=2,
∴△AOM的面积= ×OM×|yA|= ×2×4=4.
(3)解:∵A(﹣2,4),B(4,﹣2),
∴由图象可得,反比例函数值大于一次函数值时x的取值范围为:﹣2<x<0或x>4。
【解析】【分析】(1)将点A、B的横坐标带入一次函数解析式,可计算出y值,将其代入反比例函数可得出反比例函数解析式。
(2)求出M的坐标,可得出OM的长度为2,利用面积公式可求出△AOM的面积。
(3)根据图像,在同一个x值时一次函数图像在反比例函数上方,即为x的取值范围。
20.【答案】 (1)解:∵BM⊥x轴,
∴∠BMO=90°,
∴ ,
∵BM=OM,OB=2 ,
∴ ,
∴BM=OM=2,
∴B(-2,-2)
将点B的坐标代入反比例函数 中,得k=4,
∴反比例函数解析式为 ,
将x=4代入 ,得y=1,
∴A(1,4),
将点A、B的坐标代入一次函数y=mx+n中,得 ,
解得 ,
∴一次函数的解析式为y=2x+2;
(2)解:由图象知,当-2
(3)解:存在.过点A作AD⊥x轴于D,
∵一次函数y=2x+2与y轴交点为C(0,2),
∴OC=2,
∴SMBOC= ,
∴ S△PAO= SMBOC=2,
∴ .
∴OP=1,
∴P(1,0)或(-1,0).
【解析】【分析】(1)根据垂直的概念可得∠BMO=90°,结合勾股定理可得BM=OM=2,则B(-2,-2),代入中可得k的值,据此可得反比例函数的解析式,将x=4代入 , 得y=1,则A(1,4),然后利用待定系数法就可求出一次函数的解析式;
(2)根据图象,找出一次函数在反比例函数图象上方部分所对应的x的范围即可;
(3)过点A作AD⊥x轴于D,易得OC=2,根据S四边形MBOC=S△AOC+S△BMO可得四边形MBOC的面积,进而求出△PAO的面积,然后根据三角形的面积公式可得OP,据此可得点P的坐标.
21.【答案】 (1)解:设P(a,b),则OA=a,
∵ ,
∴OC= AC,
∴C( a,0),
∵点C在直线y=kx+3上,
∴0= ak+3,即ka=﹣9,
∴DB=3﹣b=3﹣(ka+3)=﹣ka=9,
∵BP=a,
∴S△DBP= ×DB BP=27,
∴ ×9a=27,
∴a=6,
∴k=﹣ ,
∴一次函数的表达式为y=﹣ x+3;
将x=6代入一次函数解析式得:y=﹣6,即P(6,﹣6),
∴AP=6,
由一次函数表达式得:点D(0,3),故OD=3;
(2)解:将点P的坐标代入反比例解析式得:m2﹣13m=﹣36,
解得:m=4或9;
(3)(4,﹣6)或(10,﹣6)或(±2 ,﹣6)
【解析】【解答】解:(3)由(1)得,点C(2,0)、而点B(0,﹣6),设点M(m , ﹣6);
则BC2=4+36=40,CM2=(m﹣2)2+36,MB2=m2 ,
当BC=CM时,40=(m﹣2)2+36,解得:m=4或0(舍去0);
当BC=MB时,同理可得:m=±2 ;
当MB=CM时,同理可得:m=10,
故点M的坐标为(4,﹣6)或(10,﹣6)或(±2 ,﹣6).
【分析】(1) 设P(a,b),则OA=a,由可得点 C( a,0), 将点C代入直线y=kx+3中,可得ka=﹣9,从而求出DB=3-b=9,,根据S△DBP= ×DB BP=27可求出a值,从而求出k值即得 一次函数的表达式 ,从而求出D的坐标,即得OD的长;将x=6代入求出y值即得点P坐标,即可得出AP的长;
(2)由(1)知点P(6,-6),将其代入 y2= (x>0) 中,即可求出m值;
(3)设点M(m , ﹣6),根据等腰三角形的判定分三种情况:①当BC=CM时,②当BC=MB时,③当MB=CM时,据此分别建立方程求出m值即可
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
