2021-2022学年鲁教版(五四制)七年级上学期数学期末练习试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级上学期数学期末练习试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 22:51:04 | ||
图片预览



文档简介
2021-2022学年鲁教五四新版七年级上学期数学期末练习试卷一.选择题(共12小题,满分36分,每小题3分)
1.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
2.下列各数中是无理数的是( )
A. B. C. D.
3.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2、3、4 B.、、 C.5、12、13 D.30、50、60
4.一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为t,剩下的水量为s.下面能反映s与t之间的关系的大致图象是( )
A. B.
C. D.
5.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M、N,再分别以M、N为圆心,大于MN为半径画弧,两弧交于点G,作射线AG交BC于点D.已知BD=5,CD=3,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.5 D.8
6.若|x|=2017,则x等于( )
A.﹣2017 B.2017 C. D.±2017
7.如图,点A、D、C、F在同一条直线上,若AB=DE,BC=EF,则下列条件中能满足△ABC≌△DEF的是( )
A.∠A=∠EDF B.AD=CF C.∠BCA=∠F D.BC∥EF
8.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
9.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
10.在平面直角坐标系中,将函数y=2x﹣1的图象向左平移1个单位长度,则平移后的图象与y轴的交点坐标为( )
A.(0,2) B.(0,﹣2) C.(0,1) D.(0,﹣1)
11.如图,等腰直角三角形ABC与等腰直角三角形A1B1C1均位于第一象限内,它们的直角边平行于x轴或y轴,其中点A、A1在直线OM上,点C、C1在直线ON上,O为坐标原点,已知点A的坐标为(3,3),AB=1,若A1B1=2,则点B1的坐标为( )
A.(2,4) B.(4,6) C.(6,8) D.(8,10)
12.如图,在Rt△ABC中,∠ABC=90°,BC=12,AB=5.分别以A,C为圆心,以大于线段AC长度的一半为半径作弧,两弧相交于点E,F,过点E,F作直线EF,交AC于点D,连接BD,则△ABD的周长为( )
A.13 B.17 C.18 D.25
二.填空题(共6小题,满分18分,每小题3分)
13.比较实数大小:﹣3 ﹣2(填“>”或“<”).
14.一个正数a的平方根分别是2m﹣1和﹣3m+,则这个正数a为 .
15.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,AC=3,则BD的长是 .
16.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
17.等腰三角形的腰长为13,底边长为10,则顶角的平分线长为 .
18.如图,已知在△ABC中,D,E分别为边BC,AD的中点,且S阴影面积=10,则S△ABC等于 .
三.解答题(共7小题,满分66分)
19.已知:y﹣2与x成正比例,且x=2时,y=4.
(1)求y关于x的函数表达式;
(2)若点M(m,3)在这个函数的图象上,求点M的坐标.
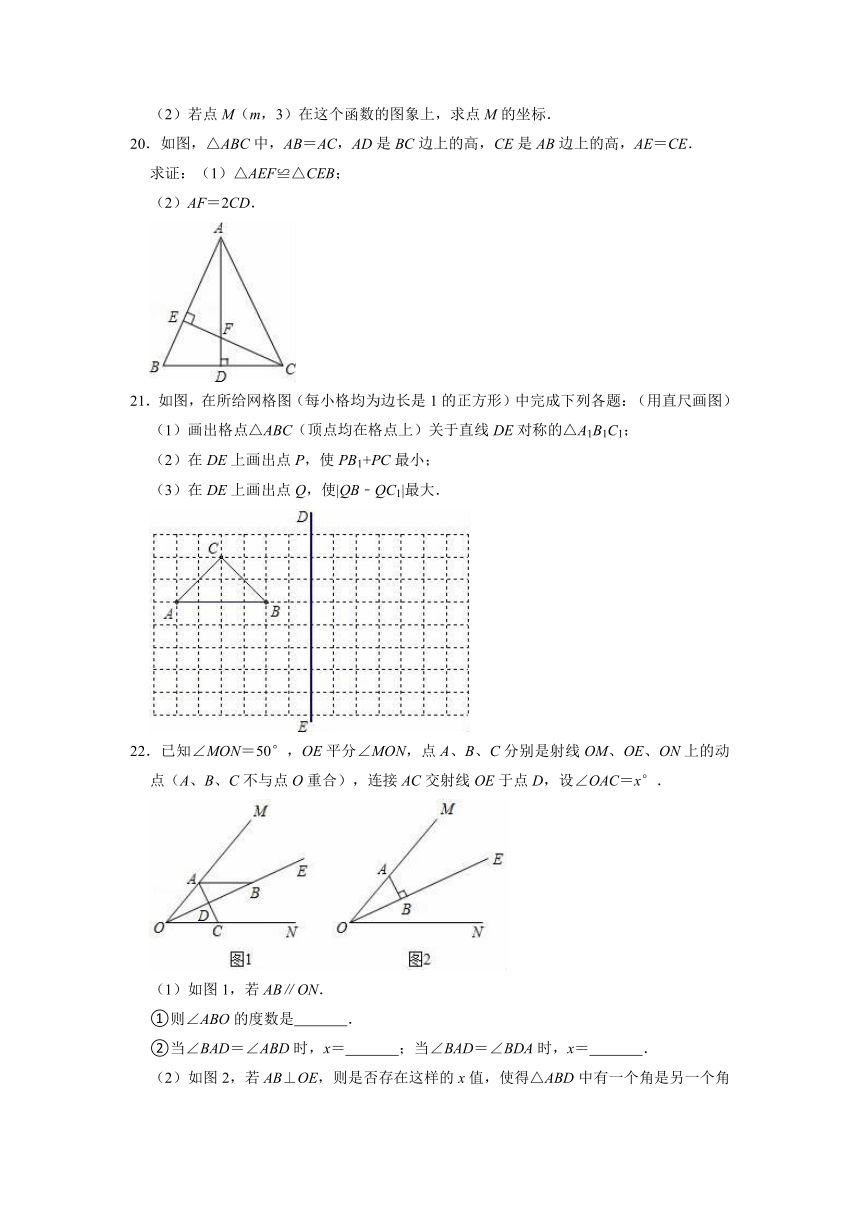
20.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
21.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使|QB﹣QC1|最大.
22.已知∠MON=50°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D,设∠OAC=x°.
(1)如图1,若AB∥ON.
①则∠ABO的度数是 .
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OE,则是否存在这样的x值,使得△ABD中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
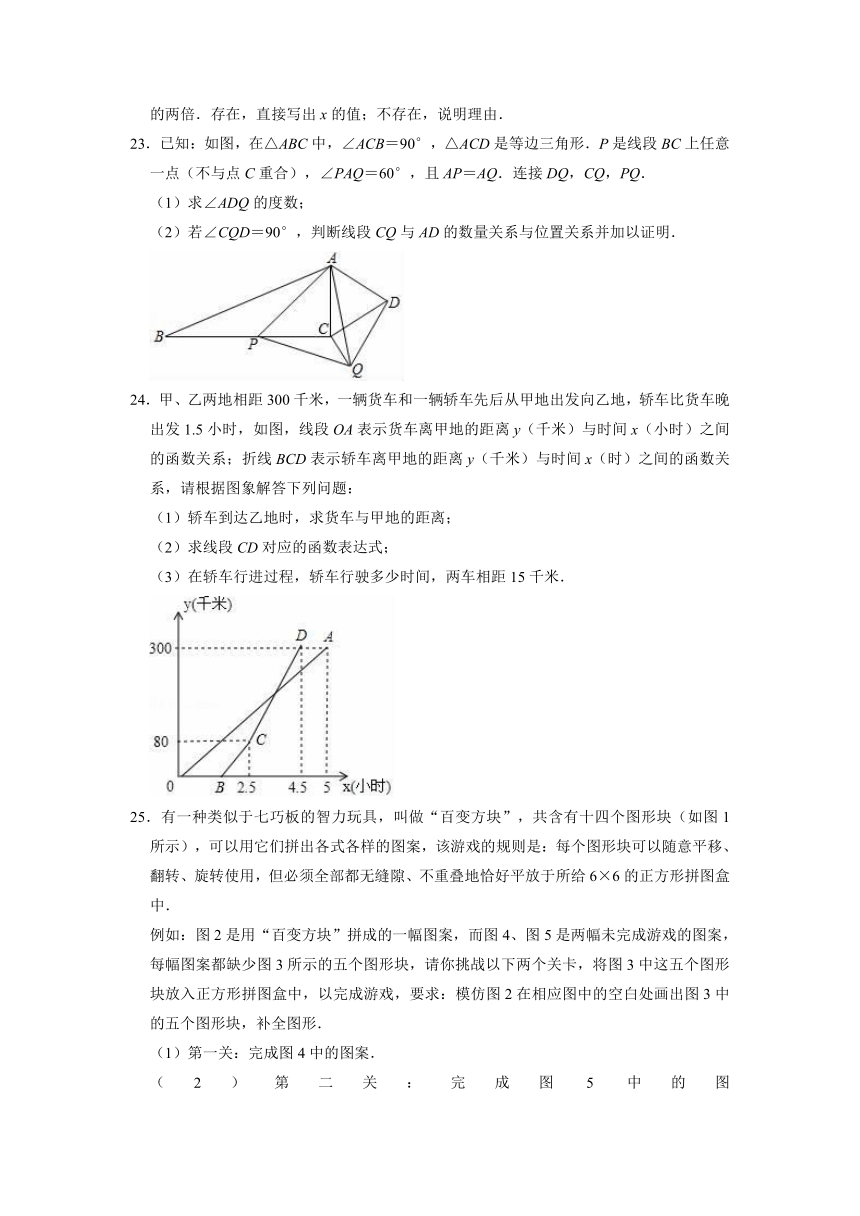
23.已知:如图,在△ABC中,∠ACB=90°,△ACD是等边三角形.P是线段BC上任意一点(不与点C重合),∠PAQ=60°,且AP=AQ.连接DQ,CQ,PQ.
(1)求∠ADQ的度数;
(2)若∠CQD=90°,判断线段CQ与AD的数量关系与位置关系并加以证明.
24.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
25.有一种类似于七巧板的智力玩具,叫做“百变方块”,共含有十四个图形块(如图1所示),可以用它们拼出各式各样的图案,该游戏的规则是:每个图形块可以随意平移、翻转、旋转使用,但必须全部都无缝隙、不重叠地恰好平放于所给6×6的正方形拼图盒中.
例如:图2是用“百变方块”拼成的一幅图案,而图4、图5是两幅未完成游戏的图案,每幅图案都缺少图3所示的五个图形块,请你挑战以下两个关卡,将图3中这五个图形块放入正方形拼图盒中,以完成游戏,要求:模仿图2在相应图中的空白处画出图3中的五个图形块,补全图形.
(1)第一关:完成图4中的图案.
(2)第二关:完成图5中的图案.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.解:符合无理数的概念,故选项A符合题意;
是有理数,故选项B不符合题意;
=﹣2是有理数,故选项C不符合题意;
=是有理数,故选项B不符合题意.
故选:A.
3.解:A、22+32≠42,不能构成直角三角形,故此选项不符合题意;
B、()2+()2≠()2,不能构成直角三角形,故此选项不符合题意;
C、52+122=132,能构成直角三角形,故此选项符合题意;
D、302+502≠602,不能构成直角三角形,故此选项不符合题意.
故选:C.
4.解:由题意,随着抽水时间的增加,剩下的水量逐渐减少;停止时剩下的水量不变,两台抽水机同时工作抽水速度增大,剩下的水量迅速减少,可得答案.
故选:D.
5.解:由作法得AD平分∠BAC,
∴点D到AB的距离=CD=3,
∴PD的最小值为3.
故选:B.
6.解:∵|±7|=2017,|x|=2017,
∴x=±2017.
故选:D.
7.解:∵AB=DE,BC=EF,
∴添加∠B=∠E或AD=CF或AC=DF,即可证明△ABC≌△DEF.
故选:B.
8.解:在Rt△ABC中,AC==4米,
故可得地毯长度=AC+BC=7米,
故选:D.
9.解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
∴点C的坐标为(3,2),线段的最小值为2.
故选:B.
10.解:∵将函数y=2x﹣1的图象向左平移1个单位长度的解析式为y=2(x+1)﹣1=2x+1,
∴当x=0时,y=1,
∴平移后与y轴的交点坐标为(0,1),
故选:C.
11.解:∵△ABC,△A1B1C1都是等腰直角三角形,
∴AC=AB=,A1C1=A1B1=2,
∴A1C1=2AC,
由题意A1C1∥AC,
∴AC是△OA1C1的中位线,
∴OA=OA1,
∵A(3,3),
∴A1(6,6),
∵A1B1=2,A1B1∥x轴,
∴B1(4,6),
故选:B.
12.解:∵∠ABC=90°,BC=12,AB=5,
∴AC==13,
根据题意可得EF是AC的垂直平分线,
∴D是AC的中点,
∴AD=AC=6.5,BD=AC=6.5,
∴△ABD的周长为6.5+6.5+5=18.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵2<<3,2<<3,
∴﹣3<0,﹣2>0,
∴﹣3<﹣2.
故答案为:<.
14.解:根据题意,得:2m﹣1+(﹣3m+)=0,
解得:m=,
∴正数a=(2×﹣1)2=4,
故答案为:4.
15.解:过D作DE⊥AB于E,
在△ABC中,∠C=90°,AB=5,AC=3,
∴BC===4,
∵AD平分∠BAC,
∴DE=DC,
∵AC BC=AC CD+AB DE,即×3×4=×3CD+×5CD,
解得CD=1.5,
∴BD=4﹣CD=4﹣1.5=2.5.
故答案为:2.5.
16.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
17.解:根据题意,AD是∠A的平分线、BC边上的中线也是BC边上的高线,
∴BD=BC=5,∴AD==12.
故应填12.
18.解:∵E为边AD的中点,
∴S△ACD=2S阴影面积=2×10=20,
∵D为边BC的中点,
∴S△ABC=2S△ACD=2×20=40,
故答案为:40.
三.解答题(共7小题,满分66分)
19.解:(1)设y﹣2=kx,
把x=2,y=4代入求得k=1,
∴函数解析式是y=x+2;
(2)∵点M(m,3)在这个函数图象上,
∴3=m+2,
解得:m=1,
∴M(1,3).
20.证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
21.解:(1)如图,△A1B1C1即为所求作.
(2)如图,点P即为所求作.
(3)如图点Q即为所求作.
22.解:( 1 )①∠MON=50°,OE平分∠MON,
∴∠AOB=∠BON=25°,
∵AB∥ON,
∴∠ABO=25°,
故答案为25°;
②当∠BAD=∠ABD时,∠BAD=25°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠AOB+∠ABO+∠OAC+∠BAD=180°,
∴x=∠OAC=180°﹣∠AOB﹣∠ABO﹣∠BAD=180°﹣25°﹣25°﹣25°=105°,
当∠BAD=∠BDA时,
∵∠ABO=25°,
∴∠BAD=77.5°,
∴∠OAB=180°﹣∠ABO﹣∠AOB=180°﹣25°﹣35°=130°,
∴x=∠OAC=∠OAB﹣∠BAD=130°﹣77.5°=52.5°,
故答案为105°;52.5°;
(2)存在这样的∠OAC,使得△ABD中有一个角是另一个角的两倍,其x值分别为20;110;5;125;35;95.
当点D在线段OB上时,
Ⅰ当∠ABD=2∠DAB=90°时,∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=45°﹣25°=20°;
Ⅱ当∠ADB=2∠DAB时,
∵∠ABD=90°,
∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=60°﹣25°=35°;
Ⅲ当∠DAB=2∠ADB时,
∵∠ABD=90°,
∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=30°﹣25°;
当点D在线段OB延长线上时,
Ⅰ当∠ABD=2∠DAB=90°时,∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣45°﹣25°=110°;
Ⅱ当∠ADB=2∠DAB时,
∵∠ABD=90°,
∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣60°﹣25°=95°;
Ⅲ当∠DAB=2∠ADB时,
∵∠ABD=90°,
∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣30°﹣25°=125°.
综上所述,存在这样的∠OAC,使得△ABD中有一个角是另一个角的两倍.
其x值分别为20;110;5;125;35;95.
23.解:(1)∵∠PAQ=60°,
∴△ACD是等边三角形,
∴AC=AD.∠CAD=60°=∠PAQ,
∴∠PAC=∠QAD,
在△PAC和△QAD中,
,
∴△PAC≌△QAD(SAS),
∴∠ADQ=∠ACB,
∵∠ACB=90°,
∴∠ADQ=90°;
(2)线段CQ与AD的数量关系是:,
位置关系是:CQ∥AD,
∵∠ADQ=90°,∠CQD=90°,
∴∠CQD+∠ADQ=180°,
∴AD∥CQ,
∵△ACD是等边三角形,
∴CD=AD,
∴∠ADC=60°,
∴∠QDC=30°,
∴,
∴.
24.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
25.解:(1)如图4所示:
(2)如图5所示(答案不唯一):
1.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
2.下列各数中是无理数的是( )
A. B. C. D.
3.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2、3、4 B.、、 C.5、12、13 D.30、50、60
4.一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为t,剩下的水量为s.下面能反映s与t之间的关系的大致图象是( )
A. B.
C. D.
5.如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M、N,再分别以M、N为圆心,大于MN为半径画弧,两弧交于点G,作射线AG交BC于点D.已知BD=5,CD=3,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.5 D.8
6.若|x|=2017,则x等于( )
A.﹣2017 B.2017 C. D.±2017
7.如图,点A、D、C、F在同一条直线上,若AB=DE,BC=EF,则下列条件中能满足△ABC≌△DEF的是( )
A.∠A=∠EDF B.AD=CF C.∠BCA=∠F D.BC∥EF
8.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
9.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
10.在平面直角坐标系中,将函数y=2x﹣1的图象向左平移1个单位长度,则平移后的图象与y轴的交点坐标为( )
A.(0,2) B.(0,﹣2) C.(0,1) D.(0,﹣1)
11.如图,等腰直角三角形ABC与等腰直角三角形A1B1C1均位于第一象限内,它们的直角边平行于x轴或y轴,其中点A、A1在直线OM上,点C、C1在直线ON上,O为坐标原点,已知点A的坐标为(3,3),AB=1,若A1B1=2,则点B1的坐标为( )
A.(2,4) B.(4,6) C.(6,8) D.(8,10)
12.如图,在Rt△ABC中,∠ABC=90°,BC=12,AB=5.分别以A,C为圆心,以大于线段AC长度的一半为半径作弧,两弧相交于点E,F,过点E,F作直线EF,交AC于点D,连接BD,则△ABD的周长为( )
A.13 B.17 C.18 D.25
二.填空题(共6小题,满分18分,每小题3分)
13.比较实数大小:﹣3 ﹣2(填“>”或“<”).
14.一个正数a的平方根分别是2m﹣1和﹣3m+,则这个正数a为 .
15.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,AC=3,则BD的长是 .
16.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
17.等腰三角形的腰长为13,底边长为10,则顶角的平分线长为 .
18.如图,已知在△ABC中,D,E分别为边BC,AD的中点,且S阴影面积=10,则S△ABC等于 .
三.解答题(共7小题,满分66分)
19.已知:y﹣2与x成正比例,且x=2时,y=4.
(1)求y关于x的函数表达式;
(2)若点M(m,3)在这个函数的图象上,求点M的坐标.
20.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
21.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使|QB﹣QC1|最大.
22.已知∠MON=50°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D,设∠OAC=x°.
(1)如图1,若AB∥ON.
①则∠ABO的度数是 .
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OE,则是否存在这样的x值,使得△ABD中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
23.已知:如图,在△ABC中,∠ACB=90°,△ACD是等边三角形.P是线段BC上任意一点(不与点C重合),∠PAQ=60°,且AP=AQ.连接DQ,CQ,PQ.
(1)求∠ADQ的度数;
(2)若∠CQD=90°,判断线段CQ与AD的数量关系与位置关系并加以证明.
24.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
25.有一种类似于七巧板的智力玩具,叫做“百变方块”,共含有十四个图形块(如图1所示),可以用它们拼出各式各样的图案,该游戏的规则是:每个图形块可以随意平移、翻转、旋转使用,但必须全部都无缝隙、不重叠地恰好平放于所给6×6的正方形拼图盒中.
例如:图2是用“百变方块”拼成的一幅图案,而图4、图5是两幅未完成游戏的图案,每幅图案都缺少图3所示的五个图形块,请你挑战以下两个关卡,将图3中这五个图形块放入正方形拼图盒中,以完成游戏,要求:模仿图2在相应图中的空白处画出图3中的五个图形块,补全图形.
(1)第一关:完成图4中的图案.
(2)第二关:完成图5中的图案.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.解:符合无理数的概念,故选项A符合题意;
是有理数,故选项B不符合题意;
=﹣2是有理数,故选项C不符合题意;
=是有理数,故选项B不符合题意.
故选:A.
3.解:A、22+32≠42,不能构成直角三角形,故此选项不符合题意;
B、()2+()2≠()2,不能构成直角三角形,故此选项不符合题意;
C、52+122=132,能构成直角三角形,故此选项符合题意;
D、302+502≠602,不能构成直角三角形,故此选项不符合题意.
故选:C.
4.解:由题意,随着抽水时间的增加,剩下的水量逐渐减少;停止时剩下的水量不变,两台抽水机同时工作抽水速度增大,剩下的水量迅速减少,可得答案.
故选:D.
5.解:由作法得AD平分∠BAC,
∴点D到AB的距离=CD=3,
∴PD的最小值为3.
故选:B.
6.解:∵|±7|=2017,|x|=2017,
∴x=±2017.
故选:D.
7.解:∵AB=DE,BC=EF,
∴添加∠B=∠E或AD=CF或AC=DF,即可证明△ABC≌△DEF.
故选:B.
8.解:在Rt△ABC中,AC==4米,
故可得地毯长度=AC+BC=7米,
故选:D.
9.解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
∴点C的坐标为(3,2),线段的最小值为2.
故选:B.
10.解:∵将函数y=2x﹣1的图象向左平移1个单位长度的解析式为y=2(x+1)﹣1=2x+1,
∴当x=0时,y=1,
∴平移后与y轴的交点坐标为(0,1),
故选:C.
11.解:∵△ABC,△A1B1C1都是等腰直角三角形,
∴AC=AB=,A1C1=A1B1=2,
∴A1C1=2AC,
由题意A1C1∥AC,
∴AC是△OA1C1的中位线,
∴OA=OA1,
∵A(3,3),
∴A1(6,6),
∵A1B1=2,A1B1∥x轴,
∴B1(4,6),
故选:B.
12.解:∵∠ABC=90°,BC=12,AB=5,
∴AC==13,
根据题意可得EF是AC的垂直平分线,
∴D是AC的中点,
∴AD=AC=6.5,BD=AC=6.5,
∴△ABD的周长为6.5+6.5+5=18.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.解:∵2<<3,2<<3,
∴﹣3<0,﹣2>0,
∴﹣3<﹣2.
故答案为:<.
14.解:根据题意,得:2m﹣1+(﹣3m+)=0,
解得:m=,
∴正数a=(2×﹣1)2=4,
故答案为:4.
15.解:过D作DE⊥AB于E,
在△ABC中,∠C=90°,AB=5,AC=3,
∴BC===4,
∵AD平分∠BAC,
∴DE=DC,
∵AC BC=AC CD+AB DE,即×3×4=×3CD+×5CD,
解得CD=1.5,
∴BD=4﹣CD=4﹣1.5=2.5.
故答案为:2.5.
16.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
17.解:根据题意,AD是∠A的平分线、BC边上的中线也是BC边上的高线,
∴BD=BC=5,∴AD==12.
故应填12.
18.解:∵E为边AD的中点,
∴S△ACD=2S阴影面积=2×10=20,
∵D为边BC的中点,
∴S△ABC=2S△ACD=2×20=40,
故答案为:40.
三.解答题(共7小题,满分66分)
19.解:(1)设y﹣2=kx,
把x=2,y=4代入求得k=1,
∴函数解析式是y=x+2;
(2)∵点M(m,3)在这个函数图象上,
∴3=m+2,
解得:m=1,
∴M(1,3).
20.证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
21.解:(1)如图,△A1B1C1即为所求作.
(2)如图,点P即为所求作.
(3)如图点Q即为所求作.
22.解:( 1 )①∠MON=50°,OE平分∠MON,
∴∠AOB=∠BON=25°,
∵AB∥ON,
∴∠ABO=25°,
故答案为25°;
②当∠BAD=∠ABD时,∠BAD=25°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠AOB+∠ABO+∠OAC+∠BAD=180°,
∴x=∠OAC=180°﹣∠AOB﹣∠ABO﹣∠BAD=180°﹣25°﹣25°﹣25°=105°,
当∠BAD=∠BDA时,
∵∠ABO=25°,
∴∠BAD=77.5°,
∴∠OAB=180°﹣∠ABO﹣∠AOB=180°﹣25°﹣35°=130°,
∴x=∠OAC=∠OAB﹣∠BAD=130°﹣77.5°=52.5°,
故答案为105°;52.5°;
(2)存在这样的∠OAC,使得△ABD中有一个角是另一个角的两倍,其x值分别为20;110;5;125;35;95.
当点D在线段OB上时,
Ⅰ当∠ABD=2∠DAB=90°时,∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=45°﹣25°=20°;
Ⅱ当∠ADB=2∠DAB时,
∵∠ABD=90°,
∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=60°﹣25°=35°;
Ⅲ当∠DAB=2∠ADB时,
∵∠ABD=90°,
∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB﹣∠AOD=30°﹣25°;
当点D在线段OB延长线上时,
Ⅰ当∠ABD=2∠DAB=90°时,∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣45°﹣25°=110°;
Ⅱ当∠ADB=2∠DAB时,
∵∠ABD=90°,
∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣60°﹣25°=95°;
Ⅲ当∠DAB=2∠ADB时,
∵∠ABD=90°,
∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°﹣∠ADB﹣∠AOD=180°﹣30°﹣25°=125°.
综上所述,存在这样的∠OAC,使得△ABD中有一个角是另一个角的两倍.
其x值分别为20;110;5;125;35;95.
23.解:(1)∵∠PAQ=60°,
∴△ACD是等边三角形,
∴AC=AD.∠CAD=60°=∠PAQ,
∴∠PAC=∠QAD,
在△PAC和△QAD中,
,
∴△PAC≌△QAD(SAS),
∴∠ADQ=∠ACB,
∵∠ACB=90°,
∴∠ADQ=90°;
(2)线段CQ与AD的数量关系是:,
位置关系是:CQ∥AD,
∵∠ADQ=90°,∠CQD=90°,
∴∠CQD+∠ADQ=180°,
∴AD∥CQ,
∵△ACD是等边三角形,
∴CD=AD,
∴∠ADC=60°,
∴∠QDC=30°,
∴,
∴.
24.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
25.解:(1)如图4所示:
(2)如图5所示(答案不唯一):
同课章节目录
