2021-2022学年鲁教版八年级上学期数学期末复习综合练习题(前三章)(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级上学期数学期末复习综合练习题(前三章)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 22:51:05 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学第一学期期末复习综合练习题(前三章、附答案)
1.下列由左边到右边的变形中,是因式分解的是( )
A.x2﹣4x+4=(x﹣2)2
B.x2﹣1=x(x﹣)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.(x+2)(x﹣2)=x2﹣4
2.下列各分式中,是最简分式的是( )
A. B. C. D.
3.某班七个学习小组的人数如下:2,3,3,x,4,6,6,已知这组数据的平均数是4,则这个组数据的中位数是( )
A.4 B.4.5 C.5 D.6
4.下列各式:①﹣x2﹣y2=﹣(x+y)(x﹣y),②﹣x2+y2=(﹣x+y)(x+y),③x2﹣2x﹣4=(x﹣2)2,④x2+x+=(x+)2中,分解因式正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.把分式(a、b均不为0且a+b≠0)中的a、b都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.缩小 D.扩大4倍
6.如果x2+2x﹣8=(x+a)(x+b),那么a+b与ab的值分别为 ( )
A.2,8 B.﹣2,8 C.2,﹣8 D.﹣2,﹣8
7.解分式方程=﹣2时,去分母变形正确的是( )
A.﹣1+x=﹣1﹣2(x﹣2) B.1﹣x=1﹣2(x﹣2)
C.﹣1+x=1+2(2﹣x) D.1﹣x=﹣1﹣2(x﹣2)
8.计算(﹣2)2022+(﹣2)2021所得的结果是( )
A.﹣22021 B.﹣1 C.﹣2 D.22021
9.一人自A地步行到B地,速度为a,自B地步行返回到A地,速度为b,这人自A地到B地再返回A地的平均速度为( )
A. B. C. D.
10.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )
A. B.=
C. D.
11.一只船顺流航行90千米与逆流航行60千米所用的时间相等,若水流的速度是2千米/时,求船在静水中的速度.如果设船在静水中的速度为x千米/时,可列出的方程是( )
A.= B.=
C.+3= D.+3=
12.某校对部分参加研学活动的中学生的年龄(单位:岁)进行统计,结果如下表:
年龄 13 14 15 16
人数 1 3 4 2
则这些学生年龄的众数和中位数分别是( )
A.15,15 B.15,13 C.15,14 D.14,15
13.分解因式:﹣2a2+8ab﹣8b2= .
14.当x= 时,分式的值为0.
15.已知样本数据x1,x2,x3,x4的方差为2,则4x1,4x2,4x3,4x4的方差是 .
16.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
17.计算:+的值为 .
18.使分式方程产生增根的n的值为 .
19.先化简,再求值:,其中.
20.2021年是中国共产党成立100年,某商家用10800元购进了一批建党百年纪念衫,上市后果然供不应求,商家又用24000元购进第二批这种纪念衫,所购数量为第一次的2倍,但单价贵了10元.
(1)该商家第一批购买的纪念衫单价是多少元?
(2)若两批纪念衫按相同价格出售,最后剩下50件按标价的8折优惠卖出,如果两批纪念衫全部售完的利润不少于25%(不考虑其他因素),那么每件纪念衫的标价至少是多少元?
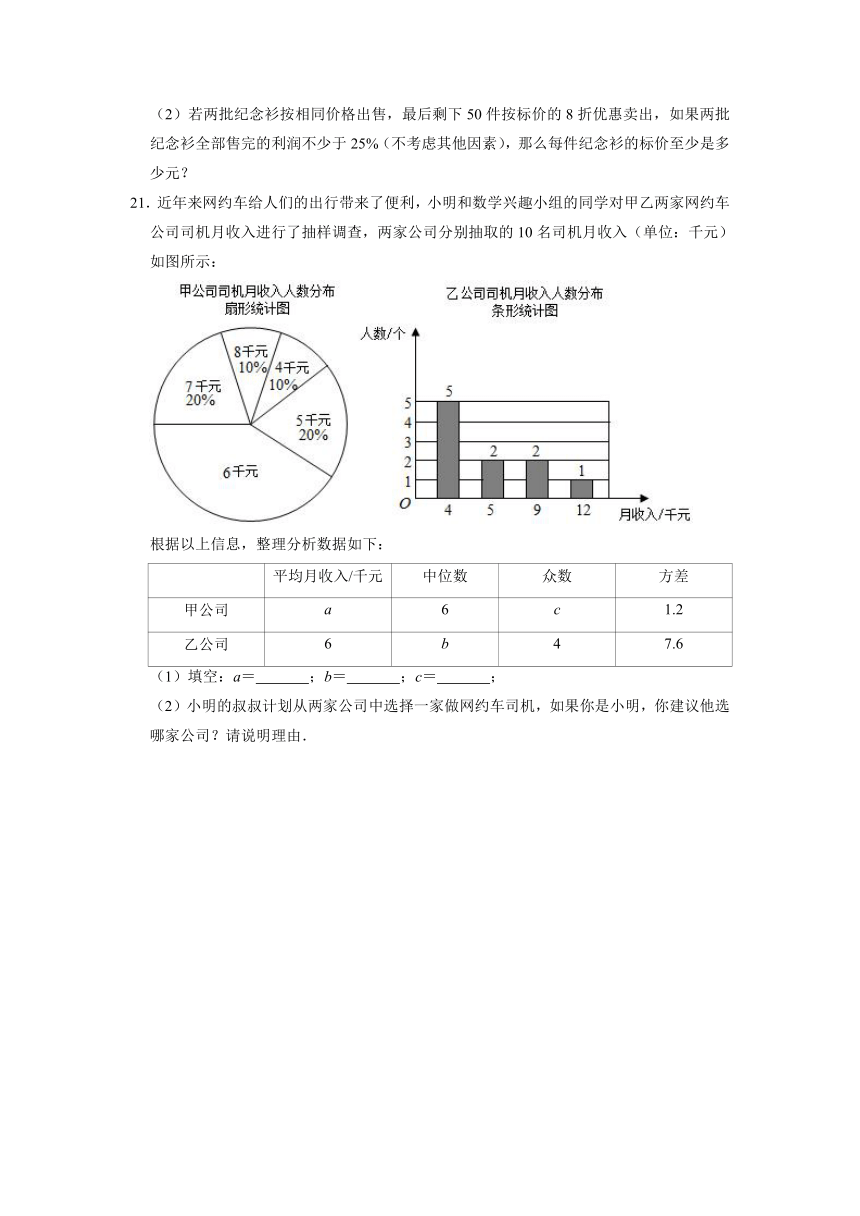
21.近年来网约车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲乙两家网约车公司司机月收入进行了抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数 众数 方差
甲公司 a 6 c 1.2
乙公司 6 b 4 7.6
(1)填空:a= ;b= ;c= ;
(2)小明的叔叔计划从两家公司中选择一家做网约车司机,如果你是小明,你建议他选哪家公司?请说明理由.
参考答案
1.解:A、x2﹣4x+4=(x﹣2)2,是因式分解,故本选项符合题意;
B、x2﹣1=x(x﹣),是分式,所以不是因式分解,故本选项不符合题意;
C、x2﹣4+3x=(x+2)(x﹣2)+3x,等式的右边不是几个整式的积的形式,不是因式分解,故本选项不符合题意;
D、(x+2)(x﹣2)=x2﹣4,是整式乘法,不是因式分解,故本选项不符合题意;
故选:A.
2.解:A.==,不符合题意;
B.==m﹣n,不符合题意;
C.是最简分式,符合题意;
D.==,不符合题意;
故选:C.
3.解:∵2,3,3,x,4,6,6的平均数是4,
∴x=4×7﹣(2+3+3+4+6+6)=4,
∴这组数据为2,3,3,4,4,6,6,
则数据的中位数为4,
故选:A.
4.解:①﹣x2﹣y2=﹣(x2+y2),不符合题意;
②﹣x2+y2=y2﹣x2=(y﹣x)(y+x)=(﹣x+y)(x+y),符合题意;
③(x﹣2)2=x2﹣4x+4,不符合题意;
④x2+x+=x2+2 x +()2=(x+)2,符合题意.
故选:B.
5.解:把分式中的a、b都扩大2倍,
原分式变形为,
∴分式的值扩大2倍,
故选:B.
6.解:已知等式整理得:x2+2x﹣8=x2+(a+b)x+ab,
则a+b=2,ab=﹣8,
故选:C.
7.解:去分母得:1﹣x=﹣1﹣2(x﹣2),
故选:D.
8.解:(﹣2)2022+(﹣2)2021
=(﹣2)2021×(﹣2+1)
=22021.
故选:D.
9.解:设A地到B地路程为“1”,
∴从A到B的时间为:,从B到A的时间为:,
∴平均速度为:==.
故选:B.
10.解:因客户的要求每天的工作效率应该为:(48+x)件,所用的时间为:,
根据“因客户要求提前5天交货”,用原有完成时间减去提前完成时间,
可以列出方程:.
故选:D.
11.解:顺流所用的时间为:;逆流所用的时间为:.所列方程为:=.故选A.
12.解:15出现的次数最多,15是众数.
一共10个学生,按照顺序排列第5、6个学生年龄分别是15、15,
所以中位数为=15.
故选:A.
13.解:原式=﹣2(a2﹣4ab+4b2)
=﹣2(a﹣2b)2.
故答案为:﹣2(a﹣2b)2.
14.解:分式的值为零,
即=0,
也就是x2﹣1=0,
x=±1,
当x=1时,分母等于0,不合题意.
所以当x=﹣1时,分母不等于0,分式的值为零.
故答案为:﹣1.
15.解:样本x1,x2,x3,x4的平均数=(x1+x2+x3+x4),
方差s2=[(x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2]=[(x12+x22+x32+x42)﹣2(x1+x2+x3+x4)+42]=2,
新数据4x1,4x2,4x3,4x4的平均数2=(4x1+4x2+4x3+4x4)=4,
方差s22=[[(4x1﹣4)2+(4x2﹣4)2+(4x3﹣4)2+(4x4﹣4)2]
=[16(x12+x22+x32+x42)+2×16(x1+x2+x3+x4)+4×162]
=16×[(x12+x22+x32+x42)﹣2(x1+x2+x3+x4)+42]
=16×2
=32.
故答案为:32.
16.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
17.解:
=
=
=,
故答案为.
18.解:方程两边都乘x﹣3,得
2﹣x﹣n=7(x﹣3)
∵最简公分母为x﹣3,
∴原方程增根为x=3,
∴把x=3代入整式方程,得n=﹣1.
故答案为:﹣1
19.解:原式=
=
=2m+6.
当时,原式=2×(﹣)+6=5.
20.解:(1)设该商家第一批购买的纪念衫单价是x元,则第二批购买的纪念衫单价是(x+10)元,
依题意得:=2×,
解得:x=90,
经检验,x=90是原方程的解,且符合题意.
答:该商家第一批购买的纪念衫单价是90元.
(2)第一批购买的纪念衫的数量为10800÷90=120(件),
第二批购买的纪念衫的数量为120×2=240(件).
设每件纪念衫的标价是y元,
依题意得:(120+240﹣50)y+50×0.8y≥(10800+24000)×(1+25%),
解得:y≥.
答:每件纪念衫的标价至少是元.
21.解:(1)∵“6千元”对应的百分比为1﹣(10%+20%+10%+20%)=40%,
∴a=4×10%+5×20%+6×40%+7×20%+8×10%=6,c=6,
b==4.5,
故答案为:6、4.5、6;
(2)选甲公司,理由如下:
因为平均数一样,中位数、众数甲公司大于乙公司,且甲公司方差小,更稳定.
1.下列由左边到右边的变形中,是因式分解的是( )
A.x2﹣4x+4=(x﹣2)2
B.x2﹣1=x(x﹣)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.(x+2)(x﹣2)=x2﹣4
2.下列各分式中,是最简分式的是( )
A. B. C. D.
3.某班七个学习小组的人数如下:2,3,3,x,4,6,6,已知这组数据的平均数是4,则这个组数据的中位数是( )
A.4 B.4.5 C.5 D.6
4.下列各式:①﹣x2﹣y2=﹣(x+y)(x﹣y),②﹣x2+y2=(﹣x+y)(x+y),③x2﹣2x﹣4=(x﹣2)2,④x2+x+=(x+)2中,分解因式正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.把分式(a、b均不为0且a+b≠0)中的a、b都扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.缩小 D.扩大4倍
6.如果x2+2x﹣8=(x+a)(x+b),那么a+b与ab的值分别为 ( )
A.2,8 B.﹣2,8 C.2,﹣8 D.﹣2,﹣8
7.解分式方程=﹣2时,去分母变形正确的是( )
A.﹣1+x=﹣1﹣2(x﹣2) B.1﹣x=1﹣2(x﹣2)
C.﹣1+x=1+2(2﹣x) D.1﹣x=﹣1﹣2(x﹣2)
8.计算(﹣2)2022+(﹣2)2021所得的结果是( )
A.﹣22021 B.﹣1 C.﹣2 D.22021
9.一人自A地步行到B地,速度为a,自B地步行返回到A地,速度为b,这人自A地到B地再返回A地的平均速度为( )
A. B. C. D.
10.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )
A. B.=
C. D.
11.一只船顺流航行90千米与逆流航行60千米所用的时间相等,若水流的速度是2千米/时,求船在静水中的速度.如果设船在静水中的速度为x千米/时,可列出的方程是( )
A.= B.=
C.+3= D.+3=
12.某校对部分参加研学活动的中学生的年龄(单位:岁)进行统计,结果如下表:
年龄 13 14 15 16
人数 1 3 4 2
则这些学生年龄的众数和中位数分别是( )
A.15,15 B.15,13 C.15,14 D.14,15
13.分解因式:﹣2a2+8ab﹣8b2= .
14.当x= 时,分式的值为0.
15.已知样本数据x1,x2,x3,x4的方差为2,则4x1,4x2,4x3,4x4的方差是 .
16.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
17.计算:+的值为 .
18.使分式方程产生增根的n的值为 .
19.先化简,再求值:,其中.
20.2021年是中国共产党成立100年,某商家用10800元购进了一批建党百年纪念衫,上市后果然供不应求,商家又用24000元购进第二批这种纪念衫,所购数量为第一次的2倍,但单价贵了10元.
(1)该商家第一批购买的纪念衫单价是多少元?
(2)若两批纪念衫按相同价格出售,最后剩下50件按标价的8折优惠卖出,如果两批纪念衫全部售完的利润不少于25%(不考虑其他因素),那么每件纪念衫的标价至少是多少元?
21.近年来网约车给人们的出行带来了便利,小明和数学兴趣小组的同学对甲乙两家网约车公司司机月收入进行了抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元 中位数 众数 方差
甲公司 a 6 c 1.2
乙公司 6 b 4 7.6
(1)填空:a= ;b= ;c= ;
(2)小明的叔叔计划从两家公司中选择一家做网约车司机,如果你是小明,你建议他选哪家公司?请说明理由.
参考答案
1.解:A、x2﹣4x+4=(x﹣2)2,是因式分解,故本选项符合题意;
B、x2﹣1=x(x﹣),是分式,所以不是因式分解,故本选项不符合题意;
C、x2﹣4+3x=(x+2)(x﹣2)+3x,等式的右边不是几个整式的积的形式,不是因式分解,故本选项不符合题意;
D、(x+2)(x﹣2)=x2﹣4,是整式乘法,不是因式分解,故本选项不符合题意;
故选:A.
2.解:A.==,不符合题意;
B.==m﹣n,不符合题意;
C.是最简分式,符合题意;
D.==,不符合题意;
故选:C.
3.解:∵2,3,3,x,4,6,6的平均数是4,
∴x=4×7﹣(2+3+3+4+6+6)=4,
∴这组数据为2,3,3,4,4,6,6,
则数据的中位数为4,
故选:A.
4.解:①﹣x2﹣y2=﹣(x2+y2),不符合题意;
②﹣x2+y2=y2﹣x2=(y﹣x)(y+x)=(﹣x+y)(x+y),符合题意;
③(x﹣2)2=x2﹣4x+4,不符合题意;
④x2+x+=x2+2 x +()2=(x+)2,符合题意.
故选:B.
5.解:把分式中的a、b都扩大2倍,
原分式变形为,
∴分式的值扩大2倍,
故选:B.
6.解:已知等式整理得:x2+2x﹣8=x2+(a+b)x+ab,
则a+b=2,ab=﹣8,
故选:C.
7.解:去分母得:1﹣x=﹣1﹣2(x﹣2),
故选:D.
8.解:(﹣2)2022+(﹣2)2021
=(﹣2)2021×(﹣2+1)
=22021.
故选:D.
9.解:设A地到B地路程为“1”,
∴从A到B的时间为:,从B到A的时间为:,
∴平均速度为:==.
故选:B.
10.解:因客户的要求每天的工作效率应该为:(48+x)件,所用的时间为:,
根据“因客户要求提前5天交货”,用原有完成时间减去提前完成时间,
可以列出方程:.
故选:D.
11.解:顺流所用的时间为:;逆流所用的时间为:.所列方程为:=.故选A.
12.解:15出现的次数最多,15是众数.
一共10个学生,按照顺序排列第5、6个学生年龄分别是15、15,
所以中位数为=15.
故选:A.
13.解:原式=﹣2(a2﹣4ab+4b2)
=﹣2(a﹣2b)2.
故答案为:﹣2(a﹣2b)2.
14.解:分式的值为零,
即=0,
也就是x2﹣1=0,
x=±1,
当x=1时,分母等于0,不合题意.
所以当x=﹣1时,分母不等于0,分式的值为零.
故答案为:﹣1.
15.解:样本x1,x2,x3,x4的平均数=(x1+x2+x3+x4),
方差s2=[(x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2]=[(x12+x22+x32+x42)﹣2(x1+x2+x3+x4)+42]=2,
新数据4x1,4x2,4x3,4x4的平均数2=(4x1+4x2+4x3+4x4)=4,
方差s22=[[(4x1﹣4)2+(4x2﹣4)2+(4x3﹣4)2+(4x4﹣4)2]
=[16(x12+x22+x32+x42)+2×16(x1+x2+x3+x4)+4×162]
=16×[(x12+x22+x32+x42)﹣2(x1+x2+x3+x4)+42]
=16×2
=32.
故答案为:32.
16.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
17.解:
=
=
=,
故答案为.
18.解:方程两边都乘x﹣3,得
2﹣x﹣n=7(x﹣3)
∵最简公分母为x﹣3,
∴原方程增根为x=3,
∴把x=3代入整式方程,得n=﹣1.
故答案为:﹣1
19.解:原式=
=
=2m+6.
当时,原式=2×(﹣)+6=5.
20.解:(1)设该商家第一批购买的纪念衫单价是x元,则第二批购买的纪念衫单价是(x+10)元,
依题意得:=2×,
解得:x=90,
经检验,x=90是原方程的解,且符合题意.
答:该商家第一批购买的纪念衫单价是90元.
(2)第一批购买的纪念衫的数量为10800÷90=120(件),
第二批购买的纪念衫的数量为120×2=240(件).
设每件纪念衫的标价是y元,
依题意得:(120+240﹣50)y+50×0.8y≥(10800+24000)×(1+25%),
解得:y≥.
答:每件纪念衫的标价至少是元.
21.解:(1)∵“6千元”对应的百分比为1﹣(10%+20%+10%+20%)=40%,
∴a=4×10%+5×20%+6×40%+7×20%+8×10%=6,c=6,
b==4.5,
故答案为:6、4.5、6;
(2)选甲公司,理由如下:
因为平均数一样,中位数、众数甲公司大于乙公司,且甲公司方差小,更稳定.
同课章节目录
