11.2 三角形全等的条件1
文档属性
| 名称 | 11.2 三角形全等的条件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 00:00:00 | ||
图片预览






文档简介
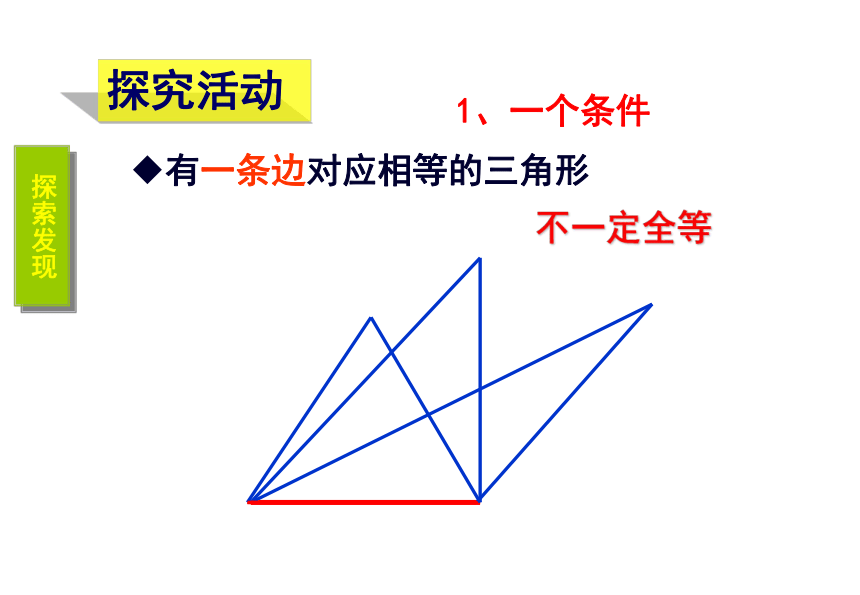
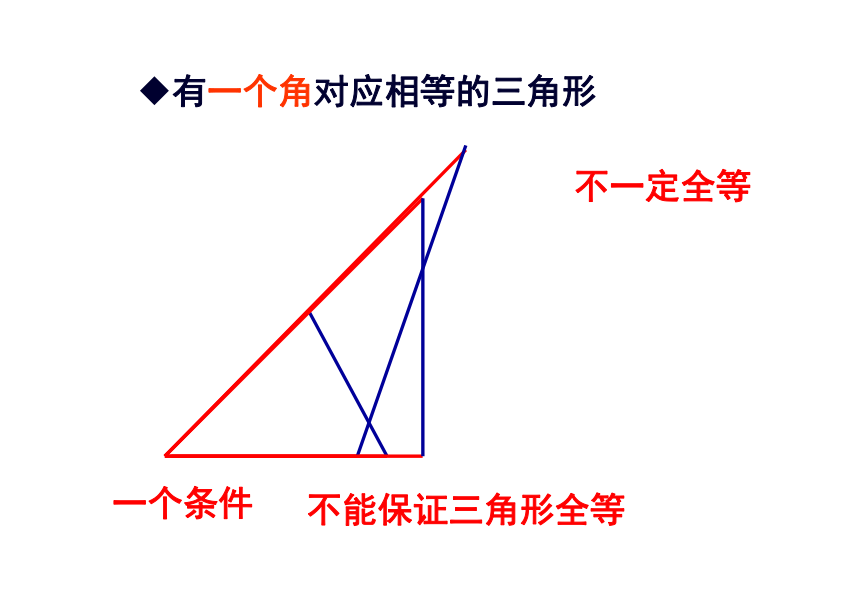
课件24张PPT。11.2 三角形全等的条件(1)复习引入1.下面的两个三角形,请同学们判断这两个三角形是否全 等?探索三角形全等的条件 三边对应相等,三角对应相等的两个三角形全等完全重合的两个三角形全等情境问题: 小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?按照三角形“边、角” 元素进行分类 1、一个条件有一条边对应相等的三角形不一定全等探究活动探索发现有一个角对应相等的三角形不一定全等 一个条件不能保证三角形全等2.给出两个条件:①6cm一边; 30°一内角:② 30°和50°的两内角:③2cm和4cm的两边:有两个条件对应相等不能
保证三角形全等 ①三个角:给出三个条件300700800300700800如30 ,70 ,80, 它们
一定全等吗?结论:三个角对应相等的两个三角形不一定全等.探究二你会用刻度尺和圆规画△ DEF吗?
使其三边分别为3cm,4cm和5cm。把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?1、画线段EF= 3cm。2、分别以E、F为圆心, 5cm , 4cm
长为半径画两条圆弧,交于点D。3、连结DE,DF。△ DEF就是所求的三角形画法:边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S —— 边AB=EFAC=EG(SSS)规范书写:BC=FG在△ABC和△EFG中 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)例题2 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD
如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D.动 态 演 示思考:图1已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?思考:问:
动 态 演 示变式1练习:1.已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC应用拓展聪明题 你会吗已知如图四边形ABCD是平行四边形,
求证: ∠A= ∠C。A C D B?练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?已知:∠AOB
求作:∠DOE, 使∠DOE= ∠AOBAOB练一练:
已知如图,AB=AC,DB=DC,说明∠B =∠C成立的理由ABCD在△ABD和△ACD中,AB=AC (已知)DB=DC (已知) AD=AD (公共边)∴△ABD≌△ACD (SSS)解:连接AD∴ ∠B =∠C(全等三角形的对应角相等)你会用转化思想吗? 经过本节课的学习,你有哪些收获?小结△ABC≌ ( ) △DCBBCCBBF=CD或BD=CFSSS练一练
保证三角形全等 ①三个角:给出三个条件300700800300700800如30 ,70 ,80, 它们
一定全等吗?结论:三个角对应相等的两个三角形不一定全等.探究二你会用刻度尺和圆规画△ DEF吗?
使其三边分别为3cm,4cm和5cm。把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?1、画线段EF= 3cm。2、分别以E、F为圆心, 5cm , 4cm
长为半径画两条圆弧,交于点D。3、连结DE,DF。△ DEF就是所求的三角形画法:边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S —— 边AB=EFAC=EG(SSS)规范书写:BC=FG在△ABC和△EFG中 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)例题2 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD
如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D.动 态 演 示思考:图1已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?思考:问:
动 态 演 示变式1练习:1.已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC应用拓展聪明题 你会吗已知如图四边形ABCD是平行四边形,
求证: ∠A= ∠C。A C D B?练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?已知:∠AOB
求作:∠DOE, 使∠DOE= ∠AOBAOB练一练:
已知如图,AB=AC,DB=DC,说明∠B =∠C成立的理由ABCD在△ABD和△ACD中,AB=AC (已知)DB=DC (已知) AD=AD (公共边)∴△ABD≌△ACD (SSS)解:连接AD∴ ∠B =∠C(全等三角形的对应角相等)你会用转化思想吗? 经过本节课的学习,你有哪些收获?小结△ABC≌ ( ) △DCBBCCBBF=CD或BD=CFSSS练一练
