11.2.2 三角形全等的判定(2)
文档属性
| 名称 | 11.2.2 三角形全等的判定(2) |  | |
| 格式 | zip | ||
| 文件大小 | 145.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 21:13:27 | ||
图片预览



文档简介
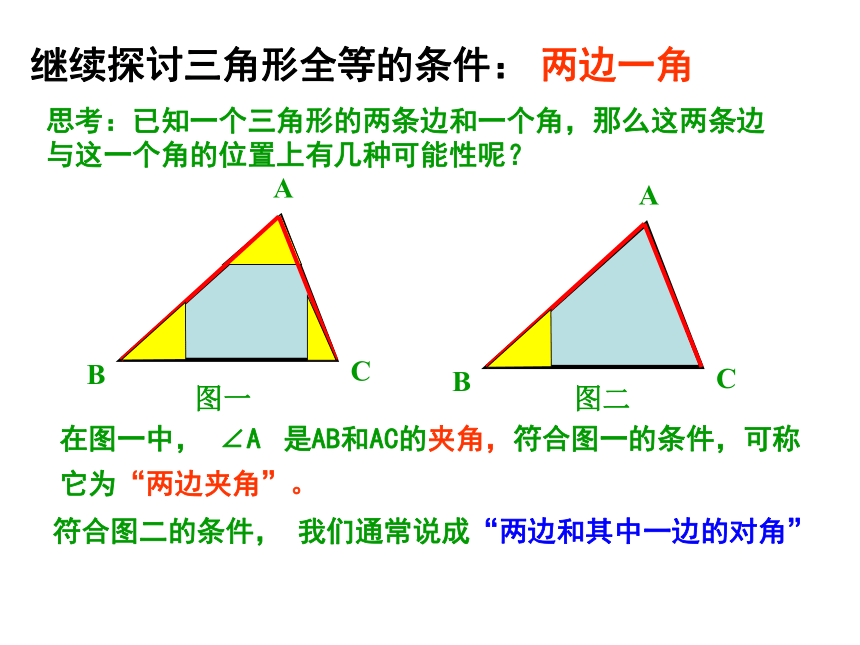
课件17张PPT。§11.2 三角形全等的判定(二)除了SSS外,还有其他情况吗?今天我们继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有四种情况:SSS不能!?继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,符合图一的条件,可称符合图二的条件, 我们通常说成“两边和其中一边的对角”它为“两边夹角”。
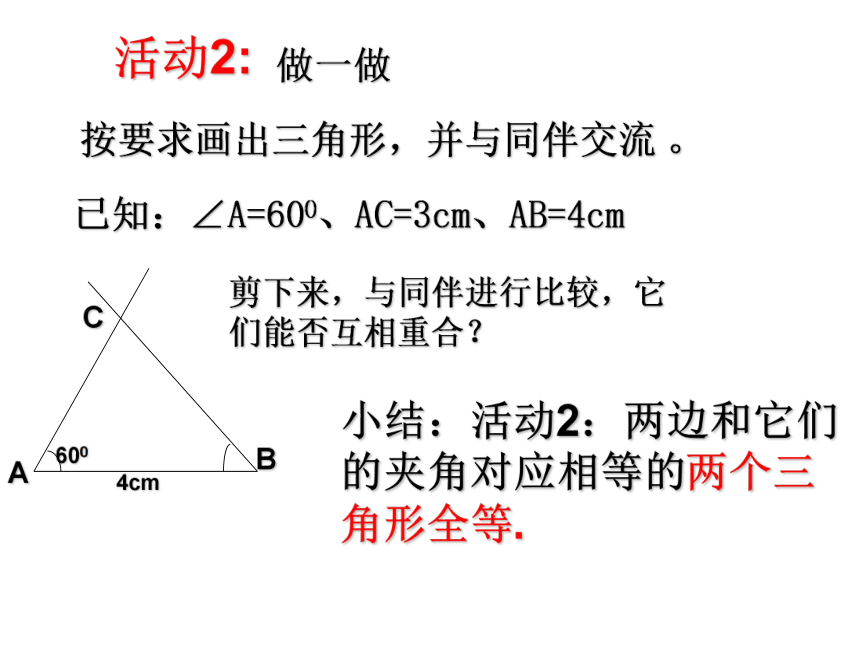
已知:∠A=600、AC=3cm、AB=4cm小结:活动2:两边和它们的夹角对应相等的两个三角形全等.剪下来,与同伴进行比较,它们能否互相重合?活动2:
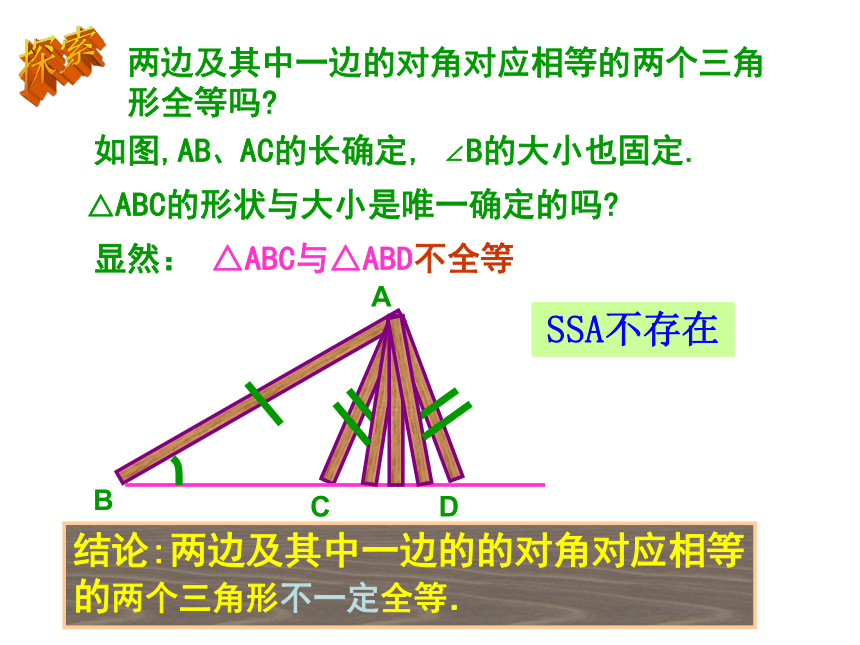
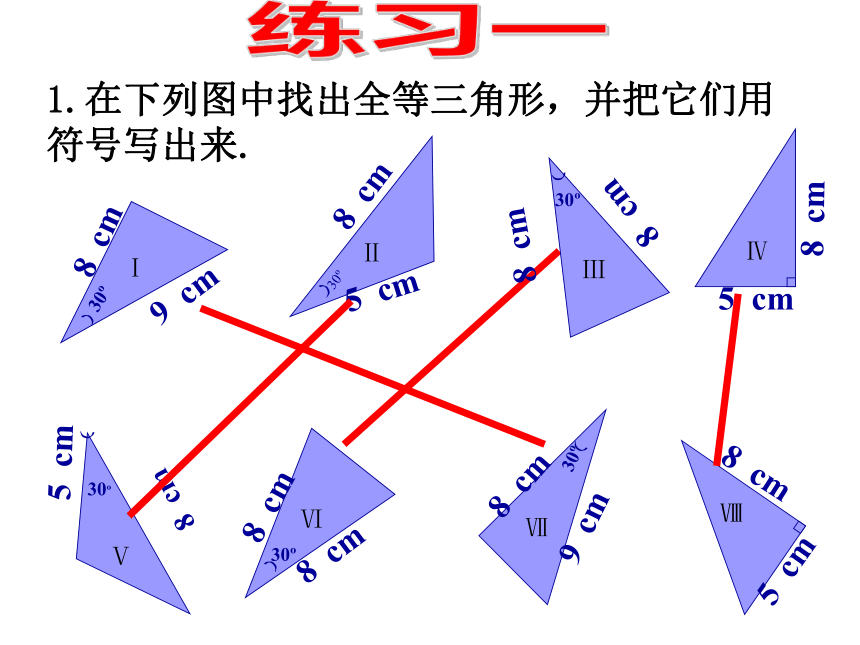
做一做按要求画出三角形,并与同伴交流 。两边及其中一边的对角对应相等的两个三角形全等吗?探索ABC如图,AB、AC的长确定, ∠B的大小也固定.△ABC的形状与大小是唯一确定的吗?D显然: △ABC与△ABD不全等结论:两边及其中一边的的对角对应相等的两个三角形不一定全等.SSA不存在1.在下列图中找出全等三角形,并把它们用
符号写出来.练习一如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?想一想例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?例3.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA S练习二AD=ADBD=CDS3.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●练习三
如图,AC=BD,∠CAB= ∠DBA,
你能判断BC=AD吗?说明理由。说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等1.课本第10页练习1.2
2.课本第15页习题3.4.9.10.13
3.作业本(2)
作业
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,符合图一的条件,可称符合图二的条件, 我们通常说成“两边和其中一边的对角”它为“两边夹角”。
已知:∠A=600、AC=3cm、AB=4cm小结:活动2:两边和它们的夹角对应相等的两个三角形全等.剪下来,与同伴进行比较,它们能否互相重合?活动2:
做一做按要求画出三角形,并与同伴交流 。两边及其中一边的对角对应相等的两个三角形全等吗?探索ABC如图,AB、AC的长确定, ∠B的大小也固定.△ABC的形状与大小是唯一确定的吗?D显然: △ABC与△ABD不全等结论:两边及其中一边的的对角对应相等的两个三角形不一定全等.SSA不存在1.在下列图中找出全等三角形,并把它们用
符号写出来.练习一如图,修补一块玻璃,问取哪一块玻璃可以使得这块新玻璃与原来的完全一样?想一想例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?例3.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA S练习二AD=ADBD=CDS3.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●练习三
如图,AC=BD,∠CAB= ∠DBA,
你能判断BC=AD吗?说明理由。说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等1.课本第10页练习1.2
2.课本第15页习题3.4.9.10.13
3.作业本(2)
作业
