11.2.4 三角形全等的条件
文档属性
| 名称 | 11.2.4 三角形全等的条件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 21:20:43 | ||
图片预览


文档简介
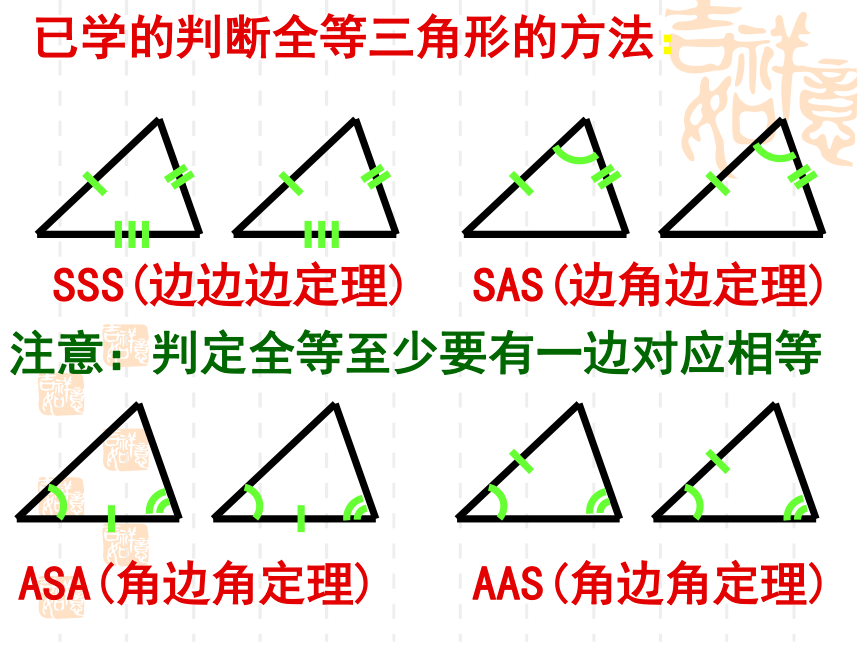
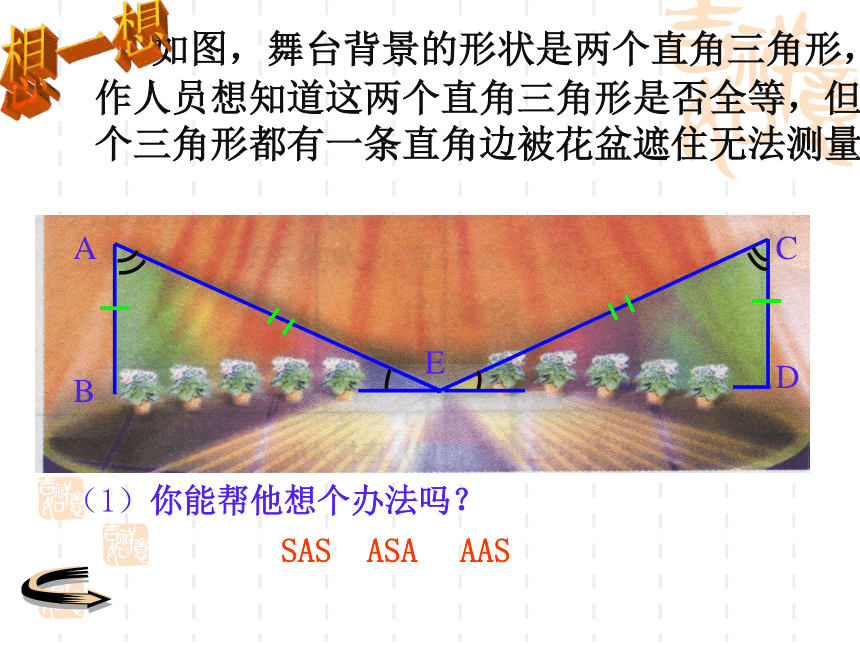
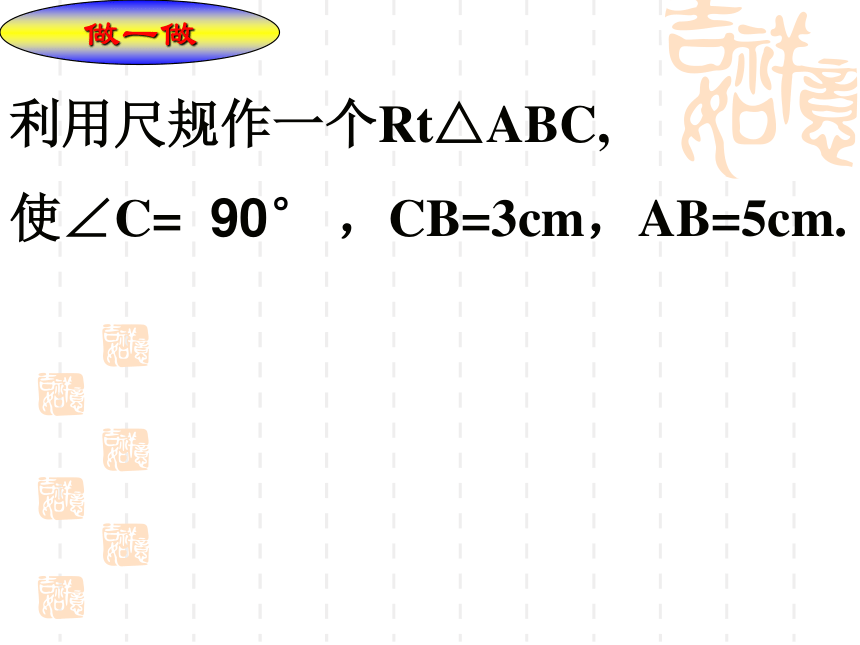
课件13张PPT。直角三角形全等判定已学的判断全等三角形的方法:SSS(边边边定理)SAS(边角边定理)ASA(角边角定理)AAS(角边角定理)注意:判定全等至少要有一边对应相等 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?ABECDSASASAAAS想一想 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(2)如果他只带了一个卷尺,能完成这个任务吗?ABECD 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?想一想做一做利用尺规作一个Rt△ABC,
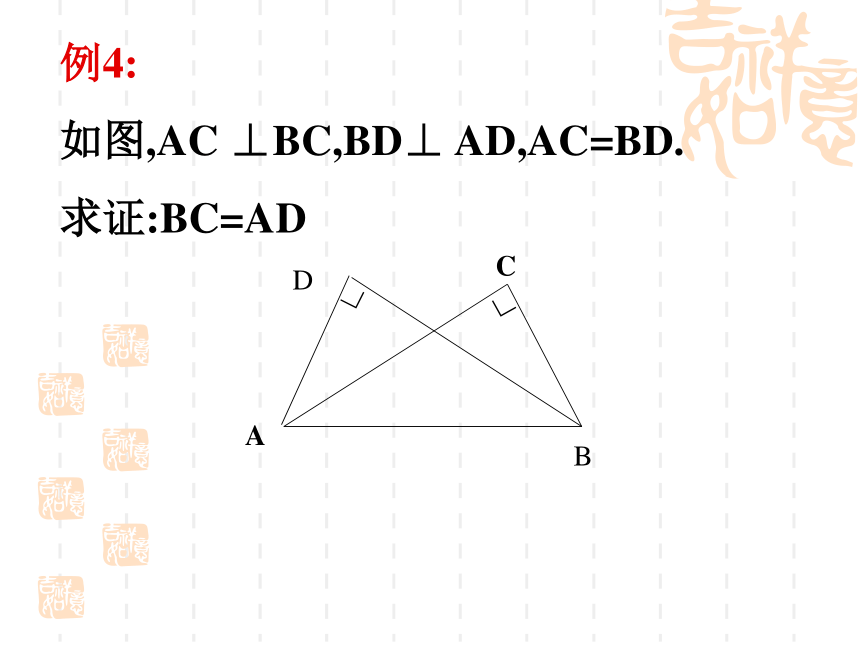
使∠C= 90° ,CB=3cm,AB=5cm.例4:
如图,AC ⊥BC,BD⊥ AD,AC=BD.
求证:BC=AD∟∟如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE巩固练习如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EFG变式训练1如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗?C变式训练2巩固练习P14 1.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?解:DA=EB
理由:∵C为AB中点
∴AC=BC,且CD=CE
又∵ DA⊥AB, EB⊥AB
∴ ∠CAD=∠CBE=90 °
∴在Rt △ACD和Rt △BCE中
CD=CE
AC=BC
∴ Rt △ACD ≌ Rt △BCE
∴ DA=EB
巩固练习P14 2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.证明: ∵ CE=BF
∴ CE-EF=BF-EF 即CF=BE
又∵ AE⊥BC, DF⊥BC
∴ ∠CFD=∠BEA=90 °
∴在Rt △CFD和Rt △BEA中
CD=AB
CF=BE
∴ Rt △CFD≌ Rt △BEA
∴ AE=DF
1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习证明:∵ AB ⊥ BC, AD⊥DC
∴ ∠ABC=∠ADC=90 °
∴在Rt △ABC和Rt △ADC中
AB=AD
AC=AC
∴ Rt △ ABC ≌ Rt △ ADC
∴ ∠ 1= ∠ 21. 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“H.L”.2. 两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对对应边相等).通过这节课的学习你有何收获?
使∠C= 90° ,CB=3cm,AB=5cm.例4:
如图,AC ⊥BC,BD⊥ AD,AC=BD.
求证:BC=AD∟∟如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE巩固练习如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EFG变式训练1如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗?C变式训练2巩固练习P14 1.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?解:DA=EB
理由:∵C为AB中点
∴AC=BC,且CD=CE
又∵ DA⊥AB, EB⊥AB
∴ ∠CAD=∠CBE=90 °
∴在Rt △ACD和Rt △BCE中
CD=CE
AC=BC
∴ Rt △ACD ≌ Rt △BCE
∴ DA=EB
巩固练习P14 2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.证明: ∵ CE=BF
∴ CE-EF=BF-EF 即CF=BE
又∵ AE⊥BC, DF⊥BC
∴ ∠CFD=∠BEA=90 °
∴在Rt △CFD和Rt △BEA中
CD=AB
CF=BE
∴ Rt △CFD≌ Rt △BEA
∴ AE=DF
1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习证明:∵ AB ⊥ BC, AD⊥DC
∴ ∠ABC=∠ADC=90 °
∴在Rt △ABC和Rt △ADC中
AB=AD
AC=AC
∴ Rt △ ABC ≌ Rt △ ADC
∴ ∠ 1= ∠ 21. 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“H.L”.2. 两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对对应边相等).通过这节课的学习你有何收获?
