11.3.1角平分线的性质
图片预览







文档简介
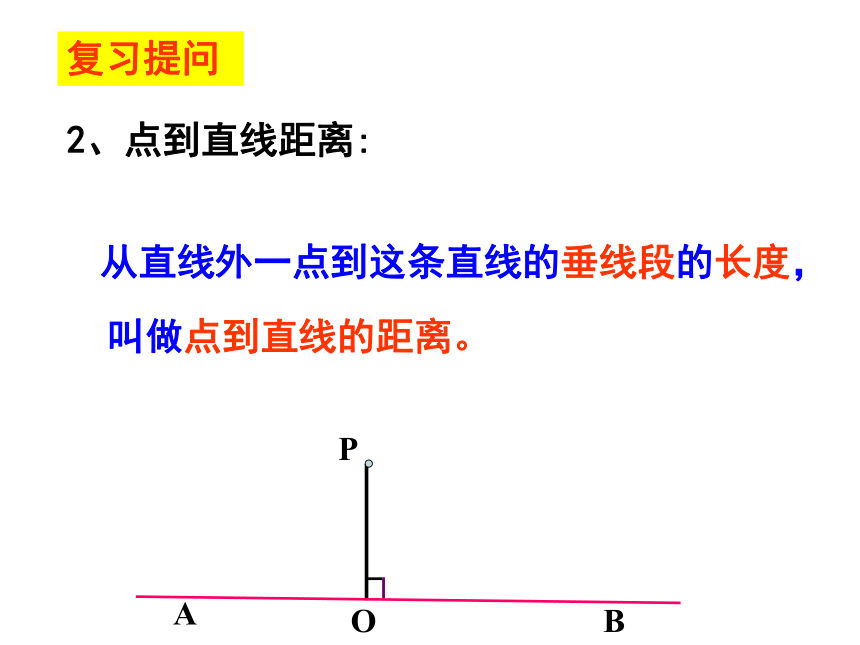
课件23张PPT。13.3角的平分线的性质 第一课时复习提问1、什么叫角平分线?一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。oBCA复习提问 2、点到直线距离:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。 不利用作图工具,请你将一张用纸片做的角分成两个相等的角。
你有什么办法?情景引入探究活动 如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?已知: AOB 求作: AOB的平分线尺规作角的平分线观察领悟作法,探索思考证明方法:ABO画法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.AB为什么OC是角平分线呢? O想一想:已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
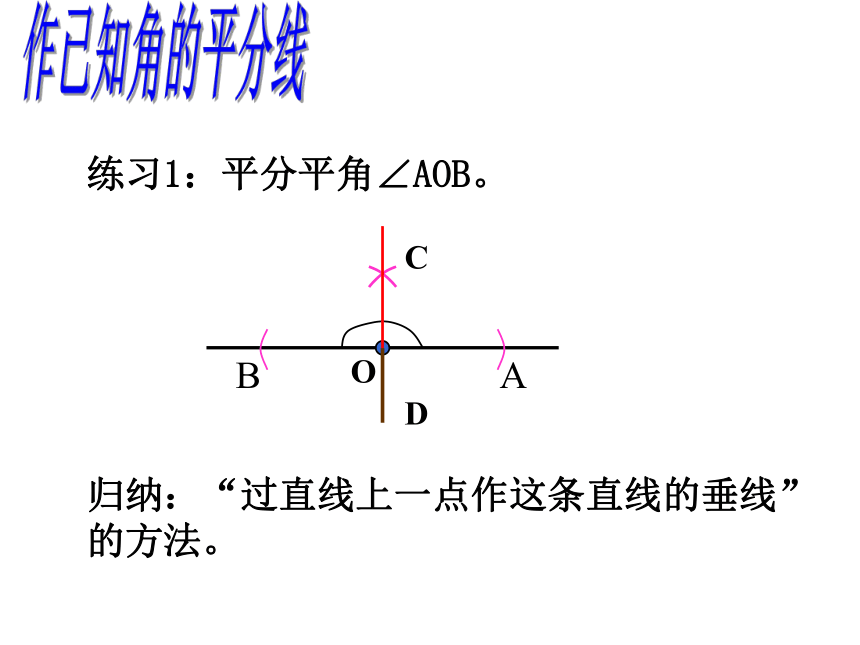
练习1:平分平角∠AOB。
归纳:“过直线上一点作这条直线的垂线”的方法。作已知角的平分线折一折探究角平分线的性质证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。角平分线的性质定理:角的平分线上的点到角的两边的距离相等用符号语言表示为:AOBP12∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)判断:练习∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等
练习如图, ∵ OC是∠AOB的平分线,
又 ________________
∴PD=PE (
)PD⊥OA,PE⊥OB 角的平分线上的点
到角的两边的距离相等例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.ABCMNP怎样找三角形内到三角形三边距离相等的点?练习如图,△ABC的∠B的外角的平分线
BD与∠C的外角的平分线CE相交于点P。
求证:点P到三边AB,BC,CA
所在直线的距离相等。CBAPDE,
练习4 在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.
求BD的长。
如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB巩固提高
◆这节课我们学习了哪些知识? 小 结1、“作已知角的平分线”的尺规作图法;2、角的平分线的性质: 111角的平分线上的点到角的两边的距离相等。
∵ OC是∠AOB的平分线,
又 PD⊥OA,PE⊥OB
∴ PD=PE (角的平分线上的点
到角的两边距离相等). 几何语言:3.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?ABCDE你会吗?
求证:OC平分∠AOB。
练习1:平分平角∠AOB。
归纳:“过直线上一点作这条直线的垂线”的方法。作已知角的平分线折一折探究角平分线的性质证明几何命题的一般步骤:
1、明确命题的已知和求证
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。角平分线的性质定理:角的平分线上的点到角的两边的距离相等用符号语言表示为:AOBP12∵ ∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE
(角的平分线上的点到角的两边的距离相等)
∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)判断:练习∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等
练习如图, ∵ OC是∠AOB的平分线,
又 ________________
∴PD=PE (
)PD⊥OA,PE⊥OB 角的平分线上的点
到角的两边的距离相等例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.ABCMNP怎样找三角形内到三角形三边距离相等的点?练习如图,△ABC的∠B的外角的平分线
BD与∠C的外角的平分线CE相交于点P。
求证:点P到三边AB,BC,CA
所在直线的距离相等。CBAPDE,
练习4 在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.
求BD的长。
如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB巩固提高
◆这节课我们学习了哪些知识? 小 结1、“作已知角的平分线”的尺规作图法;2、角的平分线的性质: 111角的平分线上的点到角的两边的距离相等。
∵ OC是∠AOB的平分线,
又 PD⊥OA,PE⊥OB
∴ PD=PE (角的平分线上的点
到角的两边距离相等). 几何语言:3.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?ABCDE你会吗?
