高中数学人教新课标A版必修2 1.2 空间几何体的三视图和直观图(word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版必修2 1.2 空间几何体的三视图和直观图(word含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 439.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 17:38:07 | ||
图片预览



文档简介
1.2 空间几何体的三视图和直观图
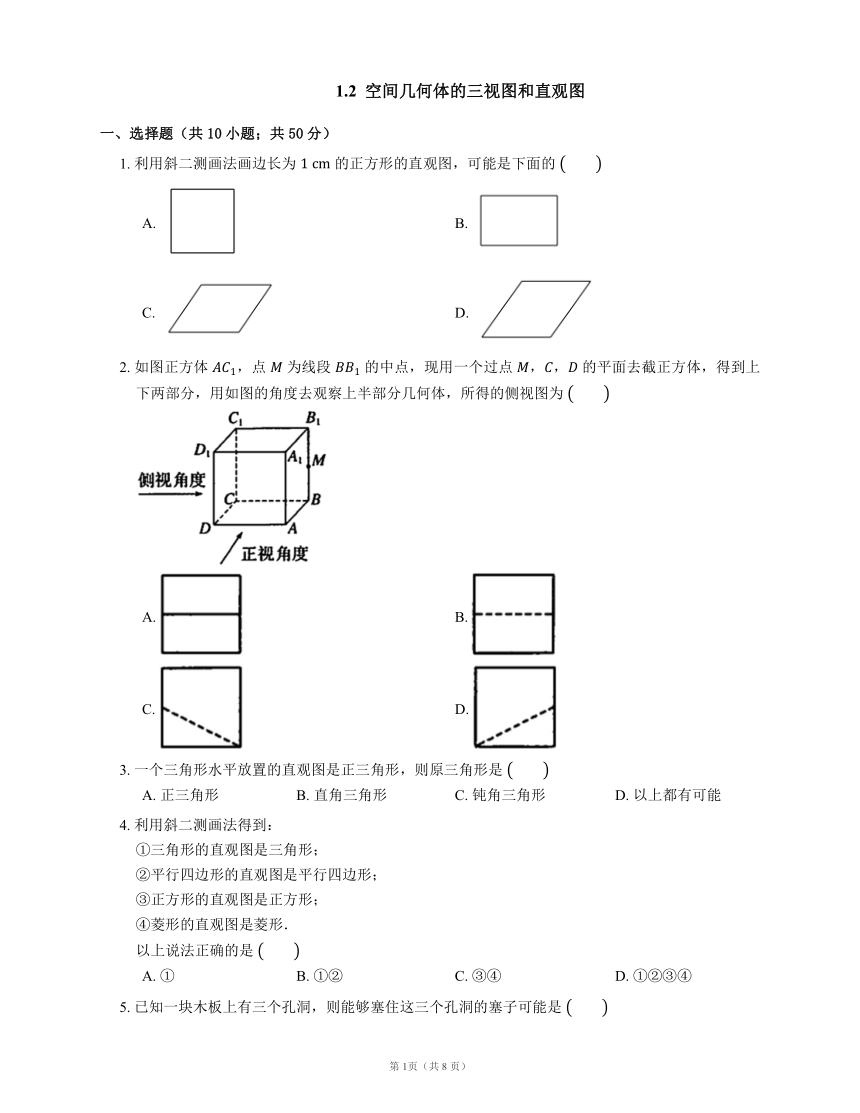
一、选择题(共10小题;共50分)
1. 利用斜二测画法画边长为 的正方形的直观图,可能是下面的
A. B.
C. D.
2. 如图正方体 ,点 为线段 的中点,现用一个过点 ,, 的平面去截正方体,得到上下两部分,用如图的角度去观察上半部分几何体,所得的侧视图为
A. B.
C. D.
3. 一个三角形水平放置的直观图是正三角形,则原三角形是
A. 正三角形 B. 直角三角形 C. 钝角三角形 D. 以上都有可能
4. 利用斜二测画法得到:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上说法正确的是
A. ① B. ①② C. ③④ D. ①②③④
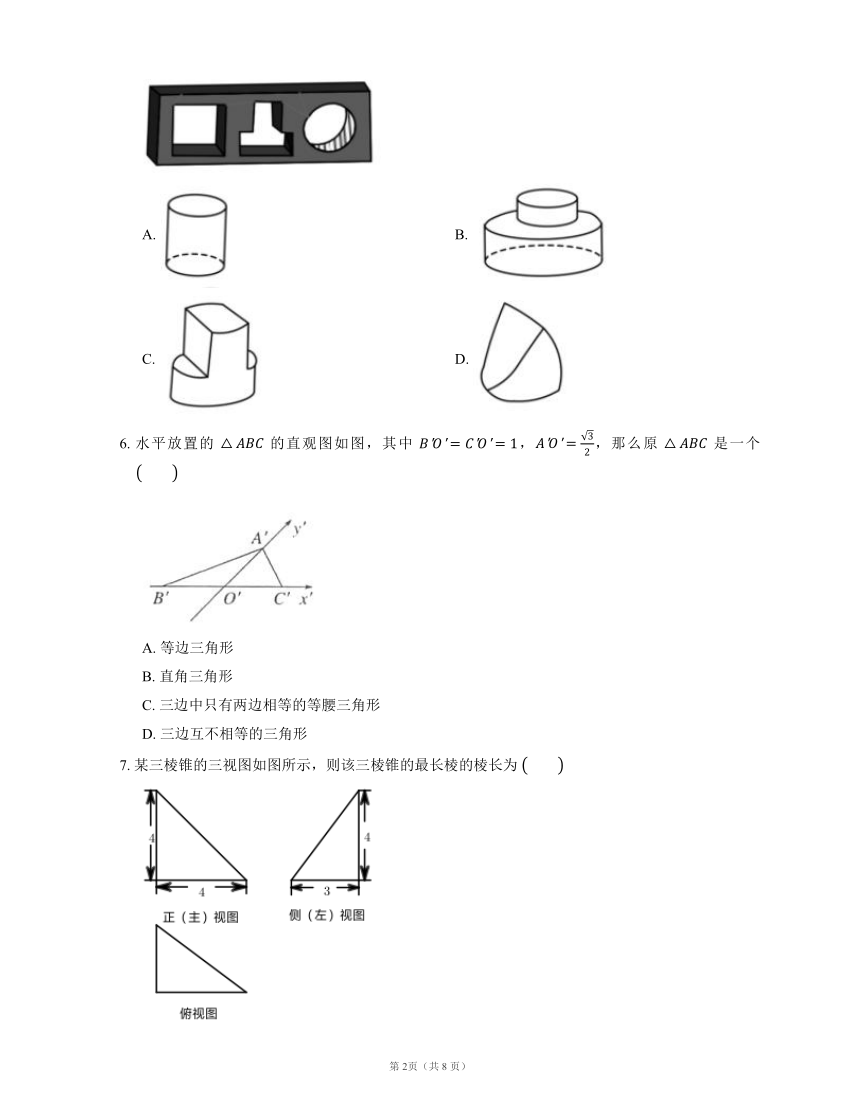
5. 已知一块木板上有三个孔洞,则能够塞住这三个孔洞的塞子可能是
A. B.
C. D.
6. 水平放置的 的直观图如图,其中 ,,那么原 是一个
A. 等边三角形
B. 直角三角形
C. 三边中只有两边相等的等腰三角形
D. 三边互不相等的三角形
7. 某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为
A. B. C. D.
8. 水平放置的 的斜二测直观图如图所示,已知 ,, 轴,则 中 边上的中线的长度为
A. B. C. D.
9. 某几何体的三视图如图所示,则该几何体是
A. 圆柱 B. 圆锥 C. 三棱柱 D. 三棱锥
10. 已知某几何体的三视图如图所示,则该几何体的最长棱为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 直角梯形 ,,,,,,则 水平放置的直观图中 的形状是 .
12. 如图,矩形 是水平放置的一个平面图形的直观图,其中 ,, 轴,则原平面图形的面积为 .
13. 有一个长为 ,宽为 的矩形,则其直观图的面积为 .
14. 若球的主视图的面积为 ,则该球的体积等于 .
15. 四边形 是上底为 ,下底为 ,底角为 的等腰梯形,由斜二测画法,画出这个梯形的直观图为四边形 ,则在直观图中梯形的高为 .
三、解答题(共3小题;共39分)
16. 如图,正方形 的边长为 ,它是水平放置的一个平面图形的直观图.请画出原来的平面图形的形状,并求原图形的周长与面积.
17. 在如图所示的几何体中,圆柱的底面半径 ,高 ,圆锥的高 .试作出这个几何体的三视图.
(提示:以点 为原点, 的方向为 轴的正方向,在前半圆弧 上取点 ,使 ,以 的方向为 轴的正方向, 的方向为 轴的正方向,建立空间直角坐标系.)
18. 用斜二测画法画出六棱锥 的直观图,其中底面 为正六边形,点 在底面上的投影是正六边形的中心 .(尺寸自定)
答案
第一部分
1. C 【解析】正方形的直观图是平行四边形,且边长不相等.
2. B 【解析】上半部分的几何体如图,由此几何体可知,
所得的侧视图为.
3. C
4. C
5. C
【解析】只有C满足与木板上三个孔洞符合:
①侧视为长方形;
②正视为两个长方形拼接;
③从上往下,俯视为圆形;
故与题意相符.
6. A 【解析】由图形知,在原 中,,
为正三角形.
7. C 【解析】根据三视图可还原三棱锥 ,如图所示,
则 ,,,
所以 最长,
故最长棱长为 .
8. A 【解析】由斜二测画法规则知 ,即 为直角三角形,其中 , ,所以 , 边上的中线长度为 .
9. C 【解析】因为主视图和左视图都是长方形,
所以此几何体为柱体,
因为俯视图是一个三角形,
所以此几何体为三棱柱.
10. B
第二部分
11. 等腰三角形
12.
【解析】在直观图中,设 与 轴的交点为 ,则易得 ,所以原平面图形为一边长为 ,高为 的平行四边形,所以其面积为 .
13.
【解析】由于该矩形的面积 ,
所以其直观图的面积 .
14.
【解析】球的主视图为圆,其半径长为 ,即为该球的半径长,因此该球的体积为 .
15.
【解析】按斜二测画法,得梯形的直观图为四边形 ,如图所示,
原图形中梯形的高 ,
在直观图中 ,且 ,
作 垂直于 轴于点 ,则 .
第三部分
16. 如图,建立直角坐标系 ,在 轴上取 ;
在 轴上取 ;
在过点 的 轴的平行线上取
.
连接 ,,, 各点,即得到了原图形.
由作法可知, 为平行四边形,
,
所以 平行四边形 的周长为 ,面积为 .
17.
18. 画法:
()画出六棱锥 的底面.
①在正六边形 中,取 所在的直线为 轴,对称轴 所在的直线为 轴,两轴相交于点 ,如图();画出相应的 轴、 轴、 轴,三轴相交于 ,使 ,,如图();
②在图()中,以 为中点,在 轴上取 ,在 轴上取 ,以点 为中点,画出 平行于 轴,并且长度等于 ,再以 为中点,画出 平行于 轴,并且长度等于 ;
③连接 ,,, 得到正六边形 水平放置的直观图 .
()画出正六棱锥 的顶点,在 轴正半轴上截取点 ,点 异于点 .
()成图.连接 ,,,,,,并擦去 轴、 轴和 轴,便可得到六棱锥 的直观图 ,如图().
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 利用斜二测画法画边长为 的正方形的直观图,可能是下面的
A. B.
C. D.
2. 如图正方体 ,点 为线段 的中点,现用一个过点 ,, 的平面去截正方体,得到上下两部分,用如图的角度去观察上半部分几何体,所得的侧视图为
A. B.
C. D.
3. 一个三角形水平放置的直观图是正三角形,则原三角形是
A. 正三角形 B. 直角三角形 C. 钝角三角形 D. 以上都有可能
4. 利用斜二测画法得到:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上说法正确的是
A. ① B. ①② C. ③④ D. ①②③④
5. 已知一块木板上有三个孔洞,则能够塞住这三个孔洞的塞子可能是
A. B.
C. D.
6. 水平放置的 的直观图如图,其中 ,,那么原 是一个
A. 等边三角形
B. 直角三角形
C. 三边中只有两边相等的等腰三角形
D. 三边互不相等的三角形
7. 某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为
A. B. C. D.
8. 水平放置的 的斜二测直观图如图所示,已知 ,, 轴,则 中 边上的中线的长度为
A. B. C. D.
9. 某几何体的三视图如图所示,则该几何体是
A. 圆柱 B. 圆锥 C. 三棱柱 D. 三棱锥
10. 已知某几何体的三视图如图所示,则该几何体的最长棱为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 直角梯形 ,,,,,,则 水平放置的直观图中 的形状是 .
12. 如图,矩形 是水平放置的一个平面图形的直观图,其中 ,, 轴,则原平面图形的面积为 .
13. 有一个长为 ,宽为 的矩形,则其直观图的面积为 .
14. 若球的主视图的面积为 ,则该球的体积等于 .
15. 四边形 是上底为 ,下底为 ,底角为 的等腰梯形,由斜二测画法,画出这个梯形的直观图为四边形 ,则在直观图中梯形的高为 .
三、解答题(共3小题;共39分)
16. 如图,正方形 的边长为 ,它是水平放置的一个平面图形的直观图.请画出原来的平面图形的形状,并求原图形的周长与面积.
17. 在如图所示的几何体中,圆柱的底面半径 ,高 ,圆锥的高 .试作出这个几何体的三视图.
(提示:以点 为原点, 的方向为 轴的正方向,在前半圆弧 上取点 ,使 ,以 的方向为 轴的正方向, 的方向为 轴的正方向,建立空间直角坐标系.)
18. 用斜二测画法画出六棱锥 的直观图,其中底面 为正六边形,点 在底面上的投影是正六边形的中心 .(尺寸自定)
答案
第一部分
1. C 【解析】正方形的直观图是平行四边形,且边长不相等.
2. B 【解析】上半部分的几何体如图,由此几何体可知,
所得的侧视图为.
3. C
4. C
5. C
【解析】只有C满足与木板上三个孔洞符合:
①侧视为长方形;
②正视为两个长方形拼接;
③从上往下,俯视为圆形;
故与题意相符.
6. A 【解析】由图形知,在原 中,,
为正三角形.
7. C 【解析】根据三视图可还原三棱锥 ,如图所示,
则 ,,,
所以 最长,
故最长棱长为 .
8. A 【解析】由斜二测画法规则知 ,即 为直角三角形,其中 , ,所以 , 边上的中线长度为 .
9. C 【解析】因为主视图和左视图都是长方形,
所以此几何体为柱体,
因为俯视图是一个三角形,
所以此几何体为三棱柱.
10. B
第二部分
11. 等腰三角形
12.
【解析】在直观图中,设 与 轴的交点为 ,则易得 ,所以原平面图形为一边长为 ,高为 的平行四边形,所以其面积为 .
13.
【解析】由于该矩形的面积 ,
所以其直观图的面积 .
14.
【解析】球的主视图为圆,其半径长为 ,即为该球的半径长,因此该球的体积为 .
15.
【解析】按斜二测画法,得梯形的直观图为四边形 ,如图所示,
原图形中梯形的高 ,
在直观图中 ,且 ,
作 垂直于 轴于点 ,则 .
第三部分
16. 如图,建立直角坐标系 ,在 轴上取 ;
在 轴上取 ;
在过点 的 轴的平行线上取
.
连接 ,,, 各点,即得到了原图形.
由作法可知, 为平行四边形,
,
所以 平行四边形 的周长为 ,面积为 .
17.
18. 画法:
()画出六棱锥 的底面.
①在正六边形 中,取 所在的直线为 轴,对称轴 所在的直线为 轴,两轴相交于点 ,如图();画出相应的 轴、 轴、 轴,三轴相交于 ,使 ,,如图();
②在图()中,以 为中点,在 轴上取 ,在 轴上取 ,以点 为中点,画出 平行于 轴,并且长度等于 ,再以 为中点,画出 平行于 轴,并且长度等于 ;
③连接 ,,, 得到正六边形 水平放置的直观图 .
()画出正六棱锥 的顶点,在 轴正半轴上截取点 ,点 异于点 .
()成图.连接 ,,,,,,并擦去 轴、 轴和 轴,便可得到六棱锥 的直观图 ,如图().
第1页(共1 页)
