高中数学人教新课标A版必修2 1.3 空间几何体的表面积与体积 (word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版必修2 1.3 空间几何体的表面积与体积 (word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 201.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 17:41:03 | ||
图片预览


文档简介
1.3 空间几何体的表面积与体积
一、选择题(共10小题;共50分)
1. 一个球的表面积是 ,那么这个球的体积为
A. B. C. D.
2. 已知一个圆柱的底面半径和高分别为 和 ,,侧面展开图是一个长方形,这个长方形的长是宽的 倍,则该圆柱的表面积与侧面积的比是
A. B. C. D.
3. 将表面积为 的圆锥曲线沿母线将其侧面展开,得到一个圆心角为 的扇形,则该圆锥的轴截面的面积为
A. B. C. D.
4. 一个圆锥的侧面积是底面积的 倍,这个圆锥的侧面展开图扇形的圆心角是
A. B. C. D.
5. 一个正四棱台形油槽可以装煤油 ,若它的上、下底边长分别等于 和 ,则它的深度是
A. B. C. D.
6. 已知某圆台的一个底面周长是另一个底面周长的 倍,母线长为 ,圆台的侧面积为 ,则该圆台较小底面的半径为
A. B. C. D.
7. 将若干毫升水倒入底面半径为 的圆柱形器皿中,量得水面的高度为 ,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是
A. B. C. D.
8. 将一个棱长为 的正方体切成 个全等的小正方体,则表面积增加了
A. B. C. D.
9. 是边长为 的等边三角形, 为 的中点.将 沿 折起到 的位置,则当三棱锥 的体积最大时,三棱锥 外接球的表面积为
A. B. C. D.
10. 正三棱柱 的各棱长均为 , 为 的中点,则四面体 的体积是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知圆柱的底面积为 ,轴截面的面积为 ,则它的侧面面积为 .
12. 若正四棱柱的底面的面积为 ,其对角线和底面成 角,则此正四棱柱的全面积是 .
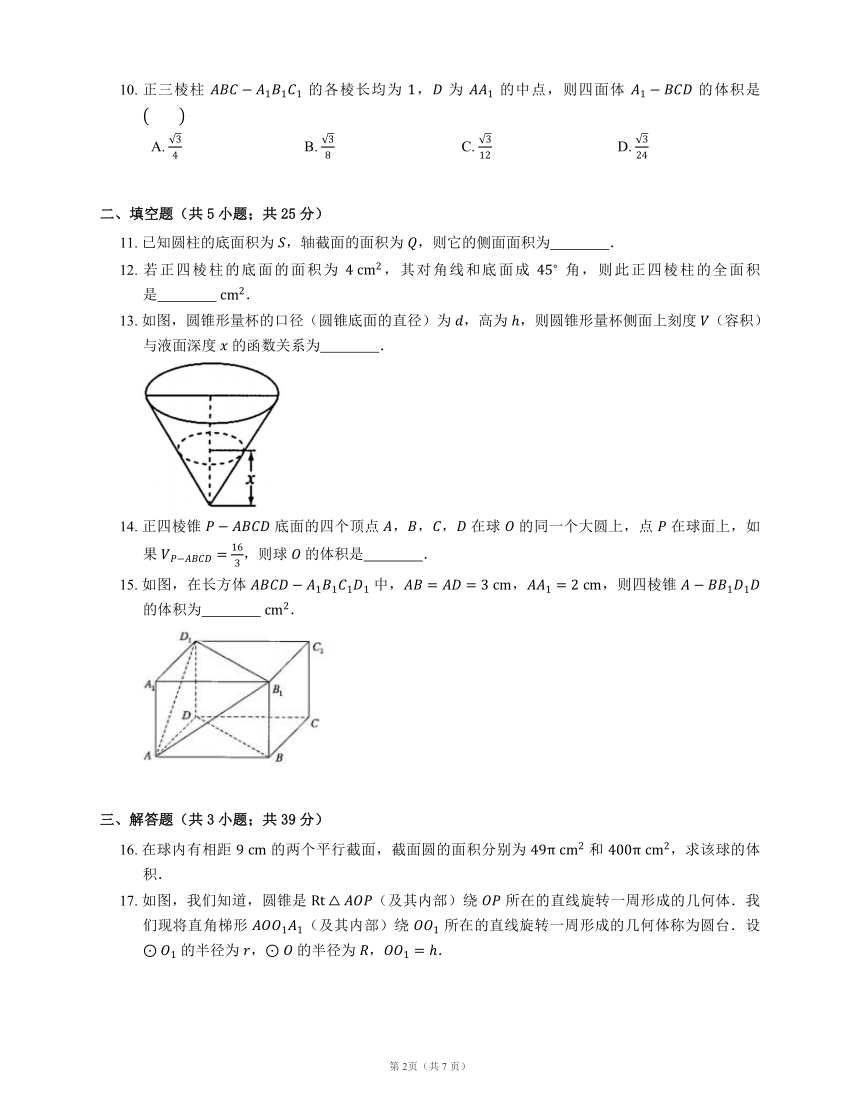
13. 如图,圆锥形量杯的口径(圆锥底面的直径)为 ,高为 ,则圆锥形量杯侧面上刻度 (容积)与液面深度 的函数关系为 .
14. 正四棱锥 底面的四个顶点 ,,, 在球 的同一个大圆上,点 在球面上,如果 ,则球 的体积是 .
15. 如图,在长方体 中,,,则四棱锥 的体积为 .
三、解答题(共3小题;共39分)
16. 在球内有相距 的两个平行截面,截面圆的面积分别为 和 ,求该球的体积.
17. 如图,我们知道,圆锥是 (及其内部)绕 所在的直线旋转一周形成的几何体.我们现将直角梯形 (及其内部)绕 所在的直线旋转一周形成的几何体称为圆台.设 的半径为 , 的半径为 ,.
(1)求证:圆台的体积 ;
(2)若 ,,,求圆台的表面积 .
18. 某人买了一罐容积为 升、高为 米的直三棱柱型罐装进口液体车油,由于不小心摔落地上,结果有两处破损并发生渗漏,它们的位置分别在两条棱上且距下底面的高度分别为 , 的地方(单位:米).且上底面的容器盖也被摔破了,为了减少罐内液体油的损失,该人采用破口朝上,倾斜罐口的方式拿回家.试问罐内的液体车油最理想的情况下估计能剩多少.
答案
第一部分
1. B 【解析】设这个球的半径为 ,
则 ,
得 ,
所以这个球的体积 .
2. A 【解析】由题意可知 ,
所以 ,
则该圆柱的表面积与侧面积的比是 .
3. B
4. D
5. D
【解析】设深度为 ,则 ,
即 ,解得 .
6. A 【解析】设圆台较小底面的半径为 ,则另一底面的半径为 .
由 ,
解得 .
7. B 【解析】设倒圆锥形器皿中水面的高度为 ,水面半径为 ,则母线(含水部分),
所以 ,即 ,
所以 ,
所以 ,
所以 ,
解得 .
8. B 【解析】棱长为 的正方体的表面积为 ,由棱长为 的正方体切成的 个全等的小正方体的表面积和为 ,因此表面积增加了 .
9. C 【解析】当三棱锥 的体积最大时, 点最高,
此时 ,,,
因为三棱锥 的外接球与以 ,, 为邻边的长方体的外接球是同一个球,设其半径为 ,
又因为 ,,
所以 ,
所以三棱锥 外接球的表面积为 .
10. D
【解析】如图,
因为 为正三棱柱,
所以底面 为正三角形,侧面 为正方形,
第二部分
11.
12.
13.
14.
【解析】如图,正四棱锥 底面的四个顶点 ,,, 在球 的同一个大圆上,点 在球面上,
所以 ,,,,
所以 ,
解得 ,
所以球 的体积 .
15.
【解析】过点 作 于点 ,
是四棱锥 的高,
所以 ,
所以四棱锥 的体积为 .
第三部分
16.
17. (1) 因为 ,
所以 ,解得 ,
所以 .
(2) 在 中,过点 作 , 是垂足,
则在 中,,,
所以 ,
所以 ,,
所以该圆台的表面积 .
18. 首先据题意画出示意图(如图①).
直三棱柱为 ,破损处为 ,,并且 ,,
.
其次,“罐内的液体车油最理想的情况下估计能剩多少”翻译为数学语言即“罐内所剩液体车油的最大值为多少 ”
再次,过 , 两点的平面同时应过 ,才能使所剩液体车油达到最大值,故问题转化为求几何体 的体积.
最后,求该不规则几何体的体积,办法不唯一,其中一种如下:
因为 ,而 ,故只需求 (如图②).
由 及 ,
可求得 .
于是,最理想的情况下估计能剩下 升.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 一个球的表面积是 ,那么这个球的体积为
A. B. C. D.
2. 已知一个圆柱的底面半径和高分别为 和 ,,侧面展开图是一个长方形,这个长方形的长是宽的 倍,则该圆柱的表面积与侧面积的比是
A. B. C. D.
3. 将表面积为 的圆锥曲线沿母线将其侧面展开,得到一个圆心角为 的扇形,则该圆锥的轴截面的面积为
A. B. C. D.
4. 一个圆锥的侧面积是底面积的 倍,这个圆锥的侧面展开图扇形的圆心角是
A. B. C. D.
5. 一个正四棱台形油槽可以装煤油 ,若它的上、下底边长分别等于 和 ,则它的深度是
A. B. C. D.
6. 已知某圆台的一个底面周长是另一个底面周长的 倍,母线长为 ,圆台的侧面积为 ,则该圆台较小底面的半径为
A. B. C. D.
7. 将若干毫升水倒入底面半径为 的圆柱形器皿中,量得水面的高度为 ,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是
A. B. C. D.
8. 将一个棱长为 的正方体切成 个全等的小正方体,则表面积增加了
A. B. C. D.
9. 是边长为 的等边三角形, 为 的中点.将 沿 折起到 的位置,则当三棱锥 的体积最大时,三棱锥 外接球的表面积为
A. B. C. D.
10. 正三棱柱 的各棱长均为 , 为 的中点,则四面体 的体积是
A. B. C. D.
二、填空题(共5小题;共25分)
11. 已知圆柱的底面积为 ,轴截面的面积为 ,则它的侧面面积为 .
12. 若正四棱柱的底面的面积为 ,其对角线和底面成 角,则此正四棱柱的全面积是 .
13. 如图,圆锥形量杯的口径(圆锥底面的直径)为 ,高为 ,则圆锥形量杯侧面上刻度 (容积)与液面深度 的函数关系为 .
14. 正四棱锥 底面的四个顶点 ,,, 在球 的同一个大圆上,点 在球面上,如果 ,则球 的体积是 .
15. 如图,在长方体 中,,,则四棱锥 的体积为 .
三、解答题(共3小题;共39分)
16. 在球内有相距 的两个平行截面,截面圆的面积分别为 和 ,求该球的体积.
17. 如图,我们知道,圆锥是 (及其内部)绕 所在的直线旋转一周形成的几何体.我们现将直角梯形 (及其内部)绕 所在的直线旋转一周形成的几何体称为圆台.设 的半径为 , 的半径为 ,.
(1)求证:圆台的体积 ;
(2)若 ,,,求圆台的表面积 .
18. 某人买了一罐容积为 升、高为 米的直三棱柱型罐装进口液体车油,由于不小心摔落地上,结果有两处破损并发生渗漏,它们的位置分别在两条棱上且距下底面的高度分别为 , 的地方(单位:米).且上底面的容器盖也被摔破了,为了减少罐内液体油的损失,该人采用破口朝上,倾斜罐口的方式拿回家.试问罐内的液体车油最理想的情况下估计能剩多少.
答案
第一部分
1. B 【解析】设这个球的半径为 ,
则 ,
得 ,
所以这个球的体积 .
2. A 【解析】由题意可知 ,
所以 ,
则该圆柱的表面积与侧面积的比是 .
3. B
4. D
5. D
【解析】设深度为 ,则 ,
即 ,解得 .
6. A 【解析】设圆台较小底面的半径为 ,则另一底面的半径为 .
由 ,
解得 .
7. B 【解析】设倒圆锥形器皿中水面的高度为 ,水面半径为 ,则母线(含水部分),
所以 ,即 ,
所以 ,
所以 ,
所以 ,
解得 .
8. B 【解析】棱长为 的正方体的表面积为 ,由棱长为 的正方体切成的 个全等的小正方体的表面积和为 ,因此表面积增加了 .
9. C 【解析】当三棱锥 的体积最大时, 点最高,
此时 ,,,
因为三棱锥 的外接球与以 ,, 为邻边的长方体的外接球是同一个球,设其半径为 ,
又因为 ,,
所以 ,
所以三棱锥 外接球的表面积为 .
10. D
【解析】如图,
因为 为正三棱柱,
所以底面 为正三角形,侧面 为正方形,
第二部分
11.
12.
13.
14.
【解析】如图,正四棱锥 底面的四个顶点 ,,, 在球 的同一个大圆上,点 在球面上,
所以 ,,,,
所以 ,
解得 ,
所以球 的体积 .
15.
【解析】过点 作 于点 ,
是四棱锥 的高,
所以 ,
所以四棱锥 的体积为 .
第三部分
16.
17. (1) 因为 ,
所以 ,解得 ,
所以 .
(2) 在 中,过点 作 , 是垂足,
则在 中,,,
所以 ,
所以 ,,
所以该圆台的表面积 .
18. 首先据题意画出示意图(如图①).
直三棱柱为 ,破损处为 ,,并且 ,,
.
其次,“罐内的液体车油最理想的情况下估计能剩多少”翻译为数学语言即“罐内所剩液体车油的最大值为多少 ”
再次,过 , 两点的平面同时应过 ,才能使所剩液体车油达到最大值,故问题转化为求几何体 的体积.
最后,求该不规则几何体的体积,办法不唯一,其中一种如下:
因为 ,而 ,故只需求 (如图②).
由 及 ,
可求得 .
于是,最理想的情况下估计能剩下 升.
第1页(共1 页)
