沪科版数学八年级上册 15.3 等腰三角形性质课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.3 等腰三角形性质课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 08:54:15 | ||
图片预览



文档简介
(共15张PPT)
A
C
B
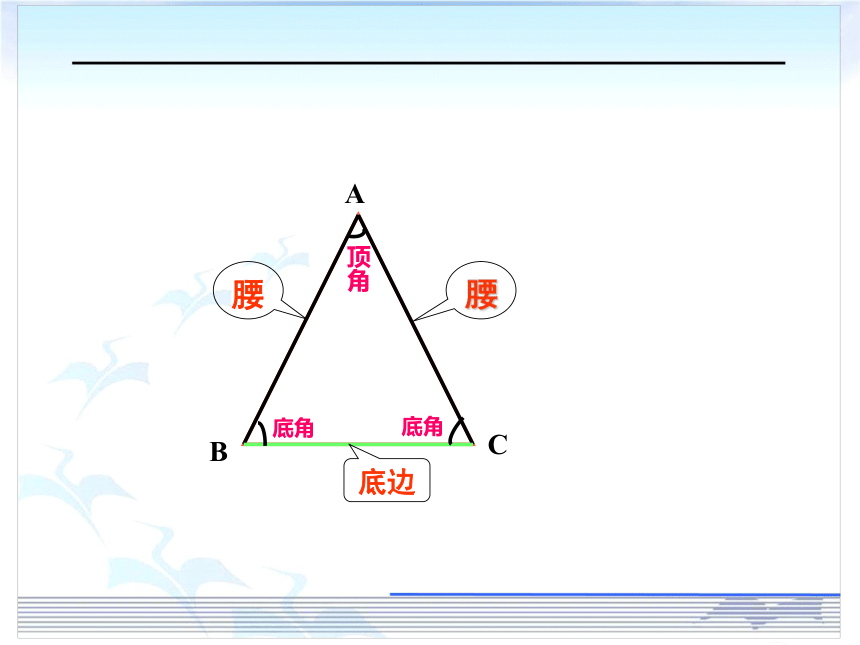
腰
腰
底边
顶角
底角
底角
等腰三角形是轴对称图形,折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形吗?
对称轴是什么?
等腰三角形的两个底角相等.
A
C
B
D
2、如何添加辅助线?有几种添法?
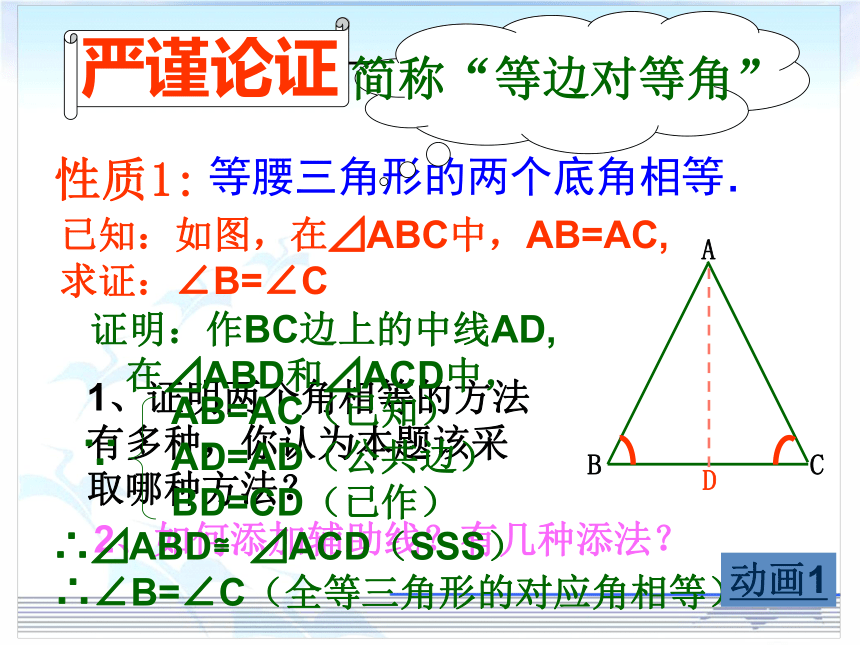
严谨论证
性质1:
简称“等边对等角”
已知:如图,在⊿ABC中,AB=AC,
求证:∠B=∠C
1、证明两个角相等的方法有多种,你认为本题该采取哪种方法?
证明:作BC边上的中线AD,
在⊿ABD和⊿ACD中,
∴⊿ABD≌⊿ACD(SSS)
∴∠B=∠C(全等三角形的对应角相等)
AB=AC(已知)
AD=AD(公共边)
BD=CD(已作)
∵
动画1
归纳结论
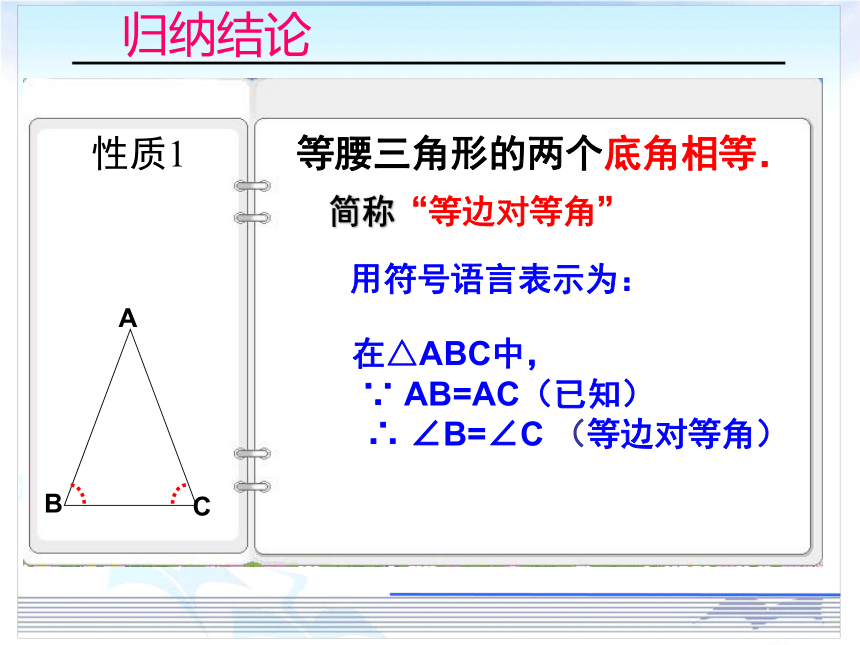
等腰三角形的两个底角相等.
性质1
简称“等边对等角”
用符号语言表示为:
在△ABC中,
∵ AB=AC(已知)
∴ ∠B=∠C (等边对等角)
A
B
C
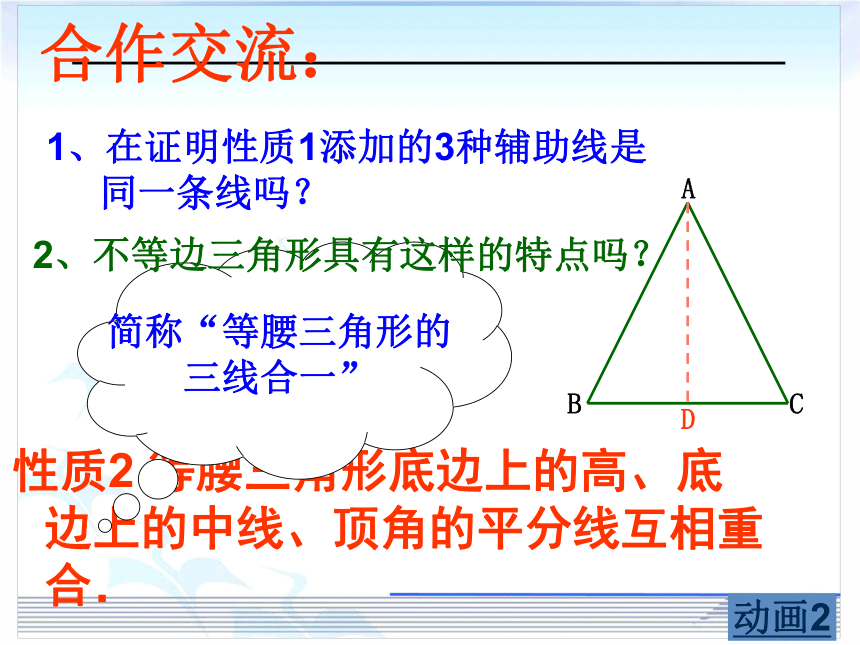
性质2 等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合.
A
C
B
D
简称“等腰三角形的
三线合一”
1、在证明性质1添加的3种辅助线是
同一条线吗?
合作交流:
2、不等边三角形具有这样的特点吗?
动画2
性质2可分解成下面三个方面来理解:
1、等腰三角形顶角的平分线,既是底边上的中线,又是底边上的高.
符号语言:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线.
符号语言:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线.
符号语言:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
A
C
B
D
1
2
思考:等腰三角形的对称轴还可以怎样回答?
等腰三角形是轴对称图形.对称轴是底边上的中线(顶角平分线,底边上的高)所在直线
注意:等边三角形具有等腰三角形所具有的所有性质.
推论:等边三角形的三个内角相等,
每个内角都等于60°.
A
C
B
在△ABC中,AB=AC=BC,它是__________三角形
(1)它是等腰三角形吗?
(2)∠A、∠B、∠C相等吗?为什么?
等边
例1 已知:如图,在⊿ABC中 AB=AC,∠BAC=120°点D、E是底边上两点,且 BD=AD,CE=AE.
求∠DAE的度数。
A
B
C
D
E
例题解析
图中有几个等腰三角形?各个底角是多少度?
解∵AB=AC(已知)
∴∠B=∠C(等边对等角)
又∵BD=AD
∴∠BAD=∠B=30°(等边对等角)
同理∠EAC=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°
例题解析
A
B
C
D
E
动脑筋
70°,70°或40°,100°
70°,70°
3.等腰三角形一个角为40°,它的另外两个角为
.
1、已知等腰三角形的一个底角为40°,它的另外两个角为 .
2、已知等腰三角形的顶角为40°,它的另外两个角为 .
4.等腰三角形一个角为120°,它的另外两个角为 .
40°,100°
30°,30°
小游戏
轴对称图形
性质1:两个底角相等(等边对等角)
性质2:顶角平分线、底边上的中线、
和底边上的高互相重合(三线合 一)
等边三角形的每个角都相等,都等于60°
小结:
。
1、本节课学习了哪些内容?
2、我的感想是 . 。
3、 我存在的疑惑是 .。
小结:
作业:
1、巩固性作业:习题15.3第1,3题.
2、操作性作业: 你能不能利用长方形纸片,剪一个等边三角形.
3、探究性作业:等腰三角形两腰上的中线有什么关系吗?两腰上的高呢?利用类似的方法,还可以得到等腰三角形中哪些线段相等?
A
C
B
腰
腰
底边
顶角
底角
底角
等腰三角形是轴对称图形,折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形吗?
对称轴是什么?
等腰三角形的两个底角相等.
A
C
B
D
2、如何添加辅助线?有几种添法?
严谨论证
性质1:
简称“等边对等角”
已知:如图,在⊿ABC中,AB=AC,
求证:∠B=∠C
1、证明两个角相等的方法有多种,你认为本题该采取哪种方法?
证明:作BC边上的中线AD,
在⊿ABD和⊿ACD中,
∴⊿ABD≌⊿ACD(SSS)
∴∠B=∠C(全等三角形的对应角相等)
AB=AC(已知)
AD=AD(公共边)
BD=CD(已作)
∵
动画1
归纳结论
等腰三角形的两个底角相等.
性质1
简称“等边对等角”
用符号语言表示为:
在△ABC中,
∵ AB=AC(已知)
∴ ∠B=∠C (等边对等角)
A
B
C
性质2 等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合.
A
C
B
D
简称“等腰三角形的
三线合一”
1、在证明性质1添加的3种辅助线是
同一条线吗?
合作交流:
2、不等边三角形具有这样的特点吗?
动画2
性质2可分解成下面三个方面来理解:
1、等腰三角形顶角的平分线,既是底边上的中线,又是底边上的高.
符号语言:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线.
符号语言:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线.
符号语言:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
A
C
B
D
1
2
思考:等腰三角形的对称轴还可以怎样回答?
等腰三角形是轴对称图形.对称轴是底边上的中线(顶角平分线,底边上的高)所在直线
注意:等边三角形具有等腰三角形所具有的所有性质.
推论:等边三角形的三个内角相等,
每个内角都等于60°.
A
C
B
在△ABC中,AB=AC=BC,它是__________三角形
(1)它是等腰三角形吗?
(2)∠A、∠B、∠C相等吗?为什么?
等边
例1 已知:如图,在⊿ABC中 AB=AC,∠BAC=120°点D、E是底边上两点,且 BD=AD,CE=AE.
求∠DAE的度数。
A
B
C
D
E
例题解析
图中有几个等腰三角形?各个底角是多少度?
解∵AB=AC(已知)
∴∠B=∠C(等边对等角)
又∵BD=AD
∴∠BAD=∠B=30°(等边对等角)
同理∠EAC=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°
例题解析
A
B
C
D
E
动脑筋
70°,70°或40°,100°
70°,70°
3.等腰三角形一个角为40°,它的另外两个角为
.
1、已知等腰三角形的一个底角为40°,它的另外两个角为 .
2、已知等腰三角形的顶角为40°,它的另外两个角为 .
4.等腰三角形一个角为120°,它的另外两个角为 .
40°,100°
30°,30°
小游戏
轴对称图形
性质1:两个底角相等(等边对等角)
性质2:顶角平分线、底边上的中线、
和底边上的高互相重合(三线合 一)
等边三角形的每个角都相等,都等于60°
小结:
。
1、本节课学习了哪些内容?
2、我的感想是 . 。
3、 我存在的疑惑是 .。
小结:
作业:
1、巩固性作业:习题15.3第1,3题.
2、操作性作业: 你能不能利用长方形纸片,剪一个等边三角形.
3、探究性作业:等腰三角形两腰上的中线有什么关系吗?两腰上的高呢?利用类似的方法,还可以得到等腰三角形中哪些线段相等?
