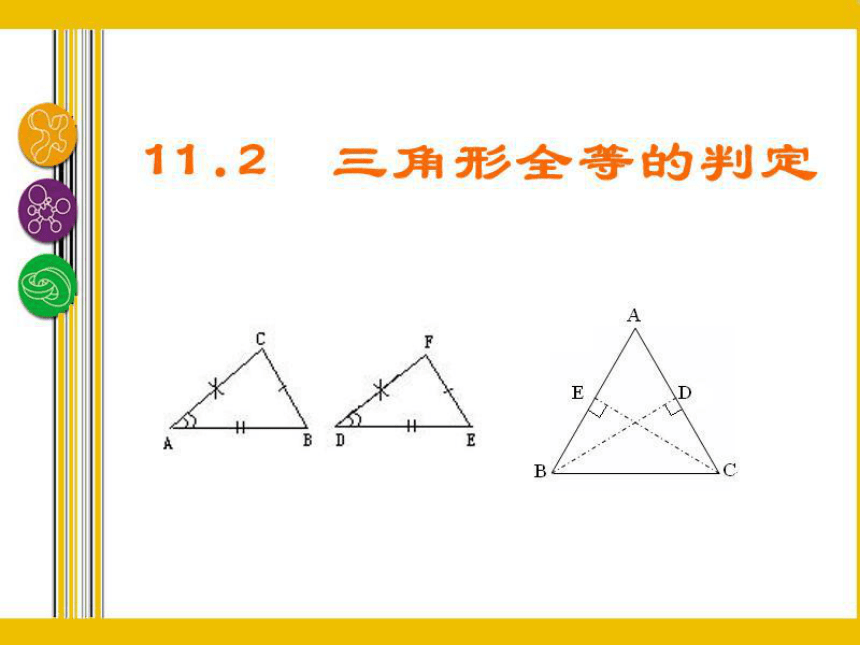
八年级数学《11.2 三角形全等的判定》课件
文档属性
| 名称 | 八年级数学《11.2 三角形全等的判定》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 722.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 22:44:43 | ||
图片预览






文档简介
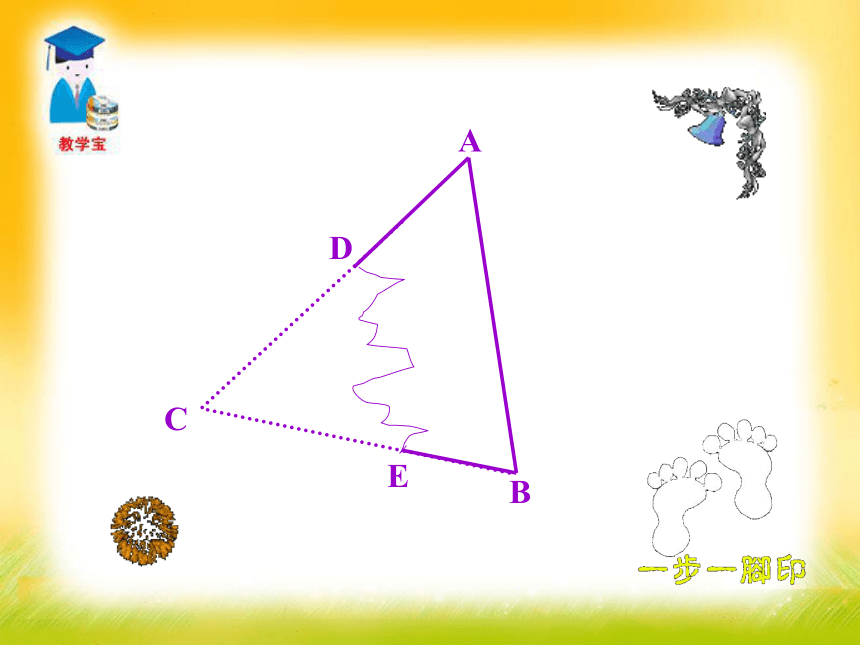
课件66张PPT。11.2全等三角形的判定 一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一个与原来同样大小的新教具吗?怎样才能保证制作的新教具与原来的全等呢?怎么办?可以帮帮我吗?新课导入CBEAD 1.了解三角形的稳定性;
2.掌握三角形全等的条件:边边边、边角边、角边角、角角边;
3.能运用全等三角形的条件,解决简单的推理证明问题.知识与能力教学目标 1.培养空间观念,推理能力,发展有条理地表达能力;
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.过程与方法 1.经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心;
2.通过课堂学习培养敢于实践,勇于发现,大胆探索,合作创新的精神;
3.在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.情感态度与价值观 1.运用直角三角形全等的条件解决一些实际问题;
2.三角形全等的条件.重点教学重难点 1.寻求三角形全等的条件;
2.灵活运用三角形全等条件;
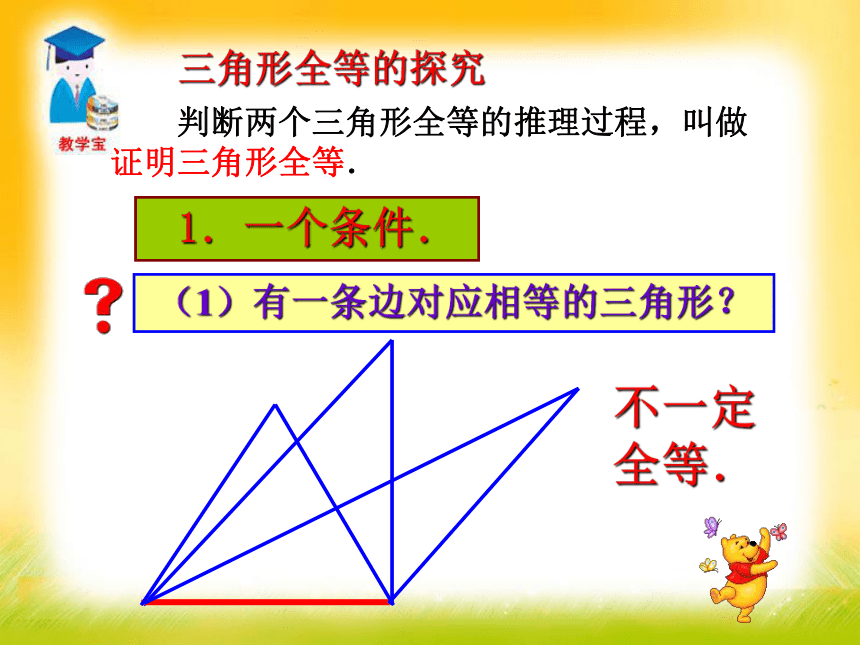
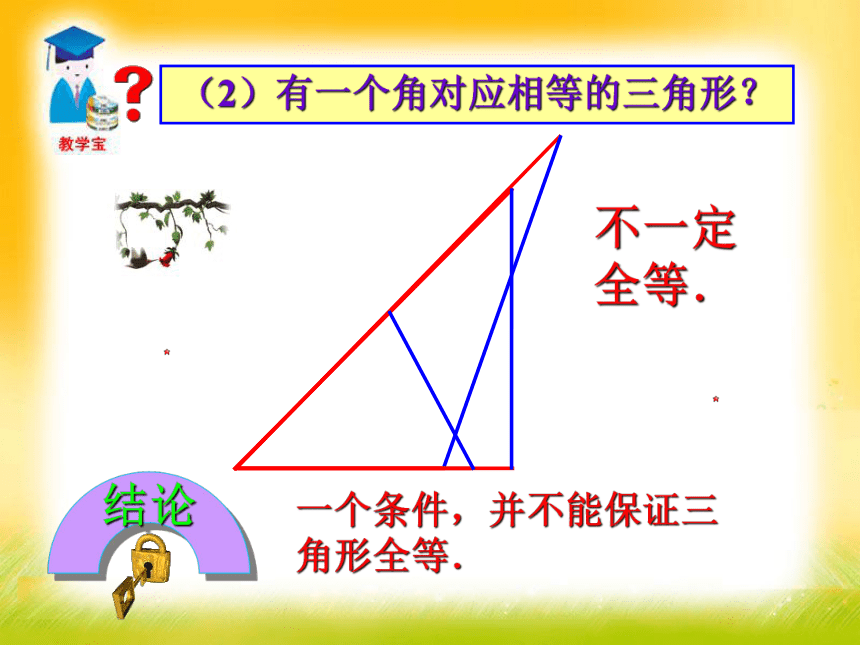
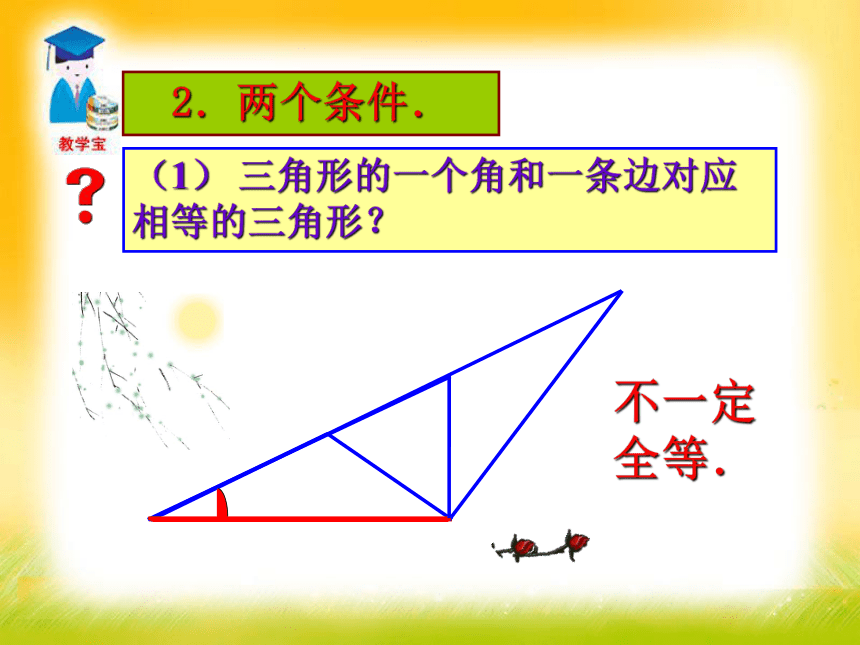
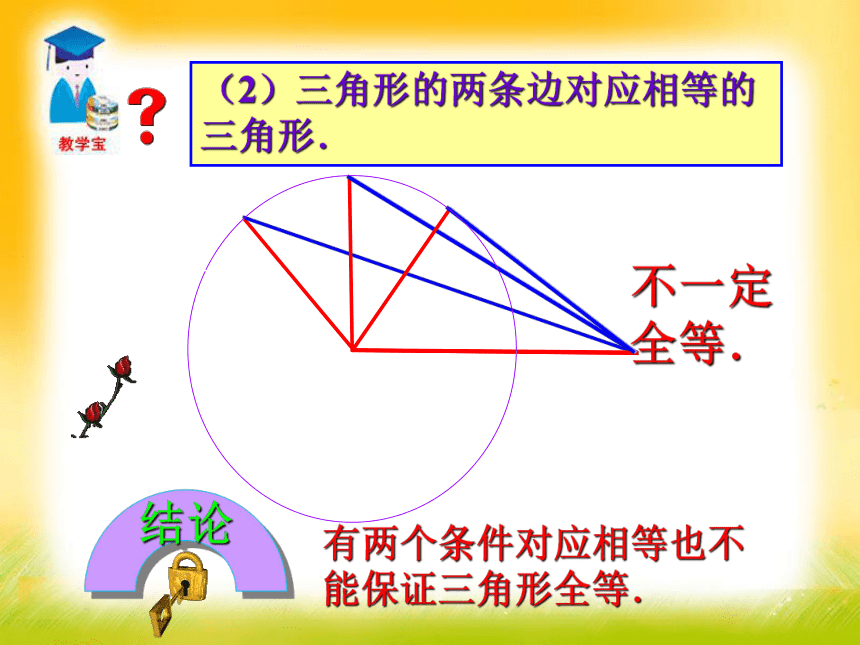
3.熟练运用直角三角形全等的条件解决一些实际问题.难点 1.一个条件.(1)有一条边对应相等的三角形?不一定全等.三角形全等的探究 判断两个三角形全等的推理过程,叫做证明三角形全等.(2)有一个角对应相等的三角形?一个条件,并不能保证三角形全等.不一定全等.结论不一定全等.(1) 三角形的一个角和一条边对应相等的三角形?2.两个条件.(2)三角形的两条边对应相等的三角形.不一定全等.有两个条件对应相等也不能保证三角形全等.结论已知△ABC,画一个△DEF,使 DE=AB,EF=BC,DF=AC.1.画线段DE=AB;2.分别以D、E为圆心,线段AC、
BC为半径画弧,两弧交于点F;3.连接线段DF、EF.DEF(1) 三角形的三条边分别对应相等的三角形? 3.三个条件.知识要点三角形全等的条件:三边对应相等的两个三角形全等.即:“边边边” 或“ SSS ”AB=A’B’BC=B’C’AC=A’C’(SSS)在△ABC和△A’B’C’中∴△ABC ≌△A’B’C’用符号语言表达为: 例1 已知△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABD≌△ACD. 在△ABC中,AB =AC,D是BC中点,点E在AD上.找出图中全等的三角形,并说明它们为什么是全等的?D想一想BCAE1.已知:如图,AB=AD,CB=CD. 求证: ∠B= ∠D.在△ABC和△ADC中,∴ △ABC≌ △ADC(SSS).∴ ∠B= ∠D(全等三角形的对应角相等).证明:连结AC,AB=AD, CB=CD, AC=AC(公共边),练一练证明:∵BE=CF(已知),即 BC=EF.在△ABC和△DEF中,AB=DE(已知),AC=BF(已知),BC=EF(已证),∴△ABC≌△DEF(SSS).∴∠A=∠D(全等三角形对应角相等).∴ BE+EC=CF+EC,2.如图,已知点B、E、C、F在同一条直线
上,AB=DE,AC=DF,BE=CF.求证:
∠A=∠D.(2) 三角形的两条边和它们的夹角对应相等的三角形? 已知△ABC,画一个△ A'B'C' ,使 A'B' =AB,B'C' =BC, ∠ B' =∠B.ABC1.画∠B’ =∠B;2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.3.连接A’C’.以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O 于点P;以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;过点Q画射线B’F,则∠OB’F =∠BA’B’C’MNOPQF··知识要点“边角边” 或“ SAS ”两边和它们的夹角对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
AC=DF,∴△ABC≌△DEF(SAS). 例2 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?证明:在△ABC和△DEC中,CA=CD,
∠ACB=∠DCE,
CB=CE,∴△ABC≌△DEC(SAS),∴AB=DE.证明:在?ABC 和?ADC中,AB = AD (已知),CB = CD(已知),AC = AC (公共边) ∴ ?ABC ≌ ?ADC(SSS), ∴ ∠BAO = ∠DAO (全等三角形的对应角相等).如右图,已知:AB=AD,CB=CD.
求证:AC⊥BD.练一练在?ABO 和?ADO中,AB = AD (已知), ∠BAO = ∠DAO (已证),AO= AO (公共边), ∴ ?ABO ≌ ?ADO(SAS), ∴ ∠AOB = ∠AOD (全等三角形的对应角相等). ∴ ∠AOB = ∠AOD=90°. ∴AC⊥BD(垂直定义). 又∵∠AOB + ∠AOD =180°(邻补角定义),知识要点 因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决.(3)三角形的两个边和其中一个边的对角对应相等的三角形?两个边和其中一个边的对角对应相等的三角形不一定全等.结论(4)三角形的三个角对应相等的三角形?三个内角对应相等的三角形不一定全等.结论两种情况①两个角及这两角的夹边分别对应相等②两个角及其中一角的对边分别对应相等(5) 三角形的两角和一条边对应相等的三角形.已知:任意△ABC,画一个△A’B’C’,使A’B’ =AB,∠A’ =∠A,∠B’=∠B.画法:
1.画A’B’=AB,
2.在A’B’的同旁画∠DA’B’ =∠A ,∠E B’A’ =∠B,A’D、B’E交于点C’.
∴△A’B’C’就是所要画的三角形.A'B’C’DE①两个角及这两角的夹边分别对应相等的三角形?知识要点“角边角”或“ASA”有两角和它们夹边对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
∠B=∠E, ∴△ABC≌△DEF(ASA).ABDECF②两个角及其中一角的对边分别对应相等的三角形.ABDECF知识要点“角角边”或“AAS”有两个角及其中一角的对边分别对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
∠C=∠F, ∴△ABC≌△DEF(AAS).ABDECF∴ AD = AE(全等三角形的对应边相等),
又 ∵ AB = AC(已知 ),
∴ AB – AD = AC – AE.
即:BD = CE.证明:在△ABE 和△ACD中
∠A =∠A(公共角),
AB = AC( 已知 ),
∠B =∠C( 已知 ), ∴△ABE≌△ACD(ASA), 例3 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:BD = CE.1.已知:如图,点B,F,C,E在同一条直
线,FB=CE,AB∥ED,AC∥FD,
求证:AB=DE,AC=DF.练一练 证明:∵FB=CE(已知),∴BC=EF. ∵AB∥ED,AC∥FD(已知), ∴∠B=∠E,∠ACB=∠DFE(两直线平行,内错角相等). 在△ABC与△DEF中,BC=EF(已证),∠B=∠E(已证),∠ACB=∠DFE(已证), ∴△ABC≌△DEF(ASA), ∴AB=DE,AC=DF(全等三角形对应边相等).2.已知:如右图,AB、CD相交于点O,
AC∥DB,OC = OD, E、F为 AB上两
点,且AE = BF.求证:CE=DF.证明:在?AOC 和?BOD中,∵ AC∥DB, ∴∠A = ∠B ( 两直线平等,内错角相等 ).又∵ ∠AOC = ∠BOD(对顶角相等),∠A = ∠B ( 已证 ),OC = OD(已知), ∴ ?AOC ≌ ?BOD(AAS). ∴ AC = BD.在?AEC 和?BFD中, AC = BD(已证),∠A = ∠B (已证),AE = BF(已知), ∴ ?AEC ≌ ?BFD(ASA), ∴ CE = DF.3.已知:AB ∥DE, AB=DE, ∠1=∠2
求证:BG=DF (中考题)提示:证△ABF和△EDG全等. 一同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的?想一想 判定一般三角形全等的方法有哪几种?若这两个三角形是直角三角形,那么这些判定方法适用吗?判定直角三角形全等有特殊方法吗?答:SSS,SAS,ASA,AAS.想一想Rt△ABC≌ Rt△A'B'C' 画法:1.画∠MC'N=90°.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
4.连接A'B'.一条直角边和斜边对应相等的直角三角形全等吗?知识要点“斜边、直角边公理”或“HL”斜边和一直角边对应相等的两个直角三角形全等.直角三角形全等的条件:用符号语言表达为:在Rt△ABC与Rt△DEF中,AC=DF,
BC=EF, ∴Rt△ABC≌Rt△DEF(AAS). 如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )ASASASAAS×想一想 1.直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“HL”公理. 2.使用“HL”公理时,必须先得出两个直角三角形,然后证明斜边和一直角边对应相等.注意 4.直角三角形全等的判定方法有五项依据:“SAS”、“ASA”、“ AAS”、“SSS”、“HL”其中,“HL”公理只适用于判定直角三角形全等. 3.两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对边相等).三边对应相等 (SSS)
一锐角和它的邻边对应相等 (ASA)
一锐角和它的对边对应相等 (AAS)
两直角边对应相等 (SAS)
斜边和一条直角边对应相等 (HL)判断三角形全等的条件课堂小结∴△ABC≌△DCB (SSS) . 1.如图,AB=CD,AC=BD,△ABC和△DCB
是否全等?试说明理由. 随堂练习2.如图,D、F是线段BC上的两点,AB=EC,
AF=ED,要使△ABF≌△ECD ,还需要条
件___________________.BF=CD 或 BD=CF3.已知:如图,AB=CB,∠ABD = ∠CBD.
问AD=CD,BD 平分∠ADC吗?证明:在△ABD与△CBD中,AB=CB,
∠ABD=∠CBD,
BD=BD,∴△ABD≌△CBD(SAS).∴AD=CD,∠ADB=∠CDB,即BD平分∠ADC.4.如图,点E、F在BC上,BE=CF,AB=
DC,∠B=∠C,求证:∠A=∠D. 证明:∵BF=BE+EF,CE=CF+FE,而BE=CF,
∴BF=CE.在△ABF和△DCE中,BF=CE,
∠B=∠C,
AB=DC,∴△BAD≌△BAC (SAS),∴∠A=∠D.5.如图,B点在A点的正北方向.两车从路段
AB的一端A出发,分别向东、向西进行相
同的距离,到达C、D两地.此时C、D到B
的距离相等吗?证明:∵在△BAD和△BAC中,BA=BA,
∠BAD=∠BAC,
AD=AC,则△BAD≌△BAC(SAS).∴BD=BC,
∴C、D到B的距离相等.6.已知:如图,在△ABC和△A′B′C′中,
CD、C′D′分别是高,并且AC=A′C′,
CD=C′D′,∠ACB=∠A′C′B′.
求证:△ABC≌△A′B′C′.7.如图:已知△ABC≌△A1B1C1,AD、A1D1分
别是∠BAC和∠B1 A1 C1的角平分线.求证:
AD= A1D1 .8.如图,已知:AB∥CD,AB=CD,点B、
E、F、D在同一直线上,∠A=∠C,
求证:AE=CF.9.如图,AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.10.如图,C是路段AB的中点,两人从C同
时出发,以相同的速度分别沿着两条直
线行走,并同时到达D、E 两地.DA⊥
AB,EB⊥AB. D、E与路段AB的距离
相等吗?为什么? 习题答案3.可先证明△ABE≌△ACD.
4.只要测量A′B′.证明△AOB ≌
△AO′B′.
5.可先证明△ABC≌△ABD.
6.可先证明△ACD≌△BCE.7.可先证明△ABD≌△ACD.
8.可先证明△ABC≌△DCB,得∠ABC
=∠DCB;再证∠ABD=∠ACD.
9.可先证明△ABC≌△DEF.10.可先证明△AOB≌△COD,得
∠B=∠D.
11. 可先证明△ABC≌△DEF.
12.可先证明△ADE≌△CFE.
13.△ABD≌△ACD,△ABE≌△ACE,
△BDE≌△CDE .
2.掌握三角形全等的条件:边边边、边角边、角边角、角角边;
3.能运用全等三角形的条件,解决简单的推理证明问题.知识与能力教学目标 1.培养空间观念,推理能力,发展有条理地表达能力;
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.过程与方法 1.经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心;
2.通过课堂学习培养敢于实践,勇于发现,大胆探索,合作创新的精神;
3.在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.情感态度与价值观 1.运用直角三角形全等的条件解决一些实际问题;
2.三角形全等的条件.重点教学重难点 1.寻求三角形全等的条件;
2.灵活运用三角形全等条件;
3.熟练运用直角三角形全等的条件解决一些实际问题.难点 1.一个条件.(1)有一条边对应相等的三角形?不一定全等.三角形全等的探究 判断两个三角形全等的推理过程,叫做证明三角形全等.(2)有一个角对应相等的三角形?一个条件,并不能保证三角形全等.不一定全等.结论不一定全等.(1) 三角形的一个角和一条边对应相等的三角形?2.两个条件.(2)三角形的两条边对应相等的三角形.不一定全等.有两个条件对应相等也不能保证三角形全等.结论已知△ABC,画一个△DEF,使 DE=AB,EF=BC,DF=AC.1.画线段DE=AB;2.分别以D、E为圆心,线段AC、
BC为半径画弧,两弧交于点F;3.连接线段DF、EF.DEF(1) 三角形的三条边分别对应相等的三角形? 3.三个条件.知识要点三角形全等的条件:三边对应相等的两个三角形全等.即:“边边边” 或“ SSS ”AB=A’B’BC=B’C’AC=A’C’(SSS)在△ABC和△A’B’C’中∴△ABC ≌△A’B’C’用符号语言表达为: 例1 已知△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABD≌△ACD. 在△ABC中,AB =AC,D是BC中点,点E在AD上.找出图中全等的三角形,并说明它们为什么是全等的?D想一想BCAE1.已知:如图,AB=AD,CB=CD. 求证: ∠B= ∠D.在△ABC和△ADC中,∴ △ABC≌ △ADC(SSS).∴ ∠B= ∠D(全等三角形的对应角相等).证明:连结AC,AB=AD, CB=CD, AC=AC(公共边),练一练证明:∵BE=CF(已知),即 BC=EF.在△ABC和△DEF中,AB=DE(已知),AC=BF(已知),BC=EF(已证),∴△ABC≌△DEF(SSS).∴∠A=∠D(全等三角形对应角相等).∴ BE+EC=CF+EC,2.如图,已知点B、E、C、F在同一条直线
上,AB=DE,AC=DF,BE=CF.求证:
∠A=∠D.(2) 三角形的两条边和它们的夹角对应相等的三角形? 已知△ABC,画一个△ A'B'C' ,使 A'B' =AB,B'C' =BC, ∠ B' =∠B.ABC1.画∠B’ =∠B;2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.3.连接A’C’.以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O 于点P;以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;过点Q画射线B’F,则∠OB’F =∠BA’B’C’MNOPQF··知识要点“边角边” 或“ SAS ”两边和它们的夹角对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
AC=DF,∴△ABC≌△DEF(SAS). 例2 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?证明:在△ABC和△DEC中,CA=CD,
∠ACB=∠DCE,
CB=CE,∴△ABC≌△DEC(SAS),∴AB=DE.证明:在?ABC 和?ADC中,AB = AD (已知),CB = CD(已知),AC = AC (公共边) ∴ ?ABC ≌ ?ADC(SSS), ∴ ∠BAO = ∠DAO (全等三角形的对应角相等).如右图,已知:AB=AD,CB=CD.
求证:AC⊥BD.练一练在?ABO 和?ADO中,AB = AD (已知), ∠BAO = ∠DAO (已证),AO= AO (公共边), ∴ ?ABO ≌ ?ADO(SAS), ∴ ∠AOB = ∠AOD (全等三角形的对应角相等). ∴ ∠AOB = ∠AOD=90°. ∴AC⊥BD(垂直定义). 又∵∠AOB + ∠AOD =180°(邻补角定义),知识要点 因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决.(3)三角形的两个边和其中一个边的对角对应相等的三角形?两个边和其中一个边的对角对应相等的三角形不一定全等.结论(4)三角形的三个角对应相等的三角形?三个内角对应相等的三角形不一定全等.结论两种情况①两个角及这两角的夹边分别对应相等②两个角及其中一角的对边分别对应相等(5) 三角形的两角和一条边对应相等的三角形.已知:任意△ABC,画一个△A’B’C’,使A’B’ =AB,∠A’ =∠A,∠B’=∠B.画法:
1.画A’B’=AB,
2.在A’B’的同旁画∠DA’B’ =∠A ,∠E B’A’ =∠B,A’D、B’E交于点C’.
∴△A’B’C’就是所要画的三角形.A'B’C’DE①两个角及这两角的夹边分别对应相等的三角形?知识要点“角边角”或“ASA”有两角和它们夹边对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
∠B=∠E, ∴△ABC≌△DEF(ASA).ABDECF②两个角及其中一角的对边分别对应相等的三角形.ABDECF知识要点“角角边”或“AAS”有两个角及其中一角的对边分别对应相等的两个三角形全等.三角形全等的条件:用符号语言表达为:在△ABC与△DEF中,AB=DE,
∠A=∠D,
∠C=∠F, ∴△ABC≌△DEF(AAS).ABDECF∴ AD = AE(全等三角形的对应边相等),
又 ∵ AB = AC(已知 ),
∴ AB – AD = AC – AE.
即:BD = CE.证明:在△ABE 和△ACD中
∠A =∠A(公共角),
AB = AC( 已知 ),
∠B =∠C( 已知 ), ∴△ABE≌△ACD(ASA), 例3 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:BD = CE.1.已知:如图,点B,F,C,E在同一条直
线,FB=CE,AB∥ED,AC∥FD,
求证:AB=DE,AC=DF.练一练 证明:∵FB=CE(已知),∴BC=EF. ∵AB∥ED,AC∥FD(已知), ∴∠B=∠E,∠ACB=∠DFE(两直线平行,内错角相等). 在△ABC与△DEF中,BC=EF(已证),∠B=∠E(已证),∠ACB=∠DFE(已证), ∴△ABC≌△DEF(ASA), ∴AB=DE,AC=DF(全等三角形对应边相等).2.已知:如右图,AB、CD相交于点O,
AC∥DB,OC = OD, E、F为 AB上两
点,且AE = BF.求证:CE=DF.证明:在?AOC 和?BOD中,∵ AC∥DB, ∴∠A = ∠B ( 两直线平等,内错角相等 ).又∵ ∠AOC = ∠BOD(对顶角相等),∠A = ∠B ( 已证 ),OC = OD(已知), ∴ ?AOC ≌ ?BOD(AAS). ∴ AC = BD.在?AEC 和?BFD中, AC = BD(已证),∠A = ∠B (已证),AE = BF(已知), ∴ ?AEC ≌ ?BFD(ASA), ∴ CE = DF.3.已知:AB ∥DE, AB=DE, ∠1=∠2
求证:BG=DF (中考题)提示:证△ABF和△EDG全等. 一同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的?想一想 判定一般三角形全等的方法有哪几种?若这两个三角形是直角三角形,那么这些判定方法适用吗?判定直角三角形全等有特殊方法吗?答:SSS,SAS,ASA,AAS.想一想Rt△ABC≌ Rt△A'B'C' 画法:1.画∠MC'N=90°.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
4.连接A'B'.一条直角边和斜边对应相等的直角三角形全等吗?知识要点“斜边、直角边公理”或“HL”斜边和一直角边对应相等的两个直角三角形全等.直角三角形全等的条件:用符号语言表达为:在Rt△ABC与Rt△DEF中,AC=DF,
BC=EF, ∴Rt△ABC≌Rt△DEF(AAS). 如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )ASASASAAS×想一想 1.直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法——“HL”公理. 2.使用“HL”公理时,必须先得出两个直角三角形,然后证明斜边和一直角边对应相等.注意 4.直角三角形全等的判定方法有五项依据:“SAS”、“ASA”、“ AAS”、“SSS”、“HL”其中,“HL”公理只适用于判定直角三角形全等. 3.两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只须找两个条件(两个条件中至少有一个条件是一对边相等).三边对应相等 (SSS)
一锐角和它的邻边对应相等 (ASA)
一锐角和它的对边对应相等 (AAS)
两直角边对应相等 (SAS)
斜边和一条直角边对应相等 (HL)判断三角形全等的条件课堂小结∴△ABC≌△DCB (SSS) . 1.如图,AB=CD,AC=BD,△ABC和△DCB
是否全等?试说明理由. 随堂练习2.如图,D、F是线段BC上的两点,AB=EC,
AF=ED,要使△ABF≌△ECD ,还需要条
件___________________.BF=CD 或 BD=CF3.已知:如图,AB=CB,∠ABD = ∠CBD.
问AD=CD,BD 平分∠ADC吗?证明:在△ABD与△CBD中,AB=CB,
∠ABD=∠CBD,
BD=BD,∴△ABD≌△CBD(SAS).∴AD=CD,∠ADB=∠CDB,即BD平分∠ADC.4.如图,点E、F在BC上,BE=CF,AB=
DC,∠B=∠C,求证:∠A=∠D. 证明:∵BF=BE+EF,CE=CF+FE,而BE=CF,
∴BF=CE.在△ABF和△DCE中,BF=CE,
∠B=∠C,
AB=DC,∴△BAD≌△BAC (SAS),∴∠A=∠D.5.如图,B点在A点的正北方向.两车从路段
AB的一端A出发,分别向东、向西进行相
同的距离,到达C、D两地.此时C、D到B
的距离相等吗?证明:∵在△BAD和△BAC中,BA=BA,
∠BAD=∠BAC,
AD=AC,则△BAD≌△BAC(SAS).∴BD=BC,
∴C、D到B的距离相等.6.已知:如图,在△ABC和△A′B′C′中,
CD、C′D′分别是高,并且AC=A′C′,
CD=C′D′,∠ACB=∠A′C′B′.
求证:△ABC≌△A′B′C′.7.如图:已知△ABC≌△A1B1C1,AD、A1D1分
别是∠BAC和∠B1 A1 C1的角平分线.求证:
AD= A1D1 .8.如图,已知:AB∥CD,AB=CD,点B、
E、F、D在同一直线上,∠A=∠C,
求证:AE=CF.9.如图,AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.10.如图,C是路段AB的中点,两人从C同
时出发,以相同的速度分别沿着两条直
线行走,并同时到达D、E 两地.DA⊥
AB,EB⊥AB. D、E与路段AB的距离
相等吗?为什么? 习题答案3.可先证明△ABE≌△ACD.
4.只要测量A′B′.证明△AOB ≌
△AO′B′.
5.可先证明△ABC≌△ABD.
6.可先证明△ACD≌△BCE.7.可先证明△ABD≌△ACD.
8.可先证明△ABC≌△DCB,得∠ABC
=∠DCB;再证∠ABD=∠ACD.
9.可先证明△ABC≌△DEF.10.可先证明△AOB≌△COD,得
∠B=∠D.
11. 可先证明△ABC≌△DEF.
12.可先证明△ADE≌△CFE.
13.△ABD≌△ACD,△ABE≌△ACE,
△BDE≌△CDE .
