八年级数学《11.3 角平分线的性质》课件
文档属性
| 名称 | 八年级数学《11.3 角平分线的性质》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 00:00:00 | ||
图片预览






文档简介
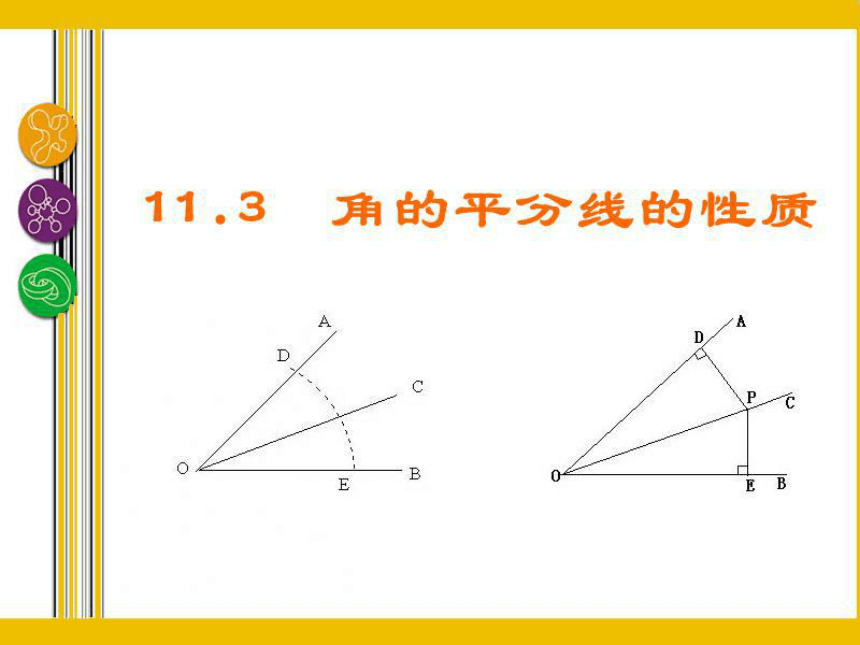
课件32张PPT。11.3角的平分线性质 在纸上任意画一个角,用剪刀剪下,用折纸的方法,试确定角的平分线.
你能发现什么吗?新课导入动动手 1.会用尺规作一个已知角的平分线;
2.掌握角平分线的性质.知识与能力教学目标 1.在探究作已知角的平分线的方法和角平分线的性质的过程中,发展几何直觉;
2.提高综合运用三角形全等的有关知识解决实际问题的能力;
3.掌握简单的角平分线在生产、生活中的应用.过程与方法 1.在探究作角的平分线的过程中,培养探究的兴趣,增强解决问题的信心,获得解决问题的成功体验;
2.通过合作、交流、讨论,增强合作、沟通能力.情感态度与价值观 1.掌握角平分线的性质定理及其逆定理;
2.角平分线性质的证明及运用. 1.角平分线性质的探究;
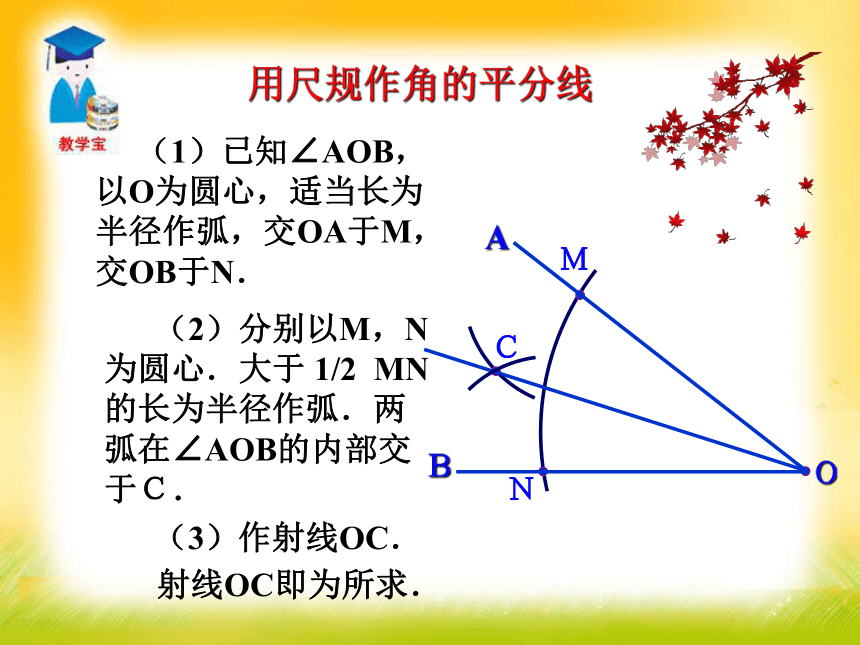
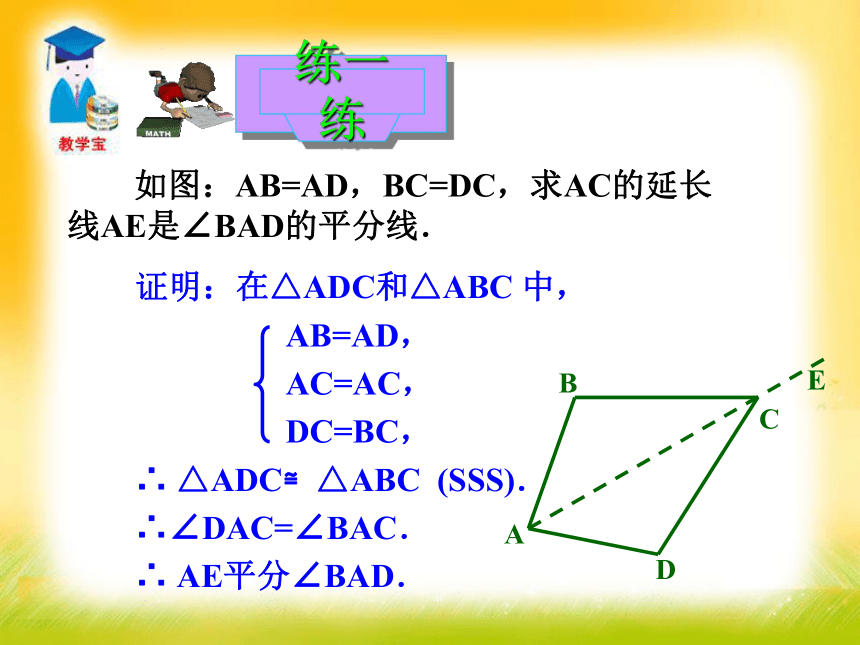
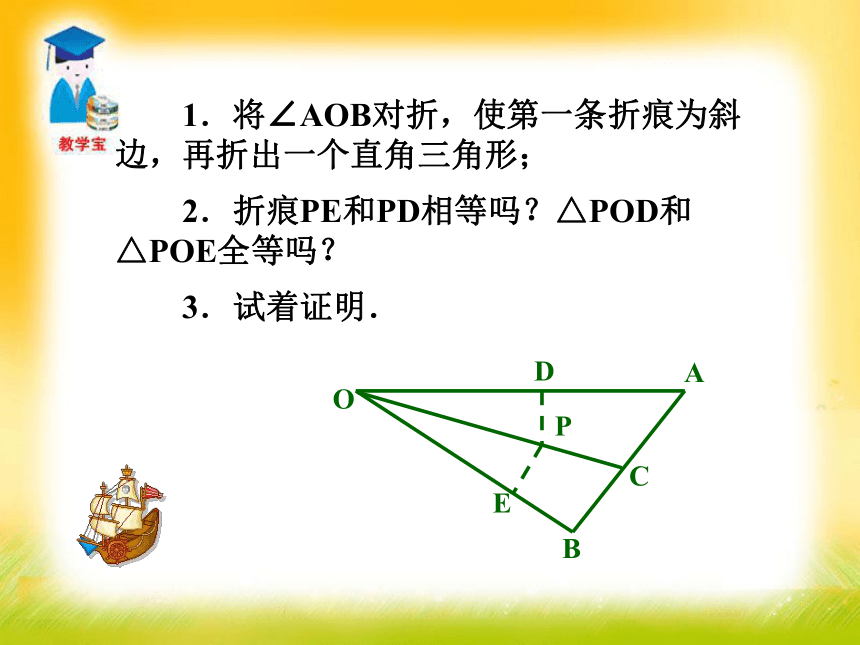
2.角平分线性质定理及其逆定理的证明及应用.重点难点教学重难点 已知一个角,怎样将它平分呢?想一想MN (1)已知∠AOB,以O为圆心,适当长为半径作弧,交OA于M,交OB于N. (2)分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.(3)作射线OC.射线OC即为所求.用尺规作角的平分线 如图:AB=AD,BC=DC,求AC的延长线AE是∠BAD的平分线.练一练 1.将∠AOB对折,使第一条折痕为斜边,再折出一个直角三角形;
2.折痕PE和PD相等吗?△POD和△POE全等吗?
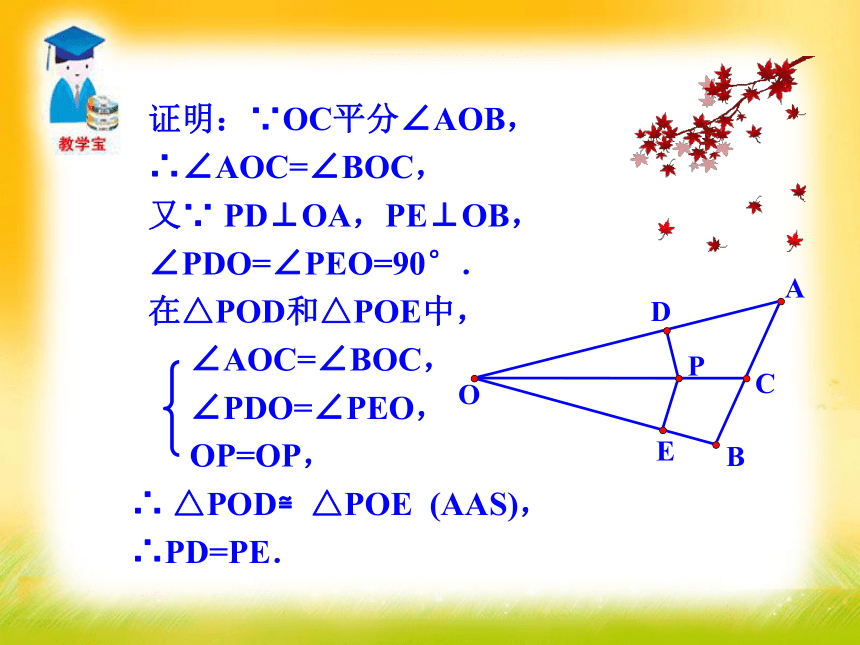
3.试着证明.知识要点 角的平分线上的点到角的两边的距离相等.角的平分线的性质: ∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上,
∴ QD = QE.证明:∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义). 在Rt△QDO和Rt△QEO中,
QO=QO(公共边), QD=QE, ∴ Rt△QDO≌Rt△QEO(HL),
∴ ∠ QOD=∠QOE,
∴点Q在∠AOB的平分线上. 例1 已知:如图,QD⊥OA,QE⊥ OB,点D、E为垂足,QD = QE.求证:点Q在∠AOB的平分线上. 角的内部到角的两边的距离相等的点在角的平分线上.∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.用数学语言表示为:结论 证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等. 例3 如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB、BC、CA的距离相等. 内心:三角形的三内角平分线交于一点,这点叫做三角形的内心.
三角形的内心到三角形三边的距离相等.知识要点三角形的五心: 旁心:三角形的一内角平分线和另外两顶点处的外角平分线交于一点,这点叫做三角形的旁心.
三角形有三个旁心.
三角形的内心到三角形三边的距离相等. 重心:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,上述交点叫做三角形的重心. 垂心:三角形的三条高交于一点,这点叫做三角形的垂心.练一练 如图,已知△ABC的外角∠DAB和∠ABE的平分线相交于点F,
求证:点F在∠DCE的平分线上. 证明:过点F作FG⊥AD于G,FH⊥BE于H,FM⊥AB于M, ∵点F在∠DAB的平分线上, FG⊥AD,FM⊥AB,∴FG=FM. 又∵点F在∠ABE的平分线上,FH⊥BE, FM⊥AB,∴FM=FH,∴FG=FH, ∴点F在∠DAE的平分线上. 如图,要在S区建一个贸易市场,使它到铁路和公路的距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1:20 000)想一想DC 解:作铁路和公路的夹角的角平分线OC,截取OD=2.5cm ,D即为所求.O 如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF,求证:CF=EB.练一练 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上.
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.课堂小结1.(1)∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________.(____________________
_________________)
(2)∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________.(____________________
_____________________________)∠1= ∠2DC=DE 到一个角的两边的距离相等的点,在这个角平分线上. 在角平分线上的点到角的两边的距离相等.随堂练习2.直线表示三条相互交叉的公路,现要建一
个货物中转站,要求它到三条公路的距离
相等,则可供选择的地址有:( ) A.一处 B. 两处
C.三处 D.四处D3.已知:BD⊥AM于点D,CE⊥AN于点E,
BD,CE交点F,CF=BF,求证:点F在
∠A的平分线上.提示:
证明△CDF≌△BEF.4.已知:如图,∠C= ∠C′=90° AC=AC ′
求证:(1) ∠ABC= ∠ABC ′ ;
(2)BC=BC ′ .(要求不用三角形全等的
判定)证明:
提示:利用角平分线定理.1.证明△OMP≌△ONP.
2.证明△BDE≌△CDF.
3.证明△DOB≌△EOC.
4.证明△EPD≌△FPD.
5.证明△PDF≌△PEF.
6.证明△DEG≌△DFG,得∠EGD=∠FGD.习题答案
你能发现什么吗?新课导入动动手 1.会用尺规作一个已知角的平分线;
2.掌握角平分线的性质.知识与能力教学目标 1.在探究作已知角的平分线的方法和角平分线的性质的过程中,发展几何直觉;
2.提高综合运用三角形全等的有关知识解决实际问题的能力;
3.掌握简单的角平分线在生产、生活中的应用.过程与方法 1.在探究作角的平分线的过程中,培养探究的兴趣,增强解决问题的信心,获得解决问题的成功体验;
2.通过合作、交流、讨论,增强合作、沟通能力.情感态度与价值观 1.掌握角平分线的性质定理及其逆定理;
2.角平分线性质的证明及运用. 1.角平分线性质的探究;
2.角平分线性质定理及其逆定理的证明及应用.重点难点教学重难点 已知一个角,怎样将它平分呢?想一想MN (1)已知∠AOB,以O为圆心,适当长为半径作弧,交OA于M,交OB于N. (2)分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.(3)作射线OC.射线OC即为所求.用尺规作角的平分线 如图:AB=AD,BC=DC,求AC的延长线AE是∠BAD的平分线.练一练 1.将∠AOB对折,使第一条折痕为斜边,再折出一个直角三角形;
2.折痕PE和PD相等吗?△POD和△POE全等吗?
3.试着证明.知识要点 角的平分线上的点到角的两边的距离相等.角的平分线的性质: ∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上,
∴ QD = QE.证明:∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义). 在Rt△QDO和Rt△QEO中,
QO=QO(公共边), QD=QE, ∴ Rt△QDO≌Rt△QEO(HL),
∴ ∠ QOD=∠QOE,
∴点Q在∠AOB的平分线上. 例1 已知:如图,QD⊥OA,QE⊥ OB,点D、E为垂足,QD = QE.求证:点Q在∠AOB的平分线上. 角的内部到角的两边的距离相等的点在角的平分线上.∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.用数学语言表示为:结论 证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等. 例3 如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB、BC、CA的距离相等. 内心:三角形的三内角平分线交于一点,这点叫做三角形的内心.
三角形的内心到三角形三边的距离相等.知识要点三角形的五心: 旁心:三角形的一内角平分线和另外两顶点处的外角平分线交于一点,这点叫做三角形的旁心.
三角形有三个旁心.
三角形的内心到三角形三边的距离相等. 重心:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,上述交点叫做三角形的重心. 垂心:三角形的三条高交于一点,这点叫做三角形的垂心.练一练 如图,已知△ABC的外角∠DAB和∠ABE的平分线相交于点F,
求证:点F在∠DCE的平分线上. 证明:过点F作FG⊥AD于G,FH⊥BE于H,FM⊥AB于M, ∵点F在∠DAB的平分线上, FG⊥AD,FM⊥AB,∴FG=FM. 又∵点F在∠ABE的平分线上,FH⊥BE, FM⊥AB,∴FM=FH,∴FG=FH, ∴点F在∠DAE的平分线上. 如图,要在S区建一个贸易市场,使它到铁路和公路的距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1:20 000)想一想DC 解:作铁路和公路的夹角的角平分线OC,截取OD=2.5cm ,D即为所求.O 如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF,求证:CF=EB.练一练 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上.
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.课堂小结1.(1)∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________.(____________________
_________________)
(2)∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________.(____________________
_____________________________)∠1= ∠2DC=DE 到一个角的两边的距离相等的点,在这个角平分线上. 在角平分线上的点到角的两边的距离相等.随堂练习2.直线表示三条相互交叉的公路,现要建一
个货物中转站,要求它到三条公路的距离
相等,则可供选择的地址有:( ) A.一处 B. 两处
C.三处 D.四处D3.已知:BD⊥AM于点D,CE⊥AN于点E,
BD,CE交点F,CF=BF,求证:点F在
∠A的平分线上.提示:
证明△CDF≌△BEF.4.已知:如图,∠C= ∠C′=90° AC=AC ′
求证:(1) ∠ABC= ∠ABC ′ ;
(2)BC=BC ′ .(要求不用三角形全等的
判定)证明:
提示:利用角平分线定理.1.证明△OMP≌△ONP.
2.证明△BDE≌△CDF.
3.证明△DOB≌△EOC.
4.证明△EPD≌△FPD.
5.证明△PDF≌△PEF.
6.证明△DEG≌△DFG,得∠EGD=∠FGD.习题答案
