2021-2022学年山东省滕州市洪绪镇洪绪中学北师大版九年级数学下册2.2二次函数图像与性质综合检测题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年山东省滕州市洪绪镇洪绪中学北师大版九年级数学下册2.2二次函数图像与性质综合检测题(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 333.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 10:51:39 | ||
图片预览




文档简介
洪绪中学九年级数学二次函数图像与性质综合检测题
一.选择题
1.如果y=(m﹣2)是关于x的二次函数,则m=( )
A.﹣1 B.2 C.﹣1或2 D.m不存在
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
4.二次函数y=﹣x2﹣2x+1图象的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线y=x2﹣x﹣6与x轴的交点坐标是( )
A.(3,0) B.(﹣2,0)
C.(﹣6,0),(1,0) D.(3,0),(﹣2,0)
6.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
7.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
A. B. C. D.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
9.如图,对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,a≠0),则下列结论:①abc>0,②b2>4ac,③4a+2b+c<0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x>0时,y随x的增大而增大,正确的个数为( )
A.2 B.3 C.4 D.5
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )
A.5 B. C.4 D.
二.填空题
11.抛物线y=x2﹣2x+4的顶点坐标是 ,对称轴为 .
12.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0<x<2时,y关于x的函数解析式为 .
13.若抛物线y=(m﹣1)x2+2mx+2m﹣1的图象的最低点的纵坐标为零,则m= .
14.二次函数y=ax2﹣4x﹣13a有最小值﹣17,则a= .
15.如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
16.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
下列结论:①a>0;②当x<﹣2时,y的值随x的增大而减小;③方程ax2+bx+c=﹣5有两个不相等的实数根.④当x=﹣2时,函数有最小值﹣6.
其中,正确结论的序号是 (把所有正确结论的序号都填上).
三.解答题
17.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.
18.已知:在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
19.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
二次函数图像与性质综合检测题答案提示
一.选择题
1.如果y=(m﹣2)是关于x的二次函数,则m=( )
A.﹣1 B.2 C.﹣1或2 D.m不存在
解:令m2﹣m=2,解得m=2或m=﹣1,且m﹣2≠0,m≠2,因此m=﹣1,
故选:A.
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
解:因为抛物线y=x2向上平移2个单位,得到y=x2+2,
所以,开口方向相同;形状完全相同;对称轴相同.
正确的有三个,故选D.
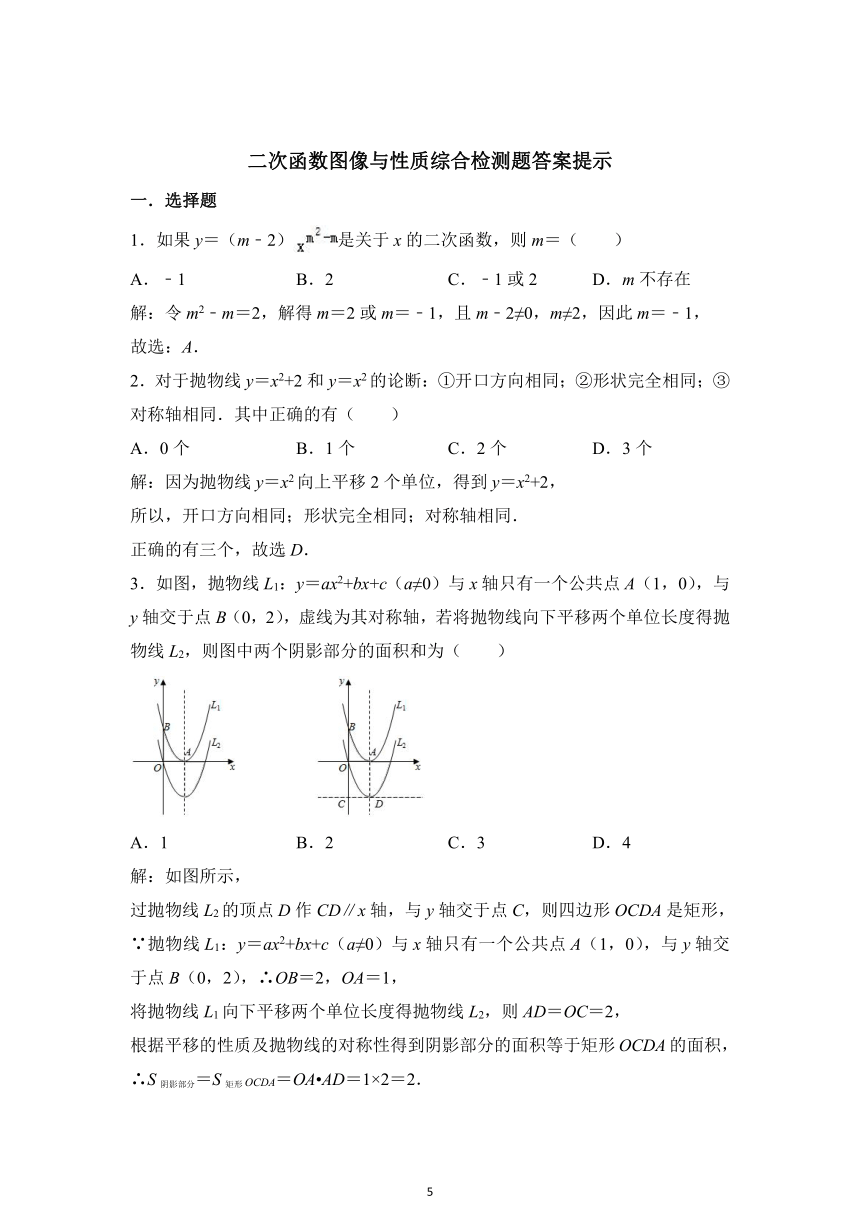
3.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
解:如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
故选:B.
4.二次函数y=﹣x2﹣2x+1图象的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵y=﹣x2﹣2x+1=﹣(x2+2x+1﹣1)+1=﹣(x+1)2+2,
∴顶点坐标为(﹣1,2),∴顶点在第二象限,
故选:B.
5.抛物线y=x2﹣x﹣6与x轴的交点坐标是( )
A.(3,0) B.(﹣2,0)
C.(﹣6,0),(1,0) D.(3,0),(﹣2,0)
解:令y=0,求出x的值为﹣2与3,故交点坐标为(3,0),(﹣2,0),
故选:D.
6.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
解:∵点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,∴a=0,∴n=m2+4,∴m﹣n=m﹣(m2+4)=﹣m2+m﹣4=﹣(m﹣)2﹣,
∴当m=时,m﹣n取得最大值,此时m﹣n=﹣,
故选:C.
7.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
A. B. C. D.
解:A、由一次函数y=ax+c图象,得a>0,c<0,由二次函数y=ax2+bx+c图象,得a<0,c>0,故A错误;
B、由一次函数y=ax+c图象,得a>0,c>0,由二次函数y=ax2+bx+c图象,得a>0,c<0,故B错误;
C、由一次函数y=ax+c图象,得a<0,c>0,由二次函数y=ax2+bx+c图象,得a<0,c>0,故C正确;
D、由一次函数y=ax+c图象,得a<0,c>0,由二次函数y=ax2+bx+c图象,得a>0,c>0,故D错误;
故选:C.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
解:①∵由抛物线的开口向上知a>0,∵对称轴位于y轴的右侧,∴b<0.
∵抛物线与y轴交于负半轴,∴c<0,∴abc>0;故错误;
②对称轴为直线x=﹣<1,得2a>﹣b,即2a+b>0,故错误;
③如图,当x=﹣2时,y>0,4a﹣2b+c>0,故正确;
④∵当x=﹣1时,y=0,∴0=a﹣b+c<a+2a+c=3a+c,即3a+c>0.故正确.
综上所述,有2个结论正确.故选:B.
9.如图,对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,a≠0),则下列结论:①abc>0,②b2>4ac,③4a+2b+c<0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x>0时,y随x的增大而增大,正确的个数为( )
A.2 B.3 C.4 D.5
解:①由图象可知:a>0,c<0,∵﹣=1,∴b=﹣2a<0,∴abc>0,故①正确;
②∵抛物线与x轴有两个交点,∴b2﹣4ac>0,∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③正确;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,∴3a+c>0,故④正确;
⑤当x=1时,y取到值最小,此时,y=a+b+c,而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,故a+b≤am2+bm,即a+b≤m(am+b),故⑤正确,
⑥当x>0时,y先随x的增大而减小,故⑥错误,故选:D.
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )
A.5 B. C.4 D.
解:如图,由题意可得,互异二次函数y=(x﹣m)2﹣m的顶点(m,﹣m)在直线y=﹣x上运动,
在正方形OABC中,点A(0,2),点C(2,0),
∴B(2,2),
从图象可以看出,当函数图象从左上向右下运动时,若抛物线与正方形有交点,先经过点A,再逐渐经过点O,点B,点C,最后再经过点B,且在运动的过程中,两次经过点A,两次经过点O,点B和点C,
∴只需算出当函数经过点A及点B时m的值,即可求出m的最大值及最小值.
当互异二次函数y=(x﹣m)2﹣m经过点A(0,2)时,m=2或m=﹣1;
当互异二次函数y=(x﹣m)2﹣m经过点B(2,2)时,m=或m=.
∴互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值分别是,﹣1.
∴最大值和最小值之差为﹣(﹣1)=,
故选:B.
二.填空题
11.抛物线y=x2﹣2x+4的顶点坐标是 (1,3) ,对称轴为 直线x=1 .
解:y=x2﹣2x+4=(x﹣1)2+3,
所以抛物线y=x2﹣2x+4的顶点坐标是(1,3),对称轴是直线x=1,
故答案为:(1,3),直线x=1.
12.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0<x<2时,y关于x的函数解析式为 y=(0<x<2) .
解:过点F作FM⊥AE,垂足为M,∵AF=EF,∴AM=ME,
在Rt△ABE中,AE==,∴AM=,
∵∠B=∠AMF=90°,∠FAM=∠AEB,∴△ABE∽△FMA,
∴=,即=,∴xy=,
即y=(0<x<2),故答案为:y=(0<x<2).
13.若抛物线y=(m﹣1)x2+2mx+2m﹣1的图象的最低点的纵坐标为零,则m= .
解:根据题意,根据函数的顶点的坐标公式得,
==0,解得m=,
又抛物线有最低点,图象开口向上,∴m﹣1>0,即m>1,
∴m=.
14.二次函数y=ax2﹣4x﹣13a有最小值﹣17,则a= 1或 .
解:∵二次函数y=ax2﹣4x﹣13a有最小值﹣17,∴a>0,
y最小值===﹣13a2﹣4=﹣17,解得a=1或,
均合题意.
15.如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 ﹣2+2 .
解:把A(2,4)代入y=ax2中得4=4a,解得a=1,∴y=x2,
设点C横坐标为m,则CD=CE=2m,∴点E坐标为(m,4﹣2m),∴m2=4﹣2m,
解得m=﹣1﹣(舍)或m=﹣1+.∴CD=2m=﹣2+2.
故答案为:﹣2+2.
16.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
下列结论:①a>0;②当x<﹣2时,y的值随x的增大而减小;
③方程ax2+bx+c=﹣5有两个不相等的实数根.④当x=﹣2时,函数有最小值﹣6.其中,正确结论的序号是 ①②③ (把所有正确结论的序号都填上).
解:将(﹣4,0)、(0,﹣4)、(2,6)代入二次函数y=ax2+bx+c中,得:
,解得:,
故此二次函数解析式为y=x2+3x﹣4,∴a>0,①正确;
对称轴为x=,当x=函数值最小,④错误;
当x<时,y随x的增大而减小,故x<﹣2时,y的值随x的增大而减小,②正确;
令x2+3x﹣4=﹣5,整理得:x2+3x+1=0,Δ=b2﹣4ac=9﹣4=5>0,
故方程ax2+bx+c=﹣5有两个不相等的实数根,③正确.
故正确序号有:①②③,故答案为:①②③.
三.解答题
17.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.
解:∵函数的最大值是2,则此函数顶点的纵坐标是2,
又顶点在y=x+1上,那么顶点的横坐标是1,
设此函数的解析式是y=a(x﹣1)2+2,
再把(2,1)代入函数中可得
a(2﹣1)2+2=1,
解得a=﹣1,
故函数解析式是y=﹣x2+2x+1.
18.已知:在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
解:如图,设HG=x,PD=y,
∵四边形EFGH是矩形,
∴HG∥EF,
∴△AHG∽△ABC,
∴=,
∵BC=20,AD=16,
∴=,
解得y=﹣x+16,
∴矩形EFGH的面积=xy=x(﹣x+16)=﹣(x﹣10)2+80,
∴当x=10,即HG=10时,内接矩形EFGH有最大面积,最大面积是80.
19.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 4 个.
解:(1)∵点A、B在y=x2的图象上,A、B的横坐标分别为﹣2、4,
∴A(﹣2,1),B(4,4),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=+2;
(2)在y=+2中,令x=0,则y=2,
∴C的坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=+=6.
(3)过OC的中点,作AB的平行线交抛物线两个交点P1、P2,此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,
作直线P1P2关于直线AB的对称直线,交抛物线两个交点P3、P4,此时△P3AB的面积和△P4AB的面积等于△AOB的面积的一半,
所以这样的点P共有4个,
故答案为4.
一.选择题
1.如果y=(m﹣2)是关于x的二次函数,则m=( )
A.﹣1 B.2 C.﹣1或2 D.m不存在
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
4.二次函数y=﹣x2﹣2x+1图象的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线y=x2﹣x﹣6与x轴的交点坐标是( )
A.(3,0) B.(﹣2,0)
C.(﹣6,0),(1,0) D.(3,0),(﹣2,0)
6.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
7.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
A. B. C. D.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
9.如图,对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,a≠0),则下列结论:①abc>0,②b2>4ac,③4a+2b+c<0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x>0时,y随x的增大而增大,正确的个数为( )
A.2 B.3 C.4 D.5
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )
A.5 B. C.4 D.
二.填空题
11.抛物线y=x2﹣2x+4的顶点坐标是 ,对称轴为 .
12.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0<x<2时,y关于x的函数解析式为 .
13.若抛物线y=(m﹣1)x2+2mx+2m﹣1的图象的最低点的纵坐标为零,则m= .
14.二次函数y=ax2﹣4x﹣13a有最小值﹣17,则a= .
15.如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
16.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
下列结论:①a>0;②当x<﹣2时,y的值随x的增大而减小;③方程ax2+bx+c=﹣5有两个不相等的实数根.④当x=﹣2时,函数有最小值﹣6.
其中,正确结论的序号是 (把所有正确结论的序号都填上).
三.解答题
17.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.
18.已知:在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
19.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
二次函数图像与性质综合检测题答案提示
一.选择题
1.如果y=(m﹣2)是关于x的二次函数,则m=( )
A.﹣1 B.2 C.﹣1或2 D.m不存在
解:令m2﹣m=2,解得m=2或m=﹣1,且m﹣2≠0,m≠2,因此m=﹣1,
故选:A.
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
解:因为抛物线y=x2向上平移2个单位,得到y=x2+2,
所以,开口方向相同;形状完全相同;对称轴相同.
正确的有三个,故选D.
3.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
解:如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
故选:B.
4.二次函数y=﹣x2﹣2x+1图象的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:∵y=﹣x2﹣2x+1=﹣(x2+2x+1﹣1)+1=﹣(x+1)2+2,
∴顶点坐标为(﹣1,2),∴顶点在第二象限,
故选:B.
5.抛物线y=x2﹣x﹣6与x轴的交点坐标是( )
A.(3,0) B.(﹣2,0)
C.(﹣6,0),(1,0) D.(3,0),(﹣2,0)
解:令y=0,求出x的值为﹣2与3,故交点坐标为(3,0),(﹣2,0),
故选:D.
6.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A. B.4 C.﹣ D.﹣
解:∵点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,∴a=0,∴n=m2+4,∴m﹣n=m﹣(m2+4)=﹣m2+m﹣4=﹣(m﹣)2﹣,
∴当m=时,m﹣n取得最大值,此时m﹣n=﹣,
故选:C.
7.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
A. B. C. D.
解:A、由一次函数y=ax+c图象,得a>0,c<0,由二次函数y=ax2+bx+c图象,得a<0,c>0,故A错误;
B、由一次函数y=ax+c图象,得a>0,c>0,由二次函数y=ax2+bx+c图象,得a>0,c<0,故B错误;
C、由一次函数y=ax+c图象,得a<0,c>0,由二次函数y=ax2+bx+c图象,得a<0,c>0,故C正确;
D、由一次函数y=ax+c图象,得a<0,c>0,由二次函数y=ax2+bx+c图象,得a>0,c>0,故D错误;
故选:C.
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
解:①∵由抛物线的开口向上知a>0,∵对称轴位于y轴的右侧,∴b<0.
∵抛物线与y轴交于负半轴,∴c<0,∴abc>0;故错误;
②对称轴为直线x=﹣<1,得2a>﹣b,即2a+b>0,故错误;
③如图,当x=﹣2时,y>0,4a﹣2b+c>0,故正确;
④∵当x=﹣1时,y=0,∴0=a﹣b+c<a+2a+c=3a+c,即3a+c>0.故正确.
综上所述,有2个结论正确.故选:B.
9.如图,对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,a≠0),则下列结论:①abc>0,②b2>4ac,③4a+2b+c<0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x>0时,y随x的增大而增大,正确的个数为( )
A.2 B.3 C.4 D.5
解:①由图象可知:a>0,c<0,∵﹣=1,∴b=﹣2a<0,∴abc>0,故①正确;
②∵抛物线与x轴有两个交点,∴b2﹣4ac>0,∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③正确;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,∴3a+c>0,故④正确;
⑤当x=1时,y取到值最小,此时,y=a+b+c,而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,故a+b≤am2+bm,即a+b≤m(am+b),故⑤正确,
⑥当x>0时,y先随x的增大而减小,故⑥错误,故选:D.
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )
A.5 B. C.4 D.
解:如图,由题意可得,互异二次函数y=(x﹣m)2﹣m的顶点(m,﹣m)在直线y=﹣x上运动,
在正方形OABC中,点A(0,2),点C(2,0),
∴B(2,2),
从图象可以看出,当函数图象从左上向右下运动时,若抛物线与正方形有交点,先经过点A,再逐渐经过点O,点B,点C,最后再经过点B,且在运动的过程中,两次经过点A,两次经过点O,点B和点C,
∴只需算出当函数经过点A及点B时m的值,即可求出m的最大值及最小值.
当互异二次函数y=(x﹣m)2﹣m经过点A(0,2)时,m=2或m=﹣1;
当互异二次函数y=(x﹣m)2﹣m经过点B(2,2)时,m=或m=.
∴互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值分别是,﹣1.
∴最大值和最小值之差为﹣(﹣1)=,
故选:B.
二.填空题
11.抛物线y=x2﹣2x+4的顶点坐标是 (1,3) ,对称轴为 直线x=1 .
解:y=x2﹣2x+4=(x﹣1)2+3,
所以抛物线y=x2﹣2x+4的顶点坐标是(1,3),对称轴是直线x=1,
故答案为:(1,3),直线x=1.
12.如图,在正方形ABCD中,AB=2,点E在边BC上,点F在边AD的延长线上,AF=EF,设BE=x,AF=y,当0<x<2时,y关于x的函数解析式为 y=(0<x<2) .
解:过点F作FM⊥AE,垂足为M,∵AF=EF,∴AM=ME,
在Rt△ABE中,AE==,∴AM=,
∵∠B=∠AMF=90°,∠FAM=∠AEB,∴△ABE∽△FMA,
∴=,即=,∴xy=,
即y=(0<x<2),故答案为:y=(0<x<2).
13.若抛物线y=(m﹣1)x2+2mx+2m﹣1的图象的最低点的纵坐标为零,则m= .
解:根据题意,根据函数的顶点的坐标公式得,
==0,解得m=,
又抛物线有最低点,图象开口向上,∴m﹣1>0,即m>1,
∴m=.
14.二次函数y=ax2﹣4x﹣13a有最小值﹣17,则a= 1或 .
解:∵二次函数y=ax2﹣4x﹣13a有最小值﹣17,∴a>0,
y最小值===﹣13a2﹣4=﹣17,解得a=1或,
均合题意.
15.如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 ﹣2+2 .
解:把A(2,4)代入y=ax2中得4=4a,解得a=1,∴y=x2,
设点C横坐标为m,则CD=CE=2m,∴点E坐标为(m,4﹣2m),∴m2=4﹣2m,
解得m=﹣1﹣(舍)或m=﹣1+.∴CD=2m=﹣2+2.
故答案为:﹣2+2.
16.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:
x ﹣5 ﹣4 ﹣2 0 2
y 6 0 ﹣6 ﹣4 6
下列结论:①a>0;②当x<﹣2时,y的值随x的增大而减小;
③方程ax2+bx+c=﹣5有两个不相等的实数根.④当x=﹣2时,函数有最小值﹣6.其中,正确结论的序号是 ①②③ (把所有正确结论的序号都填上).
解:将(﹣4,0)、(0,﹣4)、(2,6)代入二次函数y=ax2+bx+c中,得:
,解得:,
故此二次函数解析式为y=x2+3x﹣4,∴a>0,①正确;
对称轴为x=,当x=函数值最小,④错误;
当x<时,y随x的增大而减小,故x<﹣2时,y的值随x的增大而减小,②正确;
令x2+3x﹣4=﹣5,整理得:x2+3x+1=0,Δ=b2﹣4ac=9﹣4=5>0,
故方程ax2+bx+c=﹣5有两个不相等的实数根,③正确.
故正确序号有:①②③,故答案为:①②③.
三.解答题
17.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.
解:∵函数的最大值是2,则此函数顶点的纵坐标是2,
又顶点在y=x+1上,那么顶点的横坐标是1,
设此函数的解析式是y=a(x﹣1)2+2,
再把(2,1)代入函数中可得
a(2﹣1)2+2=1,
解得a=﹣1,
故函数解析式是y=﹣x2+2x+1.
18.已知:在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
解:如图,设HG=x,PD=y,
∵四边形EFGH是矩形,
∴HG∥EF,
∴△AHG∽△ABC,
∴=,
∵BC=20,AD=16,
∴=,
解得y=﹣x+16,
∴矩形EFGH的面积=xy=x(﹣x+16)=﹣(x﹣10)2+80,
∴当x=10,即HG=10时,内接矩形EFGH有最大面积,最大面积是80.
19.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 4 个.
解:(1)∵点A、B在y=x2的图象上,A、B的横坐标分别为﹣2、4,
∴A(﹣2,1),B(4,4),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=+2;
(2)在y=+2中,令x=0,则y=2,
∴C的坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=+=6.
(3)过OC的中点,作AB的平行线交抛物线两个交点P1、P2,此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,
作直线P1P2关于直线AB的对称直线,交抛物线两个交点P3、P4,此时△P3AB的面积和△P4AB的面积等于△AOB的面积的一半,
所以这样的点P共有4个,
故答案为4.
