八年级数学《13.1 平方根》课件
文档属性
| 名称 | 八年级数学《13.1 平方根》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 22:44:43 | ||
图片预览










文档简介
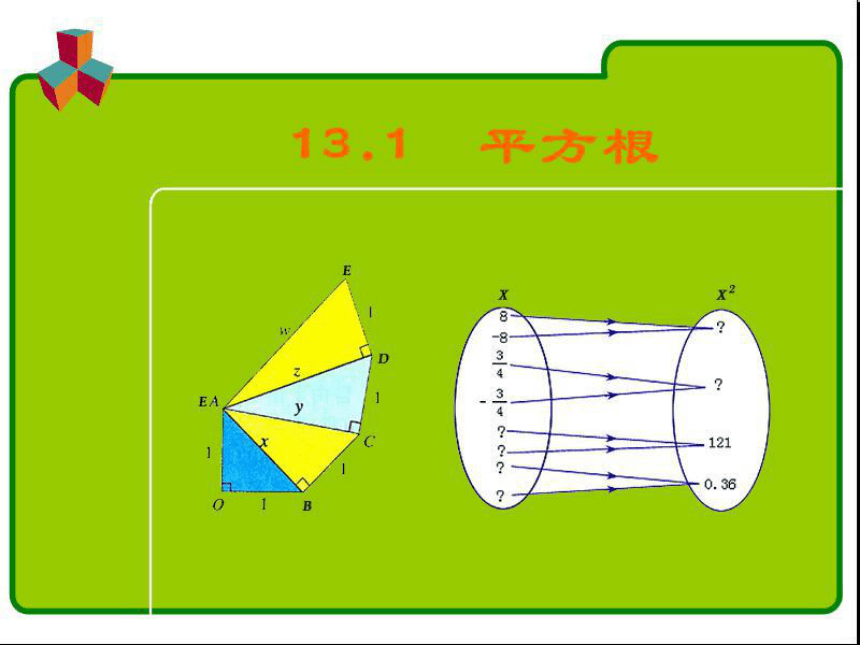
课件49张PPT。13.1 平方根 某教学模具厂要制面积如下表所示的正方形模具,你能帮他们计算出这些正方形模具的边长是多少吗?13 461.41.55 这些正方形模具的边长和面积是什么关系呢?新课导入 1.理解平方根和算术平方根的概念,了解平方与开平方的关系;
2.学会平方根、算术平方根的表示方法;
3.会用计算器求一个数的算术平方根;
4.理解无限不循环的含义,能用夹值法估计一个数的算术平方根的大小范围;
5.理解被开方数越大,它的算术平方根也越大,被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律.教学目标知识与能力 1.发展数感,经历认识平方根的概念,经历总结发现正数、负数、零的平方根的情况;
2.会求一个数的平方根;
3.理解开平方与平方互为逆运算;
4.通过学习算数平方根,建立初步的数感和符号感,发展抽象思维; 5.通过探究 的大小,培养估算意识,了解从两个方向无限逼近的数学思想.过程与方法 1.通过学习算术平方根,进一步建立数感和符号感,发展抽象思维;
2.通过探究被开方数扩大(缩小)与它的算术平方根扩大(缩小)的规律,培养观察能力,抽象概括能力;
3.培养优算意识,了解两个方向无限逼近的数学思想;情感态度与价值观 4.体验“无限不循环”的含义,感受存在着不同于有理数的一类新数;
5.通过用计算器求值及近似值计算,提高运算能力和动手能力;
6.通过利用计算器求值体验现代科技产品迅速、精确的功能,激发学习知识的兴趣. 1.平方根的概念、算术平方根的定义; 2.探索被开方数扩大(缩小)与算术平方根扩大(缩小)的规律;
3.用计算器求一个正数的平方根的程序 ;
4.体验“无限不循环”的含义.教学重难点重点 1.平方根的概念和平方根的表示方法;
2.利用平方根定义解决问题;
3.用夹值法估计一个(无理)数的大小;
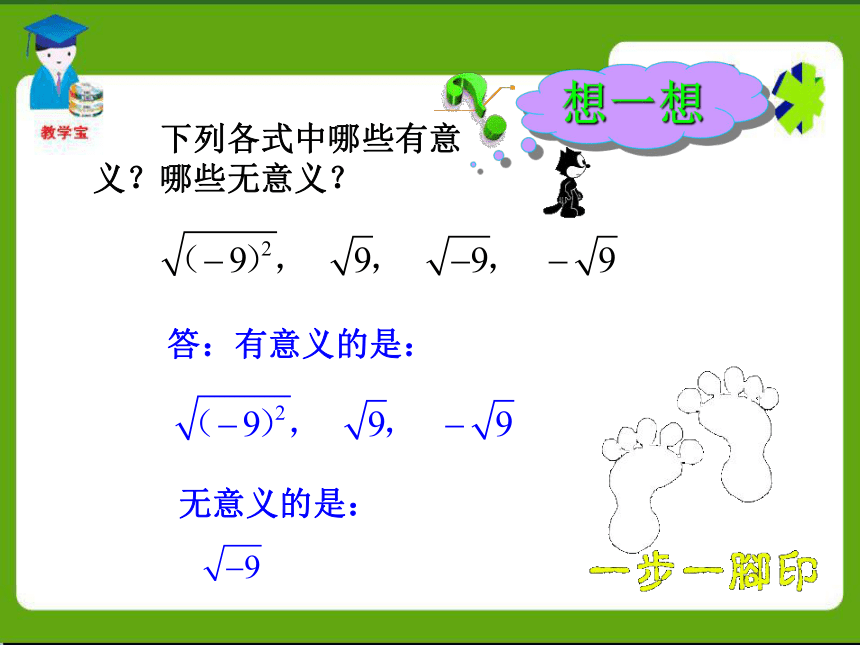
4.准确用计算器求解一个正数的平方根.难点知识要点规定:0的算术平方根是0. 一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.a的算术平方根记为 ,读作“根号a”,a叫做被开方数. 是算术平方根的运算符号.a的算术平方根也是非负数,即 . 其中:表示a的算术平方根.被开方数a是非负数,即a≥0. 下列各式中哪些有意义?哪些无意义?答:有意义的是:无意义的是:想一想例1 求下列各数的算术平方根:
(1)400 (2) (3)0.0025 解:(1)因为202=400,所以400的算术平方根为20,即 =20. (3)因为0.052=0.0025,所以0.0025的算术平方根为0.05,即 =0.01. (2)因为 = ,所以 的算术平方根
是 ,即 = .例2 填空
(1)121 的算术平方根是______;
0.25 的算术平方根是_______;
0 的算术平方根是_______.
(2)100 的算术平方根是______;
25 的算术平方根是_______;
0.81 的算术平方根是_______.00.9510110.5比较结果:1 < 4 < 9 < 16 < 25<36,被开方数大的数算术平方根也大.解: 例3 求下列各数的算术平方根,并用“ < ” 分别把被开方数和算术平方根连接起来.
1,4,9,16,25.36结论 解:设这个正方形原来的边长为a,则其原来的面积为a2.又设变大后的正方形的边长为b,则
b2=4a2=(2a)2 所以,正方形的面积变为原来的4倍,则其边长变为原来的2倍. 例4 一个正方形的面积变为原来的4倍,其边长变为原来的多少倍?正方形的面积扩大n倍,那么其边长对应扩大 倍.结论 某气垫厂接到订单,要求把两块面积为1的正方形材料,缝成一块正方形的气垫面,你有没有办法进行设计,帮助他们解决这个问题?缝成的这个大正方形的边长是多少呢?想一想 如图,把两个小正方形材料沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形气垫面.小正方形的对角线长度即为大正方形的边长. 设大正方形的边长为x,则
x2=2.
由算术平方根的意义可知
x= . 有多大呢? 接着往下计算,可以发现 =1.414 213 56…,是一个无限不循环小数.想一想∵12=1,22=4,
∴1< <2;
∵1.42=1.96,1.52=2.25,
∴1.4< <1.5;
∵1.412=1.999 396,1.4152=2.002 225,
∴1.414< <1.415
…… 第一个发现这样数的人是希伯索斯,但他却被抛进了大海,你想知道这其中的曲折离奇吗?
这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理.无限不循环小数的发现读一读 毕达哥拉斯认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述. 但后来,这学派的一位年轻成员希伯索斯发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海. 无限不循环小数的计算:借助于计算器. 无限不循环小数:即无理数,是指小数位数无限,且小数部分不循环的小数.
无限不循环小数是不能转化为分数的. 常见无限不循环小数:圆周率π,自然对数的底数e, ……知识要点 例5 用计算器求下列各式的值(精确到0.01):解: 例6 用计算器计算下列各数的值,有什么规律? 规律:被开方数扩大(缩小)100倍,它的算术平方根扩大(缩小)10倍.解:结论 能用一块面积为100cm2的正方形纸片沿着边的方向裁出一块面积为90cm2的长方形纸片,使它的长宽之比为3:2吗?想一想 解:设长方形纸片的长为3x cm,宽为2x cm.根据边长与面积的关系得 答:不能用这块正方形纸片裁出符合要求的长方形纸片.因此长方形的长应为 cm. 因为15>12.25,所以 >3.5.
所以 >10.5,所以长方形纸片的长大于原正方形的长(10cm ). 宇宙飞船离开地球进入轨道正常运行的速度v(米/秒)要大于第一宇宙速度v1(米/秒),小于第二宇宙速度v2(米/秒),其中v12=gR,v22=2gR,g≈9.8米/秒2,R≈ 6400000米(地球半径),求v的范围.练一练所以7900 根据乘方运算,可知42=16cm2.想一想16cm2 我们知道,(±4)2=16,但-4不符合题意.
所以,方桌面的边长应是4cm. 反过来,要做一张面积是16cm2的桌面,它的边长是多少cm?知识要点 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,即如果x2=a,那么x叫做a的平方根. 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根.平方与开平方互为逆运算.平方根的表示法: 一个非负数a的平方根用符号表示为:± ,
读作:“正、负根号a”,其中a叫做被开方数.即:如果x2=a,则x=± . 注意 (1) 表示非负数a的正的平方根,即算数平方根,
- 表示非负数a的负的平方根;
(2)± 表示非负数a的平方根,
与- 互为相反数;
(3) 在± 中,a≥0.(4)( )2=a (a≥0), (5)一个正数有两个平方根,它们互为相反数.
零的平方根是零.
负数没有平方根.区别:
1.定义不同; 2.个数不同;
3.表示法不同; 4.取值范围不同.平方根与算术平方根的联系与区别:联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.例7 求下列各数的平方根:
(1)25;(2)81;(3)0.16;(4)121. 解:(1)因为(±5)2=25,所以25的平方根是±5;
(2)因为(±9)2=81,所以81的平方根是±9;
(3)因为(±0.4)2=0.16,所以0.16的平方根是±0.4;
(4)因为(±11)2=121,所以121的平方根是±11. 已知一个自然数的算术平方根是n,则与这个自然数相邻的下一个自然数的平方根是多少? 解:因为这个数的算术平方根是n,所以这个自然数为n2,那么与它相邻的下一个自然数为n2+1.
所以下一个自然数的平方根是 .想一想 已知a+6与2a-9是m的平方根,试求m的值. 解:因为a+6与2a-9是m的平方根,则a+6与2a-9相等或互为相反数.
当 a+6=2a-9时,得a=15.
所以m=152=225.
当a+6+2a-9=0时,得a=1,所以m=1.
所以,m的值为225或1.练一练 一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.正数a的算术平方根记作: . 1.算数平方根0的算术平方根还是0.课堂小结2.平方根 一个数的平方等于a,这个数叫做a的平方根.性质: 一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.平方根的表示法: .3.无理数 即无限不循环小数.无理数不能写成分数的形式.1.(-8)2的平方根是____,算术平方根是____;±882. 的平方根是_____,算术平方 根是____;±333.若x2=49,则 x=____,若 =9,则x=_____;±74.若(x-2)2=36,则x=__________;±98或-4随堂练习5.对于正数a, 等于___;a7.下列各数中,不一定有平方根的是( )
A.2x2+5 B.|x|+2
C. D.|a|-26.对于任意数a, 等于______________
___________________________________
____________. 若a是正数,则等于a;若a是负数,则等于-a;若a是0,则等于0DD8.已知 有意义,则下列说法正确的是( )
A.一定是正数 B.x一定是负数
C.x一定是非负数 D.x一定是非正数 9.已知(2x)2=36,y是(-5)2的正的平方根,求代数 式5x-3y的值.10.一个数的两个平方根分别是 3a+2 与
5a-10,求这个数. 解:因为一个数的平方根互为相反数,
所以,
(3a+2)+(5a-10)=0
所以 a=1.习题答案5.(1)29.44;(2)0.68;(3)-0.57;
(4)±49.01.
6.6和7.
7.(1)±16.4;(2)16.9;(3)在16.4与
16.5之间;(4)16.1.
8.(1)±5;(2)±9;(3)± .
9.5s.
10.2倍,3倍, 倍.
11.(1)2,3,5,6,7,0;a(a≥0),
-a(a<0). (2)4,9,25,36,49,0;a.
12.1不断开平方的结果仍为1;对于小于1的
正数,每次开平方的结果逐渐增大,并
趋近于1;对于大于1的数,每次开平方
的结果逐渐减小,并趋近于1.
2.学会平方根、算术平方根的表示方法;
3.会用计算器求一个数的算术平方根;
4.理解无限不循环的含义,能用夹值法估计一个数的算术平方根的大小范围;
5.理解被开方数越大,它的算术平方根也越大,被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律.教学目标知识与能力 1.发展数感,经历认识平方根的概念,经历总结发现正数、负数、零的平方根的情况;
2.会求一个数的平方根;
3.理解开平方与平方互为逆运算;
4.通过学习算数平方根,建立初步的数感和符号感,发展抽象思维; 5.通过探究 的大小,培养估算意识,了解从两个方向无限逼近的数学思想.过程与方法 1.通过学习算术平方根,进一步建立数感和符号感,发展抽象思维;
2.通过探究被开方数扩大(缩小)与它的算术平方根扩大(缩小)的规律,培养观察能力,抽象概括能力;
3.培养优算意识,了解两个方向无限逼近的数学思想;情感态度与价值观 4.体验“无限不循环”的含义,感受存在着不同于有理数的一类新数;
5.通过用计算器求值及近似值计算,提高运算能力和动手能力;
6.通过利用计算器求值体验现代科技产品迅速、精确的功能,激发学习知识的兴趣. 1.平方根的概念、算术平方根的定义; 2.探索被开方数扩大(缩小)与算术平方根扩大(缩小)的规律;
3.用计算器求一个正数的平方根的程序 ;
4.体验“无限不循环”的含义.教学重难点重点 1.平方根的概念和平方根的表示方法;
2.利用平方根定义解决问题;
3.用夹值法估计一个(无理)数的大小;
4.准确用计算器求解一个正数的平方根.难点知识要点规定:0的算术平方根是0. 一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.a的算术平方根记为 ,读作“根号a”,a叫做被开方数. 是算术平方根的运算符号.a的算术平方根也是非负数,即 . 其中:表示a的算术平方根.被开方数a是非负数,即a≥0. 下列各式中哪些有意义?哪些无意义?答:有意义的是:无意义的是:想一想例1 求下列各数的算术平方根:
(1)400 (2) (3)0.0025 解:(1)因为202=400,所以400的算术平方根为20,即 =20. (3)因为0.052=0.0025,所以0.0025的算术平方根为0.05,即 =0.01. (2)因为 = ,所以 的算术平方根
是 ,即 = .例2 填空
(1)121 的算术平方根是______;
0.25 的算术平方根是_______;
0 的算术平方根是_______.
(2)100 的算术平方根是______;
25 的算术平方根是_______;
0.81 的算术平方根是_______.00.9510110.5比较结果:1 < 4 < 9 < 16 < 25<36,被开方数大的数算术平方根也大.解: 例3 求下列各数的算术平方根,并用“ < ” 分别把被开方数和算术平方根连接起来.
1,4,9,16,25.36结论 解:设这个正方形原来的边长为a,则其原来的面积为a2.又设变大后的正方形的边长为b,则
b2=4a2=(2a)2 所以,正方形的面积变为原来的4倍,则其边长变为原来的2倍. 例4 一个正方形的面积变为原来的4倍,其边长变为原来的多少倍?正方形的面积扩大n倍,那么其边长对应扩大 倍.结论 某气垫厂接到订单,要求把两块面积为1的正方形材料,缝成一块正方形的气垫面,你有没有办法进行设计,帮助他们解决这个问题?缝成的这个大正方形的边长是多少呢?想一想 如图,把两个小正方形材料沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形气垫面.小正方形的对角线长度即为大正方形的边长. 设大正方形的边长为x,则
x2=2.
由算术平方根的意义可知
x= . 有多大呢? 接着往下计算,可以发现 =1.414 213 56…,是一个无限不循环小数.想一想∵12=1,22=4,
∴1< <2;
∵1.42=1.96,1.52=2.25,
∴1.4< <1.5;
∵1.412=1.999 396,1.4152=2.002 225,
∴1.414< <1.415
…… 第一个发现这样数的人是希伯索斯,但他却被抛进了大海,你想知道这其中的曲折离奇吗?
这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理.无限不循环小数的发现读一读 毕达哥拉斯认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述. 但后来,这学派的一位年轻成员希伯索斯发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海. 无限不循环小数的计算:借助于计算器. 无限不循环小数:即无理数,是指小数位数无限,且小数部分不循环的小数.
无限不循环小数是不能转化为分数的. 常见无限不循环小数:圆周率π,自然对数的底数e, ……知识要点 例5 用计算器求下列各式的值(精确到0.01):解: 例6 用计算器计算下列各数的值,有什么规律? 规律:被开方数扩大(缩小)100倍,它的算术平方根扩大(缩小)10倍.解:结论 能用一块面积为100cm2的正方形纸片沿着边的方向裁出一块面积为90cm2的长方形纸片,使它的长宽之比为3:2吗?想一想 解:设长方形纸片的长为3x cm,宽为2x cm.根据边长与面积的关系得 答:不能用这块正方形纸片裁出符合要求的长方形纸片.因此长方形的长应为 cm. 因为15>12.25,所以 >3.5.
所以 >10.5,所以长方形纸片的长大于原正方形的长(10cm ). 宇宙飞船离开地球进入轨道正常运行的速度v(米/秒)要大于第一宇宙速度v1(米/秒),小于第二宇宙速度v2(米/秒),其中v12=gR,v22=2gR,g≈9.8米/秒2,R≈ 6400000米(地球半径),求v的范围.练一练所以7900
所以,方桌面的边长应是4cm. 反过来,要做一张面积是16cm2的桌面,它的边长是多少cm?知识要点 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,即如果x2=a,那么x叫做a的平方根. 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根.平方与开平方互为逆运算.平方根的表示法: 一个非负数a的平方根用符号表示为:± ,
读作:“正、负根号a”,其中a叫做被开方数.即:如果x2=a,则x=± . 注意 (1) 表示非负数a的正的平方根,即算数平方根,
- 表示非负数a的负的平方根;
(2)± 表示非负数a的平方根,
与- 互为相反数;
(3) 在± 中,a≥0.(4)( )2=a (a≥0), (5)一个正数有两个平方根,它们互为相反数.
零的平方根是零.
负数没有平方根.区别:
1.定义不同; 2.个数不同;
3.表示法不同; 4.取值范围不同.平方根与算术平方根的联系与区别:联系:
1.算术平方根是平方根的一种;
2.只有非负数才有算术平方根和平方根;
3.0的算术平方根和平方根都是0.例7 求下列各数的平方根:
(1)25;(2)81;(3)0.16;(4)121. 解:(1)因为(±5)2=25,所以25的平方根是±5;
(2)因为(±9)2=81,所以81的平方根是±9;
(3)因为(±0.4)2=0.16,所以0.16的平方根是±0.4;
(4)因为(±11)2=121,所以121的平方根是±11. 已知一个自然数的算术平方根是n,则与这个自然数相邻的下一个自然数的平方根是多少? 解:因为这个数的算术平方根是n,所以这个自然数为n2,那么与它相邻的下一个自然数为n2+1.
所以下一个自然数的平方根是 .想一想 已知a+6与2a-9是m的平方根,试求m的值. 解:因为a+6与2a-9是m的平方根,则a+6与2a-9相等或互为相反数.
当 a+6=2a-9时,得a=15.
所以m=152=225.
当a+6+2a-9=0时,得a=1,所以m=1.
所以,m的值为225或1.练一练 一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.正数a的算术平方根记作: . 1.算数平方根0的算术平方根还是0.课堂小结2.平方根 一个数的平方等于a,这个数叫做a的平方根.性质: 一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.平方根的表示法: .3.无理数 即无限不循环小数.无理数不能写成分数的形式.1.(-8)2的平方根是____,算术平方根是____;±882. 的平方根是_____,算术平方 根是____;±333.若x2=49,则 x=____,若 =9,则x=_____;±74.若(x-2)2=36,则x=__________;±98或-4随堂练习5.对于正数a, 等于___;a7.下列各数中,不一定有平方根的是( )
A.2x2+5 B.|x|+2
C. D.|a|-26.对于任意数a, 等于______________
___________________________________
____________. 若a是正数,则等于a;若a是负数,则等于-a;若a是0,则等于0DD8.已知 有意义,则下列说法正确的是( )
A.一定是正数 B.x一定是负数
C.x一定是非负数 D.x一定是非正数 9.已知(2x)2=36,y是(-5)2的正的平方根,求代数 式5x-3y的值.10.一个数的两个平方根分别是 3a+2 与
5a-10,求这个数. 解:因为一个数的平方根互为相反数,
所以,
(3a+2)+(5a-10)=0
所以 a=1.习题答案5.(1)29.44;(2)0.68;(3)-0.57;
(4)±49.01.
6.6和7.
7.(1)±16.4;(2)16.9;(3)在16.4与
16.5之间;(4)16.1.
8.(1)±5;(2)±9;(3)± .
9.5s.
10.2倍,3倍, 倍.
11.(1)2,3,5,6,7,0;a(a≥0),
-a(a<0). (2)4,9,25,36,49,0;a.
12.1不断开平方的结果仍为1;对于小于1的
正数,每次开平方的结果逐渐增大,并
趋近于1;对于大于1的数,每次开平方
的结果逐渐减小,并趋近于1.
