北师大版八下数学6.3三角形的中位线--中点四边形课件(17张ppt)
文档属性
| 名称 | 北师大版八下数学6.3三角形的中位线--中点四边形课件(17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 11:19:29 | ||
图片预览





文档简介
(共17张PPT)
中点四边形
顺次连结任意四边形的各边中点所组成的四边形( )
C
A
D
B
猜想:是平行四边形
E
H
G
F
简称:中点四边形
你知道它是什么四边形?能证明你的猜想吗?
A
D
B
C
H
G
F
E
证明:连接BD
∵ E,H是△ABD的两边中点
∴ EH∥BD,且EH= BD
同理:FG ∥BD,且FG= BD
EH∥FG,且EF=FG
∴ 四边形EFGH是平行四边形
1
2
1
2
任意四边形中点连线所得的四边形为平行四边形
(1)一个平行四边形;
(3)一个菱形;
(4)一个正方形;
(5)一个等腰梯形;
(6)一个对角线相等的四边形;
(7)一个对角线互相垂直的四边形;
(8)一个对角线相等且互相垂直的四边形。
(2)一个矩形
当原四边形ABCD是下列图形时,中点四边形EFGH是什么四边形?
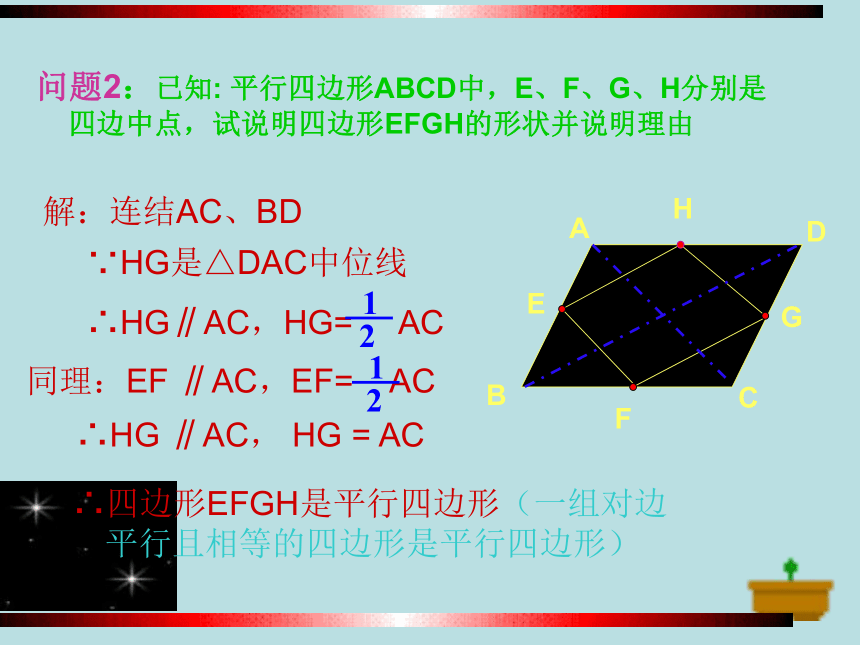
问题2:已知: 平行四边形ABCD中,E、F、G、H分别是四边中点,试说明四边形EFGH的形状并说明理由
B
H
A
C
D
E
F
G
解:连结AC、BD
∵HG是△DAC中位线
∴HG∥AC,HG= AC
同理:EF ∥AC,EF= AC
∴HG ∥AC, HG = AC
∴四边形EFGH是平行四边形(一组对边平行且相等的四边形是平行四边形)
1
2
1
2
问题3:如果四边形ABCD是矩形,则四边形EFGH是什么特殊四边形呢?
A
H
B
C
D
E
F
G
答案:菱形
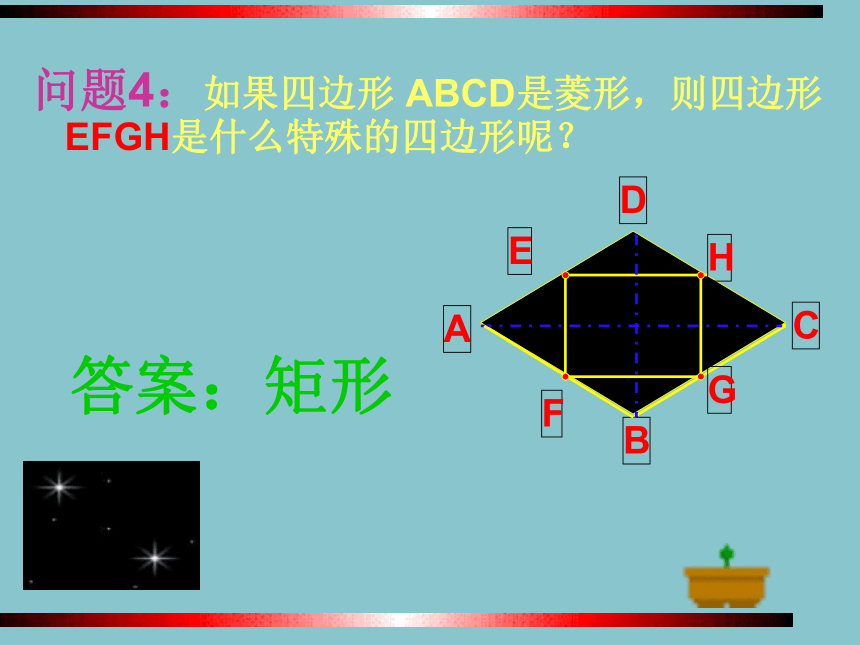
问题4:如果四边形 ABCD是菱形,则四边形EFGH是什么特殊的四边形呢?
A
B
C
D
E
F
G
H
答案:矩形
问题5:如果四边形 ABCD是正方形,则四边形EFGH又是什么特殊四边形?
A
B
C
D
E
F
G
H
答案:正方形
已知:在四边形ABCD中, E、F、G、H分别是四边中点;
(1)如果AC=BD,则
四边形EFGH是 。
(2)如果AC⊥BD,则
四边形EFGH是 。
(3)如果AC=BD、 AC⊥BD,
则四边形EFGH是 。
A
B
C
D
E
F
G
H
菱形
矩形
正方形
结论:
中点四边形的形状与原四边形的对角线有密切关系;
1,如果原四边形的两条对角线相等那么中点四边 形是菱形;
2,如果原四边形的两条对角线互相垂直那么中点四边形是矩形;
3,如果原四边形的两条对角线相等且互相垂直
那么中点四边形是正方形。
反之亦然。
你能用最快的速度回答下列问题吗?
2、等腰梯形的中点四边形是什么图形?
1、梯形的中点四边形是什么图形?
3、梯形的对角线的和是20,则中点四边形的周 长是多少?
答案:平行四边形
答案:菱形
答案:20
如图:在四边形ABCD中,AB=CD,M、N、P、Q分别是AD、BC、BD、AC的中点。求证: MN与PQ互相垂直平分
证明: ∵MP是△ABD的中位线
A
B
C
D
M
N
P
Q
∴MP∥AB,MP= AB
同理:NQ ∥AB,NQ= AB
∴ MP∥NQ,MP=NQ
∴四边形MPNQ是平行四边形
∵MQ是△ADC的中位线
∴MQ=CD
∵AB=CD
∴ MP=MQ
∴四边形MPNQ是菱形
∴MN与PQ互相垂直平分
1
2
1
2
如图13,四边形ABCD中,AC=6,BD=8且AC⊥BD,顺次连接四边形ABCD各边中点,得四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBnCnDn.
(1)说明四边形A1B1C1D1是矩形;
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积.
(3)写出四边形AnBnCnDn的面积;
(4)求四边形A5B5C5D5的周长.
…
A1
A
A2
A3
B
B1
B2
B3
C
C2
C1
C3
D
D2
D1
D3
图13
已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
中点四边形
顺次连结任意四边形的各边中点所组成的四边形( )
C
A
D
B
猜想:是平行四边形
E
H
G
F
简称:中点四边形
你知道它是什么四边形?能证明你的猜想吗?
A
D
B
C
H
G
F
E
证明:连接BD
∵ E,H是△ABD的两边中点
∴ EH∥BD,且EH= BD
同理:FG ∥BD,且FG= BD
EH∥FG,且EF=FG
∴ 四边形EFGH是平行四边形
1
2
1
2
任意四边形中点连线所得的四边形为平行四边形
(1)一个平行四边形;
(3)一个菱形;
(4)一个正方形;
(5)一个等腰梯形;
(6)一个对角线相等的四边形;
(7)一个对角线互相垂直的四边形;
(8)一个对角线相等且互相垂直的四边形。
(2)一个矩形
当原四边形ABCD是下列图形时,中点四边形EFGH是什么四边形?
问题2:已知: 平行四边形ABCD中,E、F、G、H分别是四边中点,试说明四边形EFGH的形状并说明理由
B
H
A
C
D
E
F
G
解:连结AC、BD
∵HG是△DAC中位线
∴HG∥AC,HG= AC
同理:EF ∥AC,EF= AC
∴HG ∥AC, HG = AC
∴四边形EFGH是平行四边形(一组对边平行且相等的四边形是平行四边形)
1
2
1
2
问题3:如果四边形ABCD是矩形,则四边形EFGH是什么特殊四边形呢?
A
H
B
C
D
E
F
G
答案:菱形
问题4:如果四边形 ABCD是菱形,则四边形EFGH是什么特殊的四边形呢?
A
B
C
D
E
F
G
H
答案:矩形
问题5:如果四边形 ABCD是正方形,则四边形EFGH又是什么特殊四边形?
A
B
C
D
E
F
G
H
答案:正方形
已知:在四边形ABCD中, E、F、G、H分别是四边中点;
(1)如果AC=BD,则
四边形EFGH是 。
(2)如果AC⊥BD,则
四边形EFGH是 。
(3)如果AC=BD、 AC⊥BD,
则四边形EFGH是 。
A
B
C
D
E
F
G
H
菱形
矩形
正方形
结论:
中点四边形的形状与原四边形的对角线有密切关系;
1,如果原四边形的两条对角线相等那么中点四边 形是菱形;
2,如果原四边形的两条对角线互相垂直那么中点四边形是矩形;
3,如果原四边形的两条对角线相等且互相垂直
那么中点四边形是正方形。
反之亦然。
你能用最快的速度回答下列问题吗?
2、等腰梯形的中点四边形是什么图形?
1、梯形的中点四边形是什么图形?
3、梯形的对角线的和是20,则中点四边形的周 长是多少?
答案:平行四边形
答案:菱形
答案:20
如图:在四边形ABCD中,AB=CD,M、N、P、Q分别是AD、BC、BD、AC的中点。求证: MN与PQ互相垂直平分
证明: ∵MP是△ABD的中位线
A
B
C
D
M
N
P
Q
∴MP∥AB,MP= AB
同理:NQ ∥AB,NQ= AB
∴ MP∥NQ,MP=NQ
∴四边形MPNQ是平行四边形
∵MQ是△ADC的中位线
∴MQ=CD
∵AB=CD
∴ MP=MQ
∴四边形MPNQ是菱形
∴MN与PQ互相垂直平分
1
2
1
2
如图13,四边形ABCD中,AC=6,BD=8且AC⊥BD,顺次连接四边形ABCD各边中点,得四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去,得到四边形AnBnCnDn.
(1)说明四边形A1B1C1D1是矩形;
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积.
(3)写出四边形AnBnCnDn的面积;
(4)求四边形A5B5C5D5的周长.
…
A1
A
A2
A3
B
B1
B2
B3
C
C2
C1
C3
D
D2
D1
D3
图13
已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
