华东师大版数学九年级上册 25.1 在重复试验中观察不确定现象 第一课时 课件 (共27张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 25.1 在重复试验中观察不确定现象 第一课时 课件 (共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 770.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 12:27:20 | ||
图片预览








文档简介
(共27张PPT)
25.1在重复试验中观察不确定现象
学习目标
1、进一步熟悉收集、整理、描述和分析数据的活动过程。
2、通过动手操作,体会不可能发生、可能发生和必然发生的概念,并能用“不可能”、“可能”和“必然”等词来描述事件发生的情况。
3、主动探索、敢于实践、勇于发现、合作交流。
学习重点
体验必然事件、不可能事件和随机事件的存在于日常生活的方方面面。
学习难点
明确事件发生的可能性是有大有小的。
创设情境 导入新课
2014年3月8日,马航失联,你认为所有乘客和机组人员还有生还的可能性吗?
本学期的期中考试九年级总分第一名和单科第一名都是我们班的吗?
合作交流 探究新知
我们两人一组做一个“掷骰子”的游戏.
游戏用具:每组准备一个普通的正方体骰子,它有六个面,每一面的点数分别是从1到6这6个数字中的一个.骰子质地要均匀,以便使每个数字被掷得的机会均等.游戏中要求一个同学掷骰子,另一个同学做记录,用“正”字法把每个点数出现的频数记录下来,填入下表.掷完20次后,两人交换角色.两位同学的试验数据都记录在下表中:
掷骰子40次骰子上每个数出现的频数频率表
1.不可能事件
请同学们观察表1,“点数7”出现的次数为_______,如果再多掷几次,“掷得的点数是7”这件事会不会发生?
观察所有小组表1中,“点数7”出现的次数总是0.骰子上没有7,所以再多掷几次,“掷得的点数是7”这件事都不会出现的。
师生交流:“掷得的点数是7”这件事是不可能发生的.
“不可能”发生就是指每次都完全没有机会发生,或者说,发生的机会是0.
在每次试验中都一定不会发生的事件为不可能事件
2、必然事件
掷得的点数小于7这件事会不会发生?发生几次? 这件事一定会发生,每次都发生。
师生交流:每次都一定发生,不可能不发生,或者说,发生的机会是100%,我们称之为“必然”发生。
在每次试验中都一定会发生的事件为必然事件
在每次试验中都一定不会发生的事件为不可能事件
在每次试验中都一定会发生的事件为必然事件
这两种事件在试验中是否发生都是我们能够预先
确定的,所以统称为确定事件
3、随机事件
掷得的点数是2这件事会不会发生?是必然发生?还是不可能发生?
这件事有时发生,有时不发生,不是必然发生,也不是不可能发生。
无法预先确定在一次试验中会不会发生事件
我们称它们为随机事件
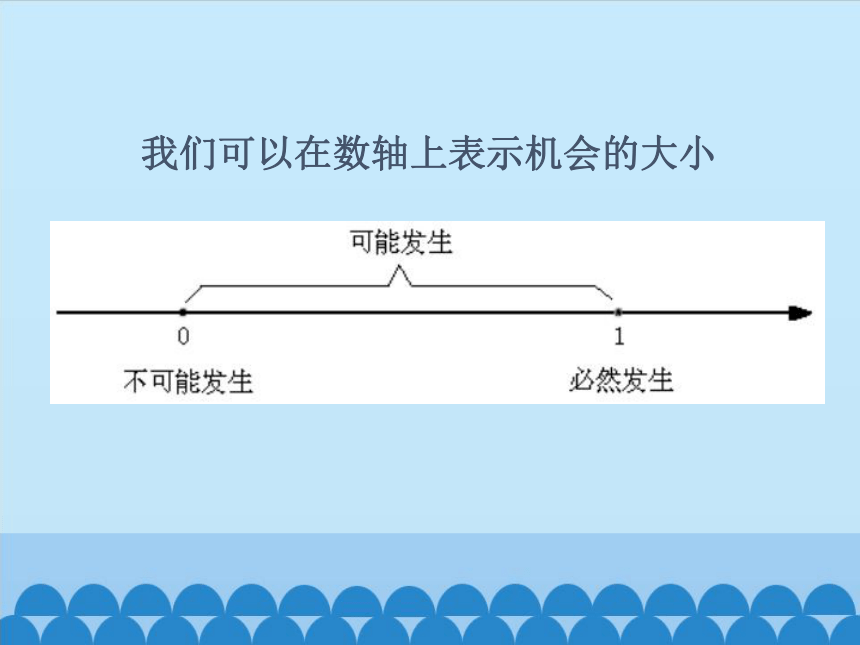
我们可以在数轴上表示机会的大小
确定事件
随机事件
必然事件
不可能事件
例1 指出下列事件是必然事件,不可能事件还是随机事件?
应用新知 体验成功
随机事件
必然事件
必然事件
随机事件
(1)我国东南沿海某地明年将3次受到热带气旋的侵袭;
(2)若a为实数,则|a| 0;
(3)某人开车通过10个路口都将遇到绿灯;
(4)抛一个石头,石头下落;
( 5 ) 一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它抛掷两次,向上的面的数字之和大于12.
( 6 )打开电视机,正在播放新闻
( 7 )在下届亚洲杯上,中国足球队以2:0
战胜日本足球队
随机事件
随机事件
不可能事件
1、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
(1)某地明年1月1日刮西北风;
(2)当x是实数时,
;
(3)手电筒的电池没电,灯泡发亮;
(4)一个电影院某天的上座率超过50%。
随机事件
必然事件
不可能事件
随机事件
(5)从分别标有1,2,3,4,5,6,7,8,9,10的
10张号签中任取一张,得到4号签。
随机事件
达标测试 巩固提高
2、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
① 太阳从东边升起 ;
② 打开电视,它正在播《新闻联播》;
③邵华将夺得100米冠军;
④ 在妇幼保健医院里,下一个出生的婴 儿是女孩;
⑤抛掷1个均匀的骰子,9点朝上;
⑥用力旋转画有红、黄、蓝、绿四色转盘上的指针,指针会停在黑色上。
必然事件
随机事件
不可能事件
随机事件
随机事件
不可能事件
(4)、3天内将下雨;
(2)、1+3>2;
(5)、如果a为有理数,那么|a|<0
(1)、抛掷1个均匀的骰子,6点朝上;
3、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
(3)、打开电视,它正在播广告;
随机事件
随机事件
随机事件
不可能事件
必然事件
跳高运动员最终要落到地面上。
只要功夫深,铁杵磨成针。
电视机不接电源正在播放节目。
“守株待兔”属于什么事件?
买一张彩票就能中一等奖,奖金500万元。
做一做
开心实践站——抽纸片拼原图的游戏:
准备三张大小一样的纸片,上面印有不同图案(如照片、明信片、自己画的图片等),把每张纸片都对折,剪成大小一样的两张,将这六张小纸片有图案的一面朝下,然后混合,让你的同伴随机抽出两张小纸片。
思考:
(1)你认为抽出的那两张小纸片正好能成功拼成原图的机会大吗?
(2)猜一猜,大概是平均几次里会有一次成功呢?
实验目的:研究不确定事件“抽纸片拼成原图”在实验中成功了几次.
实验器具:三张大小一样印有不同图案纸片,一张记录纸,一支笔.
实验步骤:
1、分组:四人一小组,确定一人将图片混合均匀、一人抽
纸,拼图、一人记录、一人监督,四人各施其职。
2、收集数据:每小组各抽取20次,每次任意抽出两张,如
果抽取的两张拼成原图,实验成功,否则失败。并将数据填入
表格中。每完成一次 ,负责将图片混合均匀的同学一定要重
新背着抽图的同学再次混合均匀一次 ,这个步骤很重要!
3、整理数据:将刚才收集到的数据整理,完成表格中的 各个
项目,完成好的数据交给老师进行汇总处理
最后通过实验我们发现:这个实验成功率大约在20%
现在对这个游戏进行理论分析:假如我在六张小纸片上标注A1、A2、A3、B1、B2、B3。其中A1 、B1能够拼成原图, A2、B2能够拼成原图, A3、 B3能够拼成原图。
第一张抽到A1,最后就可以产生以下结果:
第一张抽到A2,最后就可以产生以下结果:
第一张抽到A3,最后就可以产生以下结果:
第一张抽到B1,最后就可以产生以下结果:
第一张抽到B2,最后就可以产生以下结果:
想一想 “有感而发”
A1A2 A1A3 A1B1 A1B2 A1B3
A2A3 A2B1 A2B2 A2B3
A3B1 A3B2 A3B3
B1B2 B1B3
B2B3
在这个实验中会出现15种情况,其中只有A1B1
A2B2 A3B3会成功也就是
通过实验数据和理论分析我们都可以得到能够拼成原来
图片的成功率为20%
这节课你都学到了哪些内容?
确定事件
随机事件
必然事件
不可能事件
可能发生的事件
0
1
不可能
必然
可能
不太可能
很有可能
谢谢!
25.1在重复试验中观察不确定现象
学习目标
1、进一步熟悉收集、整理、描述和分析数据的活动过程。
2、通过动手操作,体会不可能发生、可能发生和必然发生的概念,并能用“不可能”、“可能”和“必然”等词来描述事件发生的情况。
3、主动探索、敢于实践、勇于发现、合作交流。
学习重点
体验必然事件、不可能事件和随机事件的存在于日常生活的方方面面。
学习难点
明确事件发生的可能性是有大有小的。
创设情境 导入新课
2014年3月8日,马航失联,你认为所有乘客和机组人员还有生还的可能性吗?
本学期的期中考试九年级总分第一名和单科第一名都是我们班的吗?
合作交流 探究新知
我们两人一组做一个“掷骰子”的游戏.
游戏用具:每组准备一个普通的正方体骰子,它有六个面,每一面的点数分别是从1到6这6个数字中的一个.骰子质地要均匀,以便使每个数字被掷得的机会均等.游戏中要求一个同学掷骰子,另一个同学做记录,用“正”字法把每个点数出现的频数记录下来,填入下表.掷完20次后,两人交换角色.两位同学的试验数据都记录在下表中:
掷骰子40次骰子上每个数出现的频数频率表
1.不可能事件
请同学们观察表1,“点数7”出现的次数为_______,如果再多掷几次,“掷得的点数是7”这件事会不会发生?
观察所有小组表1中,“点数7”出现的次数总是0.骰子上没有7,所以再多掷几次,“掷得的点数是7”这件事都不会出现的。
师生交流:“掷得的点数是7”这件事是不可能发生的.
“不可能”发生就是指每次都完全没有机会发生,或者说,发生的机会是0.
在每次试验中都一定不会发生的事件为不可能事件
2、必然事件
掷得的点数小于7这件事会不会发生?发生几次? 这件事一定会发生,每次都发生。
师生交流:每次都一定发生,不可能不发生,或者说,发生的机会是100%,我们称之为“必然”发生。
在每次试验中都一定会发生的事件为必然事件
在每次试验中都一定不会发生的事件为不可能事件
在每次试验中都一定会发生的事件为必然事件
这两种事件在试验中是否发生都是我们能够预先
确定的,所以统称为确定事件
3、随机事件
掷得的点数是2这件事会不会发生?是必然发生?还是不可能发生?
这件事有时发生,有时不发生,不是必然发生,也不是不可能发生。
无法预先确定在一次试验中会不会发生事件
我们称它们为随机事件
我们可以在数轴上表示机会的大小
确定事件
随机事件
必然事件
不可能事件
例1 指出下列事件是必然事件,不可能事件还是随机事件?
应用新知 体验成功
随机事件
必然事件
必然事件
随机事件
(1)我国东南沿海某地明年将3次受到热带气旋的侵袭;
(2)若a为实数,则|a| 0;
(3)某人开车通过10个路口都将遇到绿灯;
(4)抛一个石头,石头下落;
( 5 ) 一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它抛掷两次,向上的面的数字之和大于12.
( 6 )打开电视机,正在播放新闻
( 7 )在下届亚洲杯上,中国足球队以2:0
战胜日本足球队
随机事件
随机事件
不可能事件
1、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
(1)某地明年1月1日刮西北风;
(2)当x是实数时,
;
(3)手电筒的电池没电,灯泡发亮;
(4)一个电影院某天的上座率超过50%。
随机事件
必然事件
不可能事件
随机事件
(5)从分别标有1,2,3,4,5,6,7,8,9,10的
10张号签中任取一张,得到4号签。
随机事件
达标测试 巩固提高
2、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
① 太阳从东边升起 ;
② 打开电视,它正在播《新闻联播》;
③邵华将夺得100米冠军;
④ 在妇幼保健医院里,下一个出生的婴 儿是女孩;
⑤抛掷1个均匀的骰子,9点朝上;
⑥用力旋转画有红、黄、蓝、绿四色转盘上的指针,指针会停在黑色上。
必然事件
随机事件
不可能事件
随机事件
随机事件
不可能事件
(4)、3天内将下雨;
(2)、1+3>2;
(5)、如果a为有理数,那么|a|<0
(1)、抛掷1个均匀的骰子,6点朝上;
3、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件?
(3)、打开电视,它正在播广告;
随机事件
随机事件
随机事件
不可能事件
必然事件
跳高运动员最终要落到地面上。
只要功夫深,铁杵磨成针。
电视机不接电源正在播放节目。
“守株待兔”属于什么事件?
买一张彩票就能中一等奖,奖金500万元。
做一做
开心实践站——抽纸片拼原图的游戏:
准备三张大小一样的纸片,上面印有不同图案(如照片、明信片、自己画的图片等),把每张纸片都对折,剪成大小一样的两张,将这六张小纸片有图案的一面朝下,然后混合,让你的同伴随机抽出两张小纸片。
思考:
(1)你认为抽出的那两张小纸片正好能成功拼成原图的机会大吗?
(2)猜一猜,大概是平均几次里会有一次成功呢?
实验目的:研究不确定事件“抽纸片拼成原图”在实验中成功了几次.
实验器具:三张大小一样印有不同图案纸片,一张记录纸,一支笔.
实验步骤:
1、分组:四人一小组,确定一人将图片混合均匀、一人抽
纸,拼图、一人记录、一人监督,四人各施其职。
2、收集数据:每小组各抽取20次,每次任意抽出两张,如
果抽取的两张拼成原图,实验成功,否则失败。并将数据填入
表格中。每完成一次 ,负责将图片混合均匀的同学一定要重
新背着抽图的同学再次混合均匀一次 ,这个步骤很重要!
3、整理数据:将刚才收集到的数据整理,完成表格中的 各个
项目,完成好的数据交给老师进行汇总处理
最后通过实验我们发现:这个实验成功率大约在20%
现在对这个游戏进行理论分析:假如我在六张小纸片上标注A1、A2、A3、B1、B2、B3。其中A1 、B1能够拼成原图, A2、B2能够拼成原图, A3、 B3能够拼成原图。
第一张抽到A1,最后就可以产生以下结果:
第一张抽到A2,最后就可以产生以下结果:
第一张抽到A3,最后就可以产生以下结果:
第一张抽到B1,最后就可以产生以下结果:
第一张抽到B2,最后就可以产生以下结果:
想一想 “有感而发”
A1A2 A1A3 A1B1 A1B2 A1B3
A2A3 A2B1 A2B2 A2B3
A3B1 A3B2 A3B3
B1B2 B1B3
B2B3
在这个实验中会出现15种情况,其中只有A1B1
A2B2 A3B3会成功也就是
通过实验数据和理论分析我们都可以得到能够拼成原来
图片的成功率为20%
这节课你都学到了哪些内容?
确定事件
随机事件
必然事件
不可能事件
可能发生的事件
0
1
不可能
必然
可能
不太可能
很有可能
谢谢!
