人教版七年级数学上册《1-4-1 第1课时 有理数的乘法法则》教学课件PPT优秀公开课(共23张PPT)
文档属性
| 名称 | 人教版七年级数学上册《1-4-1 第1课时 有理数的乘法法则》教学课件PPT优秀公开课(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 15:02:56 | ||
图片预览







文档简介
(共23张PPT)
第一章 有理数
1.4.1 有理数的乘法法则
人教版 数学 七年级 上册
知识与技能:
经历探索有理数乘法法则过程,掌握有理数的乘法法则,能用法则进 行有理数的乘法.
过程与方法:
经历探索有理数乘法法则的过程,发展学生归纳、猜想、验证等能 力.
情感态度与价值观:
培养学生积极探索精神,感受数学与实际生活的联系. 重点:应用法则正确地进行有理数乘法运算.
难点:两负数相乘,积的符号为正与两负数相加和的符号为负号容易 混淆.
学习目标
问题一:有理数包括哪些数?
问题二:小学已经学过的乘法运算,属于有理数中哪些数 的运算?
问题三: 计算下列各题;
(1)9×12 =
(2)2.5×8=
(3)0×2.75=
(4)0×0=
以上这些题,都是对正有理数与正有理数、正有理数与零、 零与零的乘法,方法与小学学过的相同,今天我们要研究 的有理数的乘法运算,重点就是要解决引入负有理数之后, 怎样进行乘法运算的问题
知识回顾
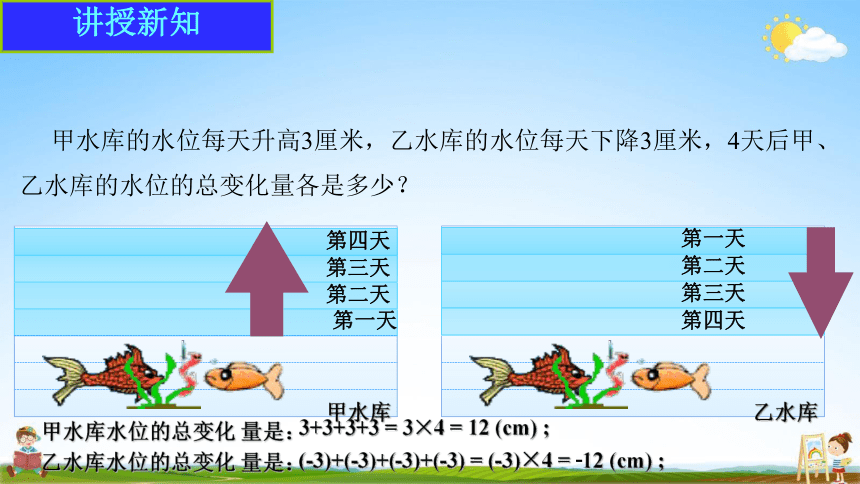
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、 乙水库的水位的总变化量各是多少?
第一天
第四天 第三天 第二天
第一天 第二天 第三天 第四天
-
讲授新知
水库水位的变化
,
,
,
,
2021-11-19
,
,
,
,
归纳
(3)若ab>0,则a、b应满足什么条件? (4)若ab<0,则a、b应满足什么条件?
a、b同号 a、b异号
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0. 讨论:
(1)若a<0,b>0,则ab < 0 ;
(2)若a<0,b<0,则ab > 0 ;
例1 计算: (1)9×6 ;
(2)( 9)×6 ;
解:
(1) 9×6
= +(9×6)
= 54 ;
(3) 3×(-4)
(2) ( 9)×6
= (9×6)
= 54;
(4)(-3)×(-4)
= 12;
有理数乘法的求解 步骤:
先确定积的符号
再确定
积的绝对值
= (3 ×4)
= +(3×4)
= 12;
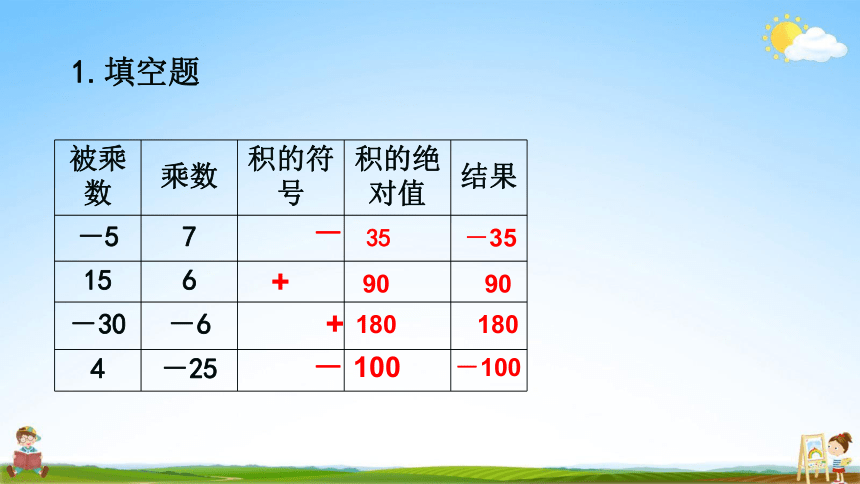
1.填空题
被乘 数 乘数 积的符 号 积的绝 对值 结果
-5 7 - 35 -35
15 6 + 90 90
-30 -6 + 180 180
4 -25 - 100 -100
2、确定乘积符号,并计算结果:
(1)7×(-9);
(2)4×5;
(3)(-7)×(-9)
(4)(-12)×3.
(6)-2009×0
3
( 4 ) 0 . 3
2
( 1 ) 1
10
4 ) ( 7 )
7 4
( 3 )(
2
( 2 )( 1 ) ( 2 )
2
1
a
例2、 用正负数表示气温的变化量,上升为正,下降为负。 登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀 登3km后,气温有什么变化?
解:(-6)×3=-18 答:气温下降18℃。
商店降价销售某种商品,每件降5元,售出60件后,与 按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.
( 1 ) . 2 3 4 5
( 2 ) . 2 3 4 5
( 3 ) . 2 3 4 5
( 4 ) . 2 3 4 5 ( 5 ) . 2 3 4 0 5 ( 6 )( 2 ) 3 4 5 0
归纳:
当负因数的个数为奇数时,积为_负 ; 当负因数的个数为偶数时,积为_正 。
结论1:几个不等于0的数相乘,积的符号由 负因数的个数 决定;
结论2:有一个因数为0,则积为_0 ;
(1 ) . 2 3 4 1
( 2 ) . 2 3 5 6
( 3 ) . 2 2 2
( 4 ) . 3 3 3 3
( 5 ). 5 ( 4 ) 0 ( 9 )
( 6 ). 5 4 10 ( 9 )
5
4
( 1 ) ( 3 )
( 9 ) ( 1 ) ;
1
4
6
( 2 ) ( 5 ) 6
5
( 4 )
5
例3 计算:
解:(1)原式
5
9 1 )
6 5 4
2 7
8
( 3
4 1
5 4
(2)原式 5 6
6
先确定积的符号
再确定积的绝对值
12 15 2 3
5 8 1 2
(1) (-5)×8×(-7)×(-0.25)
=-5×8×7×0.25
=-70
27
2
12 15 2 3
5 8 1 2
(2)
15 2
8
3
3 2 0 1
4
1 5
(3)
=0
当堂练习
1、已知a、b互为相反数,c、d互为倒数,e是绝
对值最小的数,计算:(a+b)+ - (a+b)e
1
cd
2、已知|x|=2,|y|=3,且xy<0,则x-y= 5或-5 .
3.已知5个数的积为负数,则其中负因数的个数是1_或3或5
4.填空(用“>”或“<”号连接):
(1)如果 a<0,b<0,那么 ab 0;
A. a>0,b>0 C. a>0,b<0
B. a<0,b<0
D. a>0,b>0或a<0,b<0
6.若ab=0,则一定有( B )
A. a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
<
(2)如果 a<0,b﹥0,那么ab > 0;
5. 若 ab>0,则必有 ( D )
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何 数同0相乘,都得0.
几个不是零的数相乘,负因数的个数为 奇数时积为负数
偶数时积为正数
课堂总结
几个数相乘若有因数为零则积为零.
有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
乘积是1的两个数互为倒数.
谢谢观看
Thank You
第一章 有理数
1.4.1 有理数的乘法法则
人教版 数学 七年级 上册
知识与技能:
经历探索有理数乘法法则过程,掌握有理数的乘法法则,能用法则进 行有理数的乘法.
过程与方法:
经历探索有理数乘法法则的过程,发展学生归纳、猜想、验证等能 力.
情感态度与价值观:
培养学生积极探索精神,感受数学与实际生活的联系. 重点:应用法则正确地进行有理数乘法运算.
难点:两负数相乘,积的符号为正与两负数相加和的符号为负号容易 混淆.
学习目标
问题一:有理数包括哪些数?
问题二:小学已经学过的乘法运算,属于有理数中哪些数 的运算?
问题三: 计算下列各题;
(1)9×12 =
(2)2.5×8=
(3)0×2.75=
(4)0×0=
以上这些题,都是对正有理数与正有理数、正有理数与零、 零与零的乘法,方法与小学学过的相同,今天我们要研究 的有理数的乘法运算,重点就是要解决引入负有理数之后, 怎样进行乘法运算的问题
知识回顾
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、 乙水库的水位的总变化量各是多少?
第一天
第四天 第三天 第二天
第一天 第二天 第三天 第四天
-
讲授新知
水库水位的变化
,
,
,
,
2021-11-19
,
,
,
,
归纳
(3)若ab>0,则a、b应满足什么条件? (4)若ab<0,则a、b应满足什么条件?
a、b同号 a、b异号
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0. 讨论:
(1)若a<0,b>0,则ab < 0 ;
(2)若a<0,b<0,则ab > 0 ;
例1 计算: (1)9×6 ;
(2)( 9)×6 ;
解:
(1) 9×6
= +(9×6)
= 54 ;
(3) 3×(-4)
(2) ( 9)×6
= (9×6)
= 54;
(4)(-3)×(-4)
= 12;
有理数乘法的求解 步骤:
先确定积的符号
再确定
积的绝对值
= (3 ×4)
= +(3×4)
= 12;
1.填空题
被乘 数 乘数 积的符 号 积的绝 对值 结果
-5 7 - 35 -35
15 6 + 90 90
-30 -6 + 180 180
4 -25 - 100 -100
2、确定乘积符号,并计算结果:
(1)7×(-9);
(2)4×5;
(3)(-7)×(-9)
(4)(-12)×3.
(6)-2009×0
3
( 4 ) 0 . 3
2
( 1 ) 1
10
4 ) ( 7 )
7 4
( 3 )(
2
( 2 )( 1 ) ( 2 )
2
1
a
例2、 用正负数表示气温的变化量,上升为正,下降为负。 登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀 登3km后,气温有什么变化?
解:(-6)×3=-18 答:气温下降18℃。
商店降价销售某种商品,每件降5元,售出60件后,与 按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.
( 1 ) . 2 3 4 5
( 2 ) . 2 3 4 5
( 3 ) . 2 3 4 5
( 4 ) . 2 3 4 5 ( 5 ) . 2 3 4 0 5 ( 6 )( 2 ) 3 4 5 0
归纳:
当负因数的个数为奇数时,积为_负 ; 当负因数的个数为偶数时,积为_正 。
结论1:几个不等于0的数相乘,积的符号由 负因数的个数 决定;
结论2:有一个因数为0,则积为_0 ;
(1 ) . 2 3 4 1
( 2 ) . 2 3 5 6
( 3 ) . 2 2 2
( 4 ) . 3 3 3 3
( 5 ). 5 ( 4 ) 0 ( 9 )
( 6 ). 5 4 10 ( 9 )
5
4
( 1 ) ( 3 )
( 9 ) ( 1 ) ;
1
4
6
( 2 ) ( 5 ) 6
5
( 4 )
5
例3 计算:
解:(1)原式
5
9 1 )
6 5 4
2 7
8
( 3
4 1
5 4
(2)原式 5 6
6
先确定积的符号
再确定积的绝对值
12 15 2 3
5 8 1 2
(1) (-5)×8×(-7)×(-0.25)
=-5×8×7×0.25
=-70
27
2
12 15 2 3
5 8 1 2
(2)
15 2
8
3
3 2 0 1
4
1 5
(3)
=0
当堂练习
1、已知a、b互为相反数,c、d互为倒数,e是绝
对值最小的数,计算:(a+b)+ - (a+b)e
1
cd
2、已知|x|=2,|y|=3,且xy<0,则x-y= 5或-5 .
3.已知5个数的积为负数,则其中负因数的个数是1_或3或5
4.填空(用“>”或“<”号连接):
(1)如果 a<0,b<0,那么 ab 0;
A. a>0,b>0 C. a>0,b<0
B. a<0,b<0
D. a>0,b>0或a<0,b<0
6.若ab=0,则一定有( B )
A. a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
<
(2)如果 a<0,b﹥0,那么ab > 0;
5. 若 ab>0,则必有 ( D )
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何 数同0相乘,都得0.
几个不是零的数相乘,负因数的个数为 奇数时积为负数
偶数时积为正数
课堂总结
几个数相乘若有因数为零则积为零.
有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
乘积是1的两个数互为倒数.
谢谢观看
Thank You
