2021-2022学年高一上学期数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图像 课件(共33张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图像 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 15:16:17 | ||
图片预览





文档简介
(共33张PPT)
(1) 正比例函数: y=2x
(2) 一次函数: y=-x+2
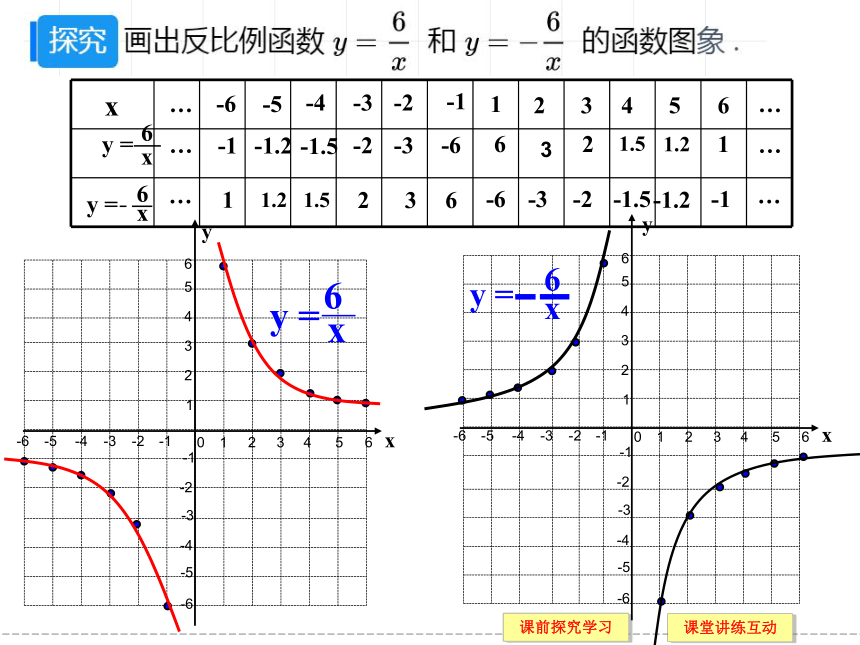
(3) 反比例函数:
(4) 二次函数: y=x2
画出如下函数的图像:
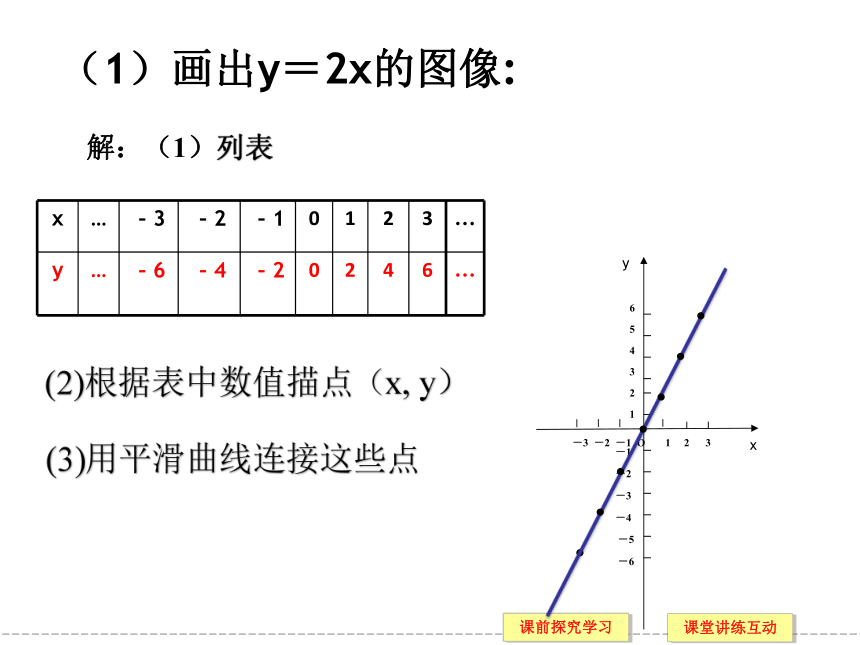
(1)画出y=2x的图像:
解:(1)列表
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
(2)根据表中数值描点(x, y)
(3)用平滑曲线连接这些点
-1
-2
-3
-4
-5
-6
1 2 3
-3 -2 -1 O
6
5
4
3
2
1
x
y
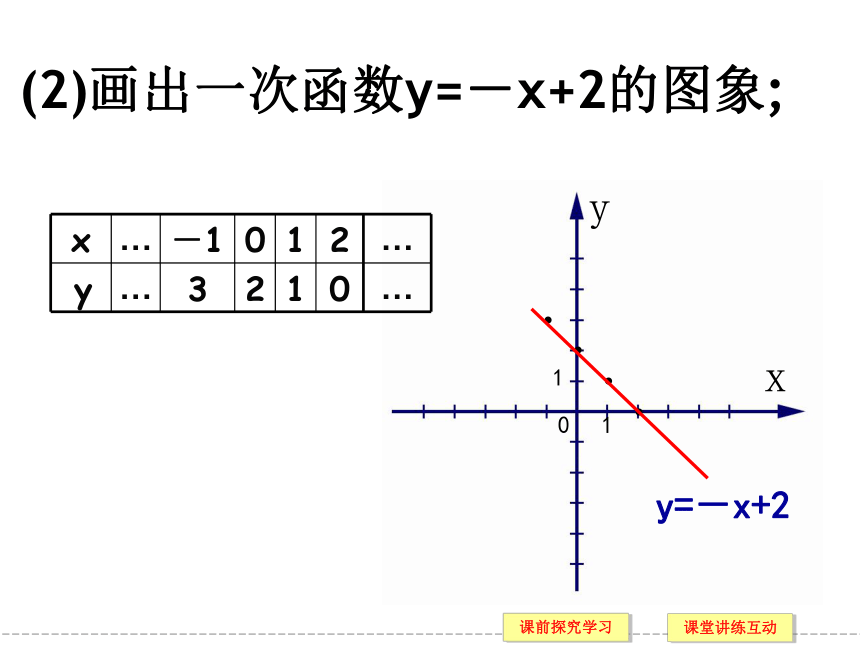
(2)画出一次函数y=-x+2的图象;
x … -1 0 1 2 …
y … 3 2 1 0 …
y=-x+2
x
y
0
1
1
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
6
-5
-1
-2
-3
-4
-6
…
…
…
-1
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
…
…
y =
x
6
…
-1.5
6
2
1.5
1.2
1
-6
-3
-2
-1.2
-1
3
y =
x
6
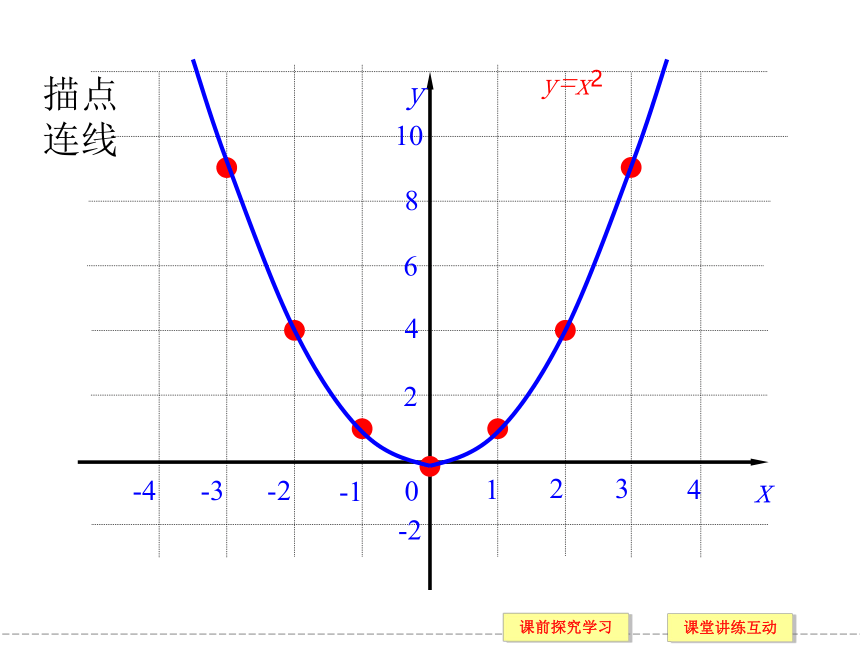
(4) 用描点法画二次函数y=x2的图象
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
1
0
4
9
观察y=x2的表达式,选择适当x值,并计算
相应的y值,完成下表:
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点
连线
y=x2
三角函数:
对应关系y=sinx表示的函数为正弦函数;
对应关系y=cosx表示的函数为余弦函数;
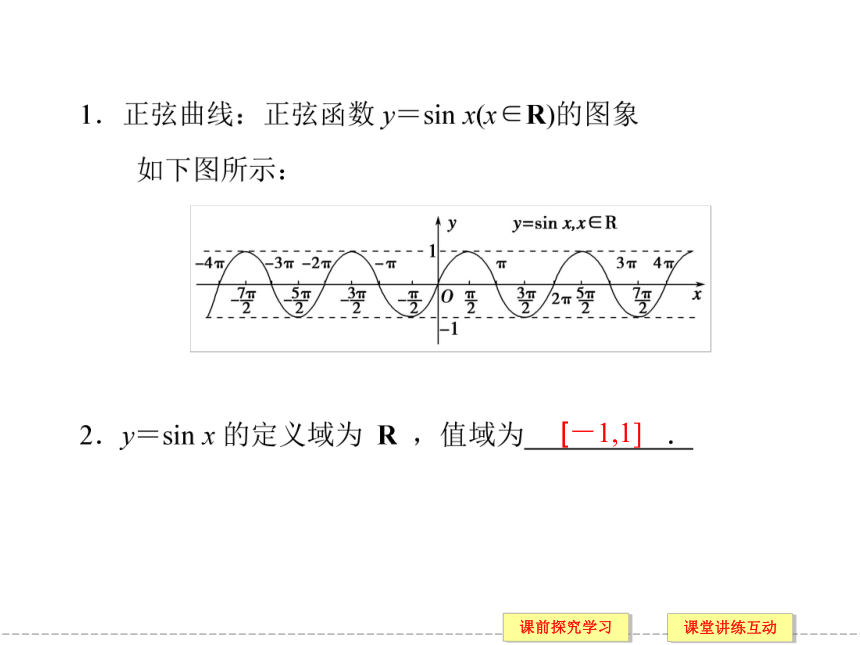
两个函数的定义域都是
P(x,y)
O
x
y
M
α
正弦线是MP
余弦线是OM
R
描点法是做函数图像的基本方法
如何画出函数y=sinx(x的单位是弧度)
的图像呢?
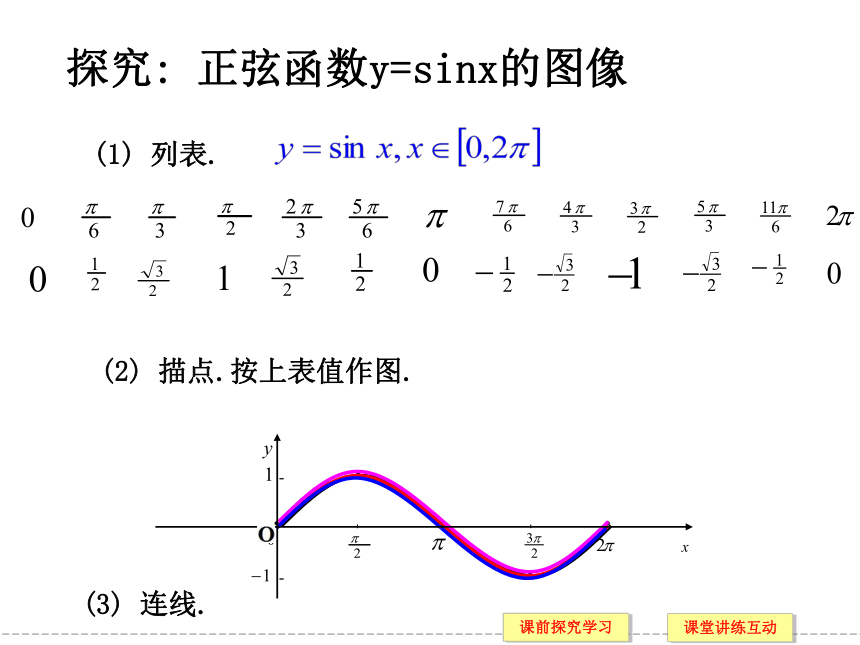
(1) 列表.
(2) 描点.按上表值作图.
(3) 连线.
-
-
-
-
-
-
探究: 正弦函数y=sinx的图像
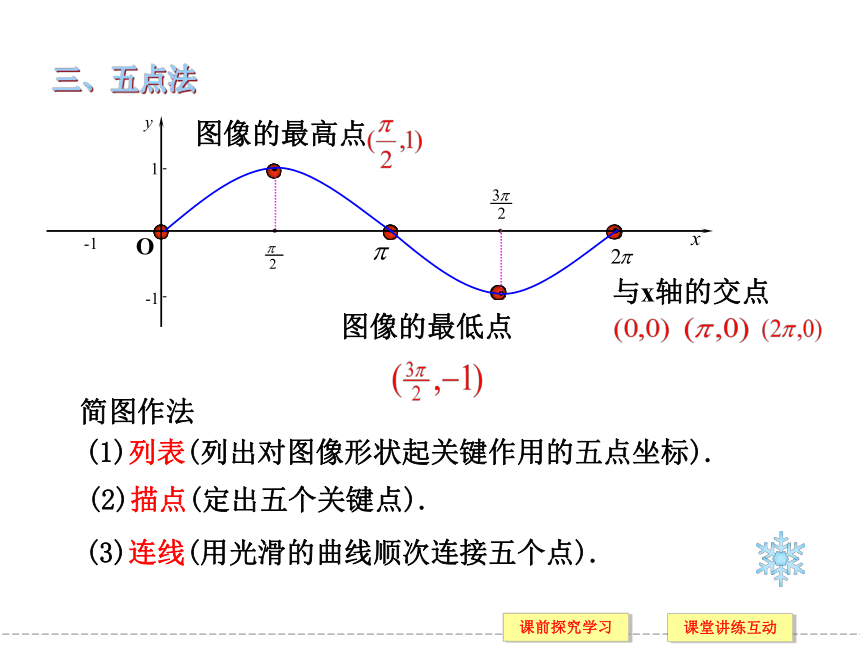
与x轴的交点
图像的最高点
图像的最低点
三、五点法
-
-
-1
1
-1
简图作法
(1)列表(列出对图像形状起关键作用的五点坐标).
(3)连线(用光滑的曲线顺次连接五个点).
(2)描点(定出五个关键点).
O
[-1,1]
函数
图像的几何作法
作法:
(1)等分.
(2)作正弦线.
(3)平移.
(4)连线.
方法二、正弦线做图像
分组讨论
如何作出余弦函数的图象?
知识探究(二):余弦函数的图象
1
-1
x
y
o
余弦函数的“五点作图法”
五点法的规律是:
横轴五点排均匀,上下顶点圆滑行;
上凸下凹形相似, 游走酷似波浪行.
x
cosx
0
1
-1
0
1
余弦函数的图象
思考:如何将余弦函数用诱导公式写成正弦函数?
余弦函数的图象可以将正弦曲线向左平移 个单位长度而得到,余弦函数的图象叫做余弦曲线.
知识探究(二):余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
余弦函数的图象
正弦函数的图象
y=cosx=sin(x+ ), x R
例1.作出
函数y=1+sinx,x∈[0,2π]的简图.
解:列表
描点并将它们用光滑的曲线连接起来:
题型一:利用五点法做出相应函数的图像:
x
y
O
-1
1
2
2
.
.
.
.
.
[0,2π]
x
sinx,
y
=
思考: 函数 y=1+sinx, x∈[0, 2π]与
函数 y=sinx,x∈[0, 2π]的图象之间有何联系?
1
-1
y= -sinx, x [0, ]
解:列表
x
y
例2.用五点法画出y=-sinx在区间[0,2π]上的简图.
x 0
y=sinx 0 1 0 -1 0
y=-sinx 0 -1 0 1 0
.
.
.
.
O
x 0
例3 利用五点法画出函数y=sinx-1的简图
y=sinx
y=sinx-1
解:列表
0 1 0 -1 0
-1 0 -1 -2 -1
画出简图
针对性练习.
画出函数y=-cosx, x∈[0, 2π]的简图.
解:(1)列表
(2)描点,连线
思考:函数y=- cosx与函数y=cosx, x∈[0,2π]的图象有何联系?
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
D
的大致图象为( )
x∈[0,2π]
函数y=1-cos x,
变式训练:
x
y
O
2π
π
1
-1
题型2:
例1 当x∈[0,2π]时,
求不等式 的解集.
x
-1
O
2π
π
1
y
π
3π
例2. 当x∈[0,2π]时,
求不等式 的解集.
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线:
正弦曲线:
正余弦函数的性质之一:对称性和奇偶性
【探究】观察正弦曲线和余弦曲线,可以看到正弦曲线关于原点O对称,余弦曲
线关于y轴对称. 也可由诱导公式=;=得到
所以正弦函数是奇函数,余弦函数是偶函数.
对称性:
正弦曲线和余弦曲线即是中心对称图形,又是轴对称图形.
Ⅰ.函数的对称轴是直线,对称中心是.
Ⅱ.函数的对称轴是直线,对称中心是.
1. 正弦曲线、余弦曲线作法
几何作图法(三角函数线)
描点法(五点法)
图象变换法
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
2.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线,掌握正弦曲线和余弦曲线之间的区别与联系.
课堂小结:
(二)正弦函数、余弦函数
函数 y=sin x y=cos x
图象
定义域 R R
值域 【-1,1】 【-1,1】
图像画法 五点法、正弦线法 五点法、图像平移法
关键五点
奇偶性 ______ _______
奇函数
偶函数
课 后 作 业
1.课本P200页练习题1-4
2.金版新学案5.4.1正余弦函数的图像和课时作业四十六完成
3.预习正弦函数、余弦函数的性质.
(1) 正比例函数: y=2x
(2) 一次函数: y=-x+2
(3) 反比例函数:
(4) 二次函数: y=x2
画出如下函数的图像:
(1)画出y=2x的图像:
解:(1)列表
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
(2)根据表中数值描点(x, y)
(3)用平滑曲线连接这些点
-1
-2
-3
-4
-5
-6
1 2 3
-3 -2 -1 O
6
5
4
3
2
1
x
y
(2)画出一次函数y=-x+2的图象;
x … -1 0 1 2 …
y … 3 2 1 0 …
y=-x+2
x
y
0
1
1
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
6
-5
-1
-2
-3
-4
-6
…
…
…
-1
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
…
…
y =
x
6
…
-1.5
6
2
1.5
1.2
1
-6
-3
-2
-1.2
-1
3
y =
x
6
(4) 用描点法画二次函数y=x2的图象
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
1
0
4
9
观察y=x2的表达式,选择适当x值,并计算
相应的y值,完成下表:
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点
连线
y=x2
三角函数:
对应关系y=sinx表示的函数为正弦函数;
对应关系y=cosx表示的函数为余弦函数;
两个函数的定义域都是
P(x,y)
O
x
y
M
α
正弦线是MP
余弦线是OM
R
描点法是做函数图像的基本方法
如何画出函数y=sinx(x的单位是弧度)
的图像呢?
(1) 列表.
(2) 描点.按上表值作图.
(3) 连线.
-
-
-
-
-
-
探究: 正弦函数y=sinx的图像
与x轴的交点
图像的最高点
图像的最低点
三、五点法
-
-
-1
1
-1
简图作法
(1)列表(列出对图像形状起关键作用的五点坐标).
(3)连线(用光滑的曲线顺次连接五个点).
(2)描点(定出五个关键点).
O
[-1,1]
函数
图像的几何作法
作法:
(1)等分.
(2)作正弦线.
(3)平移.
(4)连线.
方法二、正弦线做图像
分组讨论
如何作出余弦函数的图象?
知识探究(二):余弦函数的图象
1
-1
x
y
o
余弦函数的“五点作图法”
五点法的规律是:
横轴五点排均匀,上下顶点圆滑行;
上凸下凹形相似, 游走酷似波浪行.
x
cosx
0
1
-1
0
1
余弦函数的图象
思考:如何将余弦函数用诱导公式写成正弦函数?
余弦函数的图象可以将正弦曲线向左平移 个单位长度而得到,余弦函数的图象叫做余弦曲线.
知识探究(二):余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
余弦函数的图象
正弦函数的图象
y=cosx=sin(x+ ), x R
例1.作出
函数y=1+sinx,x∈[0,2π]的简图.
解:列表
描点并将它们用光滑的曲线连接起来:
题型一:利用五点法做出相应函数的图像:
x
y
O
-1
1
2
2
.
.
.
.
.
[0,2π]
x
sinx,
y
=
思考: 函数 y=1+sinx, x∈[0, 2π]与
函数 y=sinx,x∈[0, 2π]的图象之间有何联系?
1
-1
y= -sinx, x [0, ]
解:列表
x
y
例2.用五点法画出y=-sinx在区间[0,2π]上的简图.
x 0
y=sinx 0 1 0 -1 0
y=-sinx 0 -1 0 1 0
.
.
.
.
O
x 0
例3 利用五点法画出函数y=sinx-1的简图
y=sinx
y=sinx-1
解:列表
0 1 0 -1 0
-1 0 -1 -2 -1
画出简图
针对性练习.
画出函数y=-cosx, x∈[0, 2π]的简图.
解:(1)列表
(2)描点,连线
思考:函数y=- cosx与函数y=cosx, x∈[0,2π]的图象有何联系?
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
D
的大致图象为( )
x∈[0,2π]
函数y=1-cos x,
变式训练:
x
y
O
2π
π
1
-1
题型2:
例1 当x∈[0,2π]时,
求不等式 的解集.
x
-1
O
2π
π
1
y
π
3π
例2. 当x∈[0,2π]时,
求不等式 的解集.
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线:
正弦曲线:
正余弦函数的性质之一:对称性和奇偶性
【探究】观察正弦曲线和余弦曲线,可以看到正弦曲线关于原点O对称,余弦曲
线关于y轴对称. 也可由诱导公式=;=得到
所以正弦函数是奇函数,余弦函数是偶函数.
对称性:
正弦曲线和余弦曲线即是中心对称图形,又是轴对称图形.
Ⅰ.函数的对称轴是直线,对称中心是.
Ⅱ.函数的对称轴是直线,对称中心是.
1. 正弦曲线、余弦曲线作法
几何作图法(三角函数线)
描点法(五点法)
图象变换法
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
2.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线,掌握正弦曲线和余弦曲线之间的区别与联系.
课堂小结:
(二)正弦函数、余弦函数
函数 y=sin x y=cos x
图象
定义域 R R
值域 【-1,1】 【-1,1】
图像画法 五点法、正弦线法 五点法、图像平移法
关键五点
奇偶性 ______ _______
奇函数
偶函数
课 后 作 业
1.课本P200页练习题1-4
2.金版新学案5.4.1正余弦函数的图像和课时作业四十六完成
3.预习正弦函数、余弦函数的性质.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
