2021-2022学年华东师大版八年级上学期数学期末练习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版八年级上学期数学期末练习试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 11:28:38 | ||
图片预览




文档简介
2021-2022学年华东师大新版八年级上学期数学期末练习试卷一.选择题(共10小题,满分30分,每小题3分)
1.下列计算正确的是 ( )
A. B. C.﹣22=4 D.(﹣2)3=﹣6
2.下列运算错误的是( )
A.(2b3)2=4b9 B.a2 a3=a5
C.(a2)3=a6 D.a3÷a2=a(a≠0)
3.下列说法不正确的是( )
A.两边和它们的夹角分别相等的两个三角形全等
B.两角分别相等且其中一组等角的对边相等的两个三角形全等
C.底边和顶角分别相等的两个等腰三角形全等
D.两边和其中一边的对角分别相等的两个三角形全等
4.某学校七年级(4)班40位同学都订阅了一本杂志,10%的同学订阅《科学画报》,40%的同学订阅《作文通讯》,30%的同学订阅《英语画刊》,20%的同学订阅其他杂志能表示上述数据的统计图是( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.以上答案均不对
5.已知三角形的三边长为6,8,10,则这个三角形最长边上的高是( )
A.10 B.8 C.2.4 D.4.8
6.用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
7.要说明命题“若a>b,则a2>b2”是假命题,可设( )
A.a=3,b=4 B.a=4,b=3 C.a=﹣3,b=﹣4 D.a=﹣4,b=﹣3
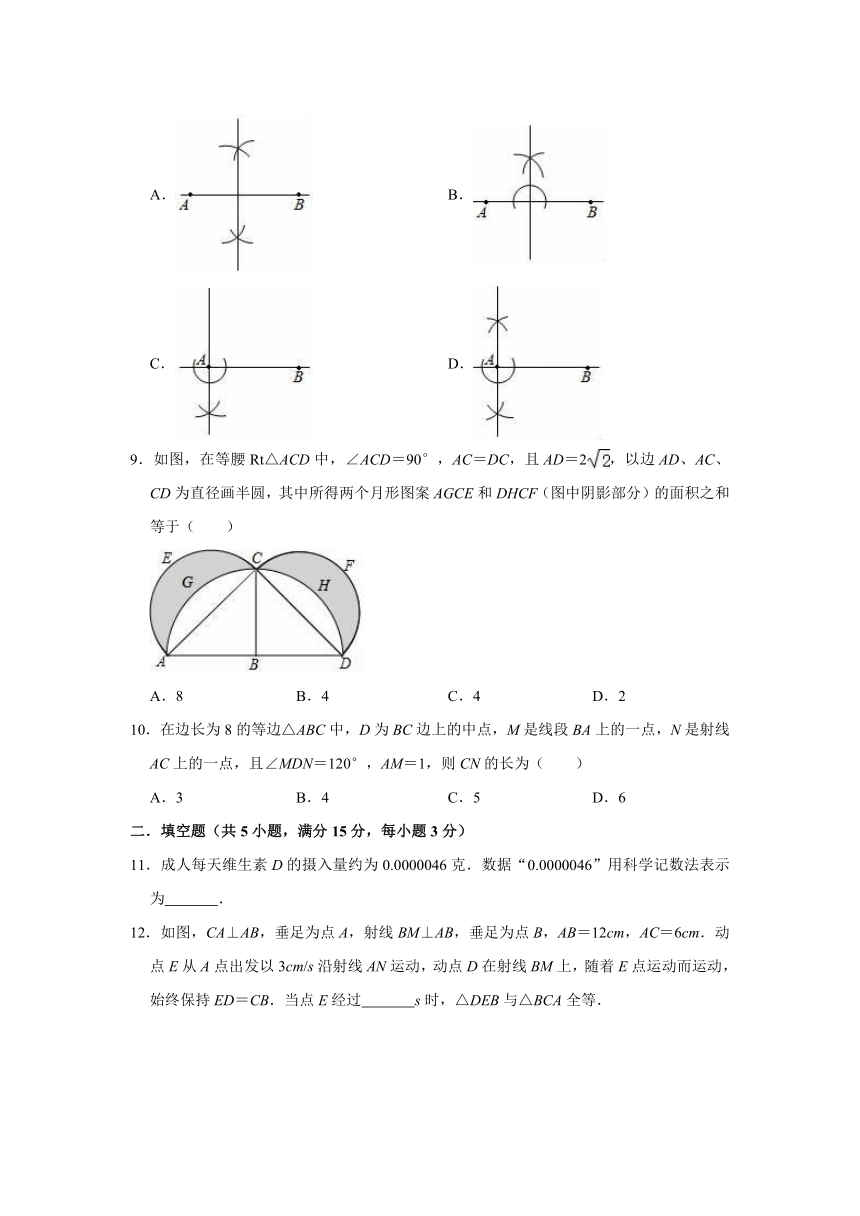
8.过点A作直线AB的垂线,符合要求的作图痕迹是( )
A. B.
C. D.
9.如图,在等腰Rt△ACD中,∠ACD=90°,AC=DC,且AD=2,以边AD、AC、CD为直径画半圆,其中所得两个月形图案AGCE和DHCF(图中阴影部分)的面积之和等于( )
A.8 B.4 C.4 D.2
10.在边长为8的等边△ABC中,D为BC边上的中点,M是线段BA上的一点,N是射线AC上的一点,且∠MDN=120°,AM=1,则CN的长为( )
A.3 B.4 C.5 D.6
二.填空题(共5小题,满分15分,每小题3分)
11.成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为 .
12.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=12cm,AC=6cm.动点E从A点出发以3cm/s沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.当点E经过 s时,△DEB与△BCA全等.
13.若am=6,an=4,则a2m﹣n= .
14.如图,已知点P是射线BM上一动点(P不与B重合),∠AOB=30°,∠ABM=60°,当∠OAP= 时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形.
15.如图,在△ABC中,∠C=90°,AD平分∠CAB;DE⊥AB于E,若AC=8,则AE= .
三.解答题(共8小题,满分75分)
16.(12分)计算与化简
(1).
(2)(2x+y)(2x﹣y)﹣(x﹣2y)2+y(﹣4x+5y+1).
17.(8分)如图在四边形ABCD中AB=BC=,CD=,AD=1且AB⊥CB,试求四边形ABCD的面积(提示:连接AC).
18.(8分)分解因式:
(1)﹣3a2+6ab﹣3b2;
(2)9a2(x﹣y)+4b2(y﹣x).
19.(8分)在“世界读书日”前夕,某校开展了“阅读助我成长”的读书活动.读书活动结束后,学校统计了全校学生课外阅读书籍的数量,将收集的数据整理成如下不完整的统计表和扇形图.
学生读书数量统计表
阅读量/本 学生人数
1 480
2 a
3 b
4 160
(1)求a,b的值.
(2)该校全体学生在这次活动中课外阅读书籍的总量是多少本?
20.(8分)已知:如图,△ABC.
(1)请用直尺和圆规,按以下要求作图(保留作图痕迹).
作法:①作AD平分∠BAC交BC于点D;
②作线段AD的垂直平分线分别交AB于点E,交AC于点F;
③连接DE,DF;
(2)在(1)所作的图中,试判断四边形AEDF的形状,并说明理由.
21.(9分)尺规作图:作无理数.
作法:
①在数轴上点A,B,C分别表示﹣2,﹣1,0,分别以点A,B为圆心,AB长为半径画弧,两弧交于点D;
②连接CD,以点C为圆心,CD长为半径画弧,交数轴正半轴于点P.则点P表示的数就是无理数.
(1)判断△ACD的形状,并说明理由;
(2)说明点P表示的数就是无理数的理由.
22.(9分)已知a,b,c为△ABC的三条边的长,当b2+2ab=c2+2ac时,
(1)试判断△ABC属于哪一类三角形;
(2)若a=4,b=3,求△ABC的周长.
23.(13分)如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.
(1)在图中,依题意补全图形;
(2)记∠DAC=α (α<45° ),求∠ABF 的大小;(用含α 的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、=4,所以A选项错误;
B、﹣=﹣3,所以B选项正确;
C、﹣22=﹣4,所以C选项错误;
D、(﹣2)3=﹣8,所以D选项错误.
故选:B.
2.解:A.(2b3)2=4b6,故本选项符合题意;
B.a2 a3=a5,故本选项不合题意;
C.(a2)3=a6,故本选项不合题意;
D.a3÷a2=a(a≠0),故本选项不合题意.
故选:A.
3.解:A、两边和它们的夹角分别相等的两个三角形全等,所以A选项的说法正确;
B、两角分别相等且其中一组等角的对边相等的两个三角形全等,所以B选项的说法正确;
C、底边和顶角分别相等的两个等腰三角形全等,所以C选项的说法正确;
D、两边和其中一边的对角分别相等的两个三角形不一定全等,所以D选项的说法不正确.
故选:D.
4.解:反映七(4)班同学订阅各种杂志所占的百分比,符合扇形统计图的特点,
故选:C.
5.解:∵62+82=102,
∴这个三角形是直角三角形,
∴边长为10的边上的高为6×8÷10=4.8.
故选:D.
6.解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
7.解:当a=﹣3,b=﹣4时,a2=9,b2=16,
a>b,而a2<b2,
∴命题“若a>b,则a2>b2”是假命题,
故选:C.
8.解:由过直线上一点作已知直线的垂线的方法可知,选项C符合题意.
故选:C.
9.解:在等腰Rt△ACD中,∠ACD=90°,AC=DC,AD=2,
∴AC2+DC2=AD2=8,
∴AC=CD=2,
∴S△ACD=AC DC=2,
∴S阴影=π()2+S△ACD﹣π()2
=π+2﹣π
=2,
故选:D.
10.解:如图,在AC的延长线上取点E,使得CE=CD,
则∠CDE=∠CED=30°,
∴∠ADE=120°,∠MDN=120°,
∴∠MDA=∠NDE,
∵∠MAD=∠NED=30°,
∵AD=DE,
在△MDA与△NDE中,
,
∴△MDA≌△NDE(AAS),
∴NE=MA=1,
∴CN=4﹣1=3,
故选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:0.0000046=4.6×10﹣6.
故答案为:4.6×10﹣6.
12.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6,
∴BE=6,
∴AE=12﹣6=6,
∴点E的运动时间为6÷3=2(秒);
②当E在BN上,AC=BE时,
AC=12+6=18,
点E的运动时间为18÷3=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=12+12=24,
点E的运动时间为24÷3=8(秒),
故答案为:0,2,6,8.
13.解:∵am=6,an=4,
∴a2m﹣n=(am)2÷an=62÷4=36÷4=9.
故答案为:9.
14.解:分为以下5种情况:
①OA=OP,
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=(180°﹣30°)=75°;
②OA=AP,
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣30°=120°;
③AB=AP,
∵∠AOM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
④AB=BP,
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=(180°﹣60°)=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
⑤AP=BP,
∵∠ABM=60°,AP=BP,
∴∠ABM=∠PAB=60°,
∴∠APO=180°﹣60°﹣60°=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.
15.解:∵∠C=90°,AD平分∠CAB;DE⊥AB于E,
∴CD=DE,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=8.
故答案为:8.
三.解答题(共8小题,满分75分)
16.解:(1)
=2﹣3﹣(﹣1)
=2﹣3﹣+1
=﹣;
(2)(2x+y)(2x﹣y)﹣(x﹣2y)2+y(﹣4x+5y+1)
=(2x)2﹣y2﹣(x2﹣4xy+4y2)+(﹣4xy+5y2+y)
=4x2﹣y2﹣x2+4xy﹣4y2﹣4xy+5y2+y
=3x2+y.
17.解:连结AC
∵AB⊥CB,
∴AC2=AB2+BC2,
∴AC===2,
又∵CD=,AD=1,
∴AD2+CD2=12+()2=4=22=AC2,
∴△ACD为直角三角形,
∴S△ABC===1,
S△ACD===,
∴S四边形ABCD=S△ABC+S△ACD=1+.
18.解:(1)原式=﹣3(a2﹣2ab+b2)=﹣3(a﹣b)2;
(2)原式=(x﹣y)(3a+2b)(3a﹣2b).
19.解:(1)调查的全部人数:480÷30%=1600(人),
阅读3本数量:b=1600×40%=640(人),
阅读2本数量:a=1600﹣480﹣640﹣160=320(人),
答:a的值为320人,b的值为640人.
(2)阅读总量:1×480+2×320+3×640+4×160=3680(本),
答:全校阅读总量为3680本.
20.解:(1)如图所示,即为所求作的图形.
(2)结论:四边形AEDF是菱形.
理由:∵EF垂直平分线段AD,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠EAD=∠DAC,
∴∠EDA=∠DAC,
∴DE∥AC,
同理可得,DF∥AE,
∴四边形AEDF是平行四边形,
∵AE=DF,
∴四边形AEDF是菱形.
21.解:(1)△ACD是直角三角形,
理由:由题意可得,
AD=AB=BD=BC=1,
∴△ABD是等边三角形,∠BDC=∠BCD,
∴∠DAB=60°,∠DBA=60°,
∵∠DBA=∠BDC+∠BCD,
∴∠BCD=30°,
∴∠ADC=180°﹣∠DAB﹣∠BCD=90°,
∴△ACD是直角三角形;
(2)∵△ACD是直角三角形,AD=1,AC=2,∠ADC=90°,
∴CD===,
∵CD=CP,
∴CP=,
∵点C表示的数为0,
∴点P表示的数就是无理数.
22.解:(1)△ABC是等腰三角形,理由如下:
∵a,b,c为△ABC的三条边的长,b2+2ab=c2+2ac,
∴b2﹣c2+2ab﹣2ac=0,
因式分解得:(b﹣c)(b+c+2a)=0,
∴b﹣c=0,
∴b=c,
∴△ABC是等腰三角形;
(2)∵a=4,b=3,
∴b=c=3,
∴△ABC的周长=a+b+c=4+3+3=10.
23.解:(1)如图1所示;
(2)如图2,
连接AE,由题意可知,∠EAD=∠CAD=α,AC=AE,
∴∠BAE=90°﹣2α,
∵AB=AC,
∴AB=AE,
∴∠ABE=∠AEB,
∴;
(3),
证明:如备用图,连接AE,CF,
由(2)可知,∠AEB=∠ABF=45°+α,
∵AB=AC,
∴∠ABC=45°,
∴∠CBF=α,
∵点C关于直线AD的对称点为点E,
∴∠ACF=∠AEF=135°﹣α,
∴∠BCF=90°﹣α,
∵∠CBF+∠BCF=90°,
∴△BCF是直角三角形.
∵△ACE是等边三角形,
∴α=30°.
∴∠CBF=30°
∴.
1.下列计算正确的是 ( )
A. B. C.﹣22=4 D.(﹣2)3=﹣6
2.下列运算错误的是( )
A.(2b3)2=4b9 B.a2 a3=a5
C.(a2)3=a6 D.a3÷a2=a(a≠0)
3.下列说法不正确的是( )
A.两边和它们的夹角分别相等的两个三角形全等
B.两角分别相等且其中一组等角的对边相等的两个三角形全等
C.底边和顶角分别相等的两个等腰三角形全等
D.两边和其中一边的对角分别相等的两个三角形全等
4.某学校七年级(4)班40位同学都订阅了一本杂志,10%的同学订阅《科学画报》,40%的同学订阅《作文通讯》,30%的同学订阅《英语画刊》,20%的同学订阅其他杂志能表示上述数据的统计图是( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.以上答案均不对
5.已知三角形的三边长为6,8,10,则这个三角形最长边上的高是( )
A.10 B.8 C.2.4 D.4.8
6.用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角 B.没有一个内角是直角
C.至少有一个内角是直角 D.每一个内角都不是直角
7.要说明命题“若a>b,则a2>b2”是假命题,可设( )
A.a=3,b=4 B.a=4,b=3 C.a=﹣3,b=﹣4 D.a=﹣4,b=﹣3
8.过点A作直线AB的垂线,符合要求的作图痕迹是( )
A. B.
C. D.
9.如图,在等腰Rt△ACD中,∠ACD=90°,AC=DC,且AD=2,以边AD、AC、CD为直径画半圆,其中所得两个月形图案AGCE和DHCF(图中阴影部分)的面积之和等于( )
A.8 B.4 C.4 D.2
10.在边长为8的等边△ABC中,D为BC边上的中点,M是线段BA上的一点,N是射线AC上的一点,且∠MDN=120°,AM=1,则CN的长为( )
A.3 B.4 C.5 D.6
二.填空题(共5小题,满分15分,每小题3分)
11.成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为 .
12.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=12cm,AC=6cm.动点E从A点出发以3cm/s沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.当点E经过 s时,△DEB与△BCA全等.
13.若am=6,an=4,则a2m﹣n= .
14.如图,已知点P是射线BM上一动点(P不与B重合),∠AOB=30°,∠ABM=60°,当∠OAP= 时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形.
15.如图,在△ABC中,∠C=90°,AD平分∠CAB;DE⊥AB于E,若AC=8,则AE= .
三.解答题(共8小题,满分75分)
16.(12分)计算与化简
(1).
(2)(2x+y)(2x﹣y)﹣(x﹣2y)2+y(﹣4x+5y+1).
17.(8分)如图在四边形ABCD中AB=BC=,CD=,AD=1且AB⊥CB,试求四边形ABCD的面积(提示:连接AC).
18.(8分)分解因式:
(1)﹣3a2+6ab﹣3b2;
(2)9a2(x﹣y)+4b2(y﹣x).
19.(8分)在“世界读书日”前夕,某校开展了“阅读助我成长”的读书活动.读书活动结束后,学校统计了全校学生课外阅读书籍的数量,将收集的数据整理成如下不完整的统计表和扇形图.
学生读书数量统计表
阅读量/本 学生人数
1 480
2 a
3 b
4 160
(1)求a,b的值.
(2)该校全体学生在这次活动中课外阅读书籍的总量是多少本?
20.(8分)已知:如图,△ABC.
(1)请用直尺和圆规,按以下要求作图(保留作图痕迹).
作法:①作AD平分∠BAC交BC于点D;
②作线段AD的垂直平分线分别交AB于点E,交AC于点F;
③连接DE,DF;
(2)在(1)所作的图中,试判断四边形AEDF的形状,并说明理由.
21.(9分)尺规作图:作无理数.
作法:
①在数轴上点A,B,C分别表示﹣2,﹣1,0,分别以点A,B为圆心,AB长为半径画弧,两弧交于点D;
②连接CD,以点C为圆心,CD长为半径画弧,交数轴正半轴于点P.则点P表示的数就是无理数.
(1)判断△ACD的形状,并说明理由;
(2)说明点P表示的数就是无理数的理由.
22.(9分)已知a,b,c为△ABC的三条边的长,当b2+2ab=c2+2ac时,
(1)试判断△ABC属于哪一类三角形;
(2)若a=4,b=3,求△ABC的周长.
23.(13分)如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.
(1)在图中,依题意补全图形;
(2)记∠DAC=α (α<45° ),求∠ABF 的大小;(用含α 的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、=4,所以A选项错误;
B、﹣=﹣3,所以B选项正确;
C、﹣22=﹣4,所以C选项错误;
D、(﹣2)3=﹣8,所以D选项错误.
故选:B.
2.解:A.(2b3)2=4b6,故本选项符合题意;
B.a2 a3=a5,故本选项不合题意;
C.(a2)3=a6,故本选项不合题意;
D.a3÷a2=a(a≠0),故本选项不合题意.
故选:A.
3.解:A、两边和它们的夹角分别相等的两个三角形全等,所以A选项的说法正确;
B、两角分别相等且其中一组等角的对边相等的两个三角形全等,所以B选项的说法正确;
C、底边和顶角分别相等的两个等腰三角形全等,所以C选项的说法正确;
D、两边和其中一边的对角分别相等的两个三角形不一定全等,所以D选项的说法不正确.
故选:D.
4.解:反映七(4)班同学订阅各种杂志所占的百分比,符合扇形统计图的特点,
故选:C.
5.解:∵62+82=102,
∴这个三角形是直角三角形,
∴边长为10的边上的高为6×8÷10=4.8.
故选:D.
6.解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
7.解:当a=﹣3,b=﹣4时,a2=9,b2=16,
a>b,而a2<b2,
∴命题“若a>b,则a2>b2”是假命题,
故选:C.
8.解:由过直线上一点作已知直线的垂线的方法可知,选项C符合题意.
故选:C.
9.解:在等腰Rt△ACD中,∠ACD=90°,AC=DC,AD=2,
∴AC2+DC2=AD2=8,
∴AC=CD=2,
∴S△ACD=AC DC=2,
∴S阴影=π()2+S△ACD﹣π()2
=π+2﹣π
=2,
故选:D.
10.解:如图,在AC的延长线上取点E,使得CE=CD,
则∠CDE=∠CED=30°,
∴∠ADE=120°,∠MDN=120°,
∴∠MDA=∠NDE,
∵∠MAD=∠NED=30°,
∵AD=DE,
在△MDA与△NDE中,
,
∴△MDA≌△NDE(AAS),
∴NE=MA=1,
∴CN=4﹣1=3,
故选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:0.0000046=4.6×10﹣6.
故答案为:4.6×10﹣6.
12.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6,
∴BE=6,
∴AE=12﹣6=6,
∴点E的运动时间为6÷3=2(秒);
②当E在BN上,AC=BE时,
AC=12+6=18,
点E的运动时间为18÷3=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=12+12=24,
点E的运动时间为24÷3=8(秒),
故答案为:0,2,6,8.
13.解:∵am=6,an=4,
∴a2m﹣n=(am)2÷an=62÷4=36÷4=9.
故答案为:9.
14.解:分为以下5种情况:
①OA=OP,
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=(180°﹣30°)=75°;
②OA=AP,
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣30°=120°;
③AB=AP,
∵∠AOM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
④AB=BP,
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=(180°﹣60°)=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
⑤AP=BP,
∵∠ABM=60°,AP=BP,
∴∠ABM=∠PAB=60°,
∴∠APO=180°﹣60°﹣60°=60°,
∴∠OAP=180°﹣∠AOB﹣∠APO=180°﹣30°﹣60°=90°;
所以当∠OAP=75°或120°或90°时,以A、O、B中的任意两点和P点为顶点的三角形是等腰三角形,
故答案为:75°或120°或90°.
15.解:∵∠C=90°,AD平分∠CAB;DE⊥AB于E,
∴CD=DE,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=8.
故答案为:8.
三.解答题(共8小题,满分75分)
16.解:(1)
=2﹣3﹣(﹣1)
=2﹣3﹣+1
=﹣;
(2)(2x+y)(2x﹣y)﹣(x﹣2y)2+y(﹣4x+5y+1)
=(2x)2﹣y2﹣(x2﹣4xy+4y2)+(﹣4xy+5y2+y)
=4x2﹣y2﹣x2+4xy﹣4y2﹣4xy+5y2+y
=3x2+y.
17.解:连结AC
∵AB⊥CB,
∴AC2=AB2+BC2,
∴AC===2,
又∵CD=,AD=1,
∴AD2+CD2=12+()2=4=22=AC2,
∴△ACD为直角三角形,
∴S△ABC===1,
S△ACD===,
∴S四边形ABCD=S△ABC+S△ACD=1+.
18.解:(1)原式=﹣3(a2﹣2ab+b2)=﹣3(a﹣b)2;
(2)原式=(x﹣y)(3a+2b)(3a﹣2b).
19.解:(1)调查的全部人数:480÷30%=1600(人),
阅读3本数量:b=1600×40%=640(人),
阅读2本数量:a=1600﹣480﹣640﹣160=320(人),
答:a的值为320人,b的值为640人.
(2)阅读总量:1×480+2×320+3×640+4×160=3680(本),
答:全校阅读总量为3680本.
20.解:(1)如图所示,即为所求作的图形.
(2)结论:四边形AEDF是菱形.
理由:∵EF垂直平分线段AD,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠EAD=∠DAC,
∴∠EDA=∠DAC,
∴DE∥AC,
同理可得,DF∥AE,
∴四边形AEDF是平行四边形,
∵AE=DF,
∴四边形AEDF是菱形.
21.解:(1)△ACD是直角三角形,
理由:由题意可得,
AD=AB=BD=BC=1,
∴△ABD是等边三角形,∠BDC=∠BCD,
∴∠DAB=60°,∠DBA=60°,
∵∠DBA=∠BDC+∠BCD,
∴∠BCD=30°,
∴∠ADC=180°﹣∠DAB﹣∠BCD=90°,
∴△ACD是直角三角形;
(2)∵△ACD是直角三角形,AD=1,AC=2,∠ADC=90°,
∴CD===,
∵CD=CP,
∴CP=,
∵点C表示的数为0,
∴点P表示的数就是无理数.
22.解:(1)△ABC是等腰三角形,理由如下:
∵a,b,c为△ABC的三条边的长,b2+2ab=c2+2ac,
∴b2﹣c2+2ab﹣2ac=0,
因式分解得:(b﹣c)(b+c+2a)=0,
∴b﹣c=0,
∴b=c,
∴△ABC是等腰三角形;
(2)∵a=4,b=3,
∴b=c=3,
∴△ABC的周长=a+b+c=4+3+3=10.
23.解:(1)如图1所示;
(2)如图2,
连接AE,由题意可知,∠EAD=∠CAD=α,AC=AE,
∴∠BAE=90°﹣2α,
∵AB=AC,
∴AB=AE,
∴∠ABE=∠AEB,
∴;
(3),
证明:如备用图,连接AE,CF,
由(2)可知,∠AEB=∠ABF=45°+α,
∵AB=AC,
∴∠ABC=45°,
∴∠CBF=α,
∵点C关于直线AD的对称点为点E,
∴∠ACF=∠AEF=135°﹣α,
∴∠BCF=90°﹣α,
∵∠CBF+∠BCF=90°,
∴△BCF是直角三角形.
∵△ACE是等边三角形,
∴α=30°.
∴∠CBF=30°
∴.
同课章节目录
