5.5.2简单的三角恒等变换-2021-2022学年高一数学上学期同步课件(人教A版2019必修第一册)(共47张PPT)
文档属性
| 名称 | 5.5.2简单的三角恒等变换-2021-2022学年高一数学上学期同步课件(人教A版2019必修第一册)(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 00:00:00 | ||
图片预览










文档简介
(共47张PPT)
5.5.2 简单的三角恒等变换
学习了和 ( 差 ) 角公式 、 二倍角公式以后 , 我们就有了进行三角恒等变换的新工具 ,从而使三角恒等变换的内容 、 思路和方法更加丰富 .
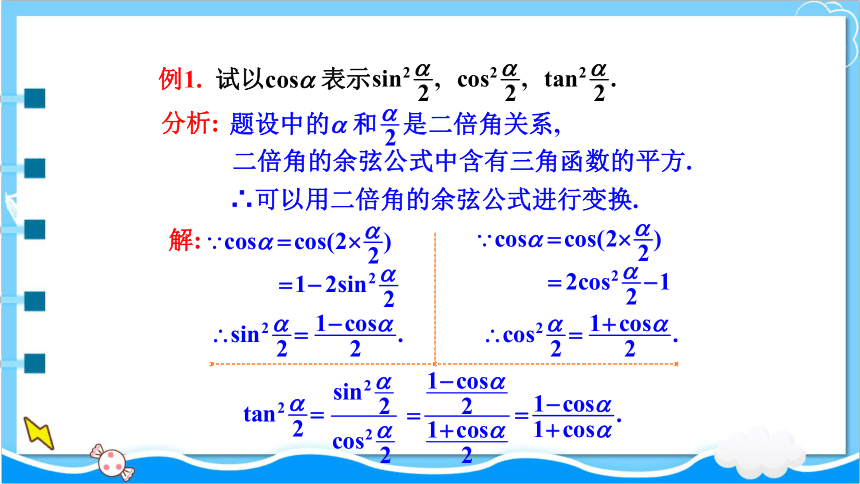
例1. 试以cosa 表示
分析:
二倍角的余弦公式中含有三角函数的平方.
∴可以用二倍角的余弦公式进行变换.
题设中的a 和 是二倍角关系,
解:
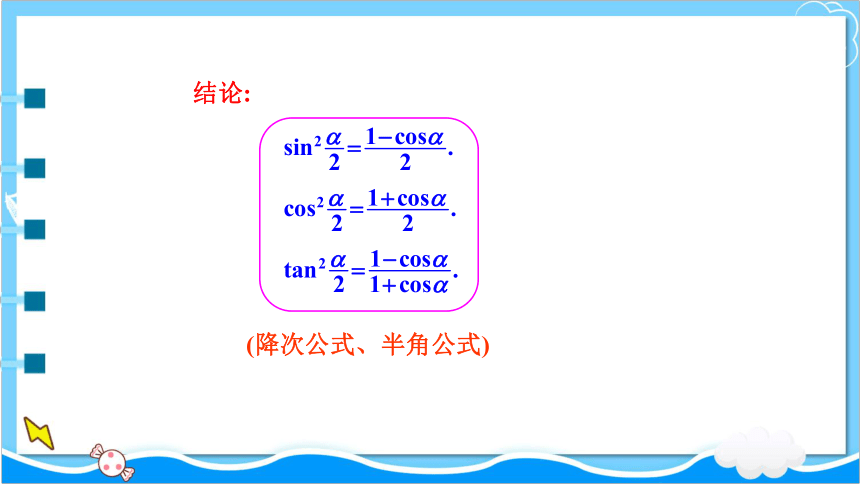
结论:
(降次公式、半角公式)
分析:
(1)
等式左边是单角a、b,
右边是和角, 差角,
可考虑用和(差)角公式从右证到左.
证明:
右边 =
= sina cosb
= 左边,
∴等式成立.
例2. 求证:
(1)
(2)
(二) 和差角公式的变换使用
例2. 求证:
(1)
(2)
分析:
(2)
仔细观察左右两边的结构形式,
于是可以根据第 (1) 题求证.
类似于2sina cosb,
类似于(1)题两边乘以 2 后的左边,
于是得到启示: 换元,
令
则 a +b =
q,
a -b =
j,
(二) 和差角公式的变换使用
证明:
(2)
令
则 a +b =q,
a -b =j,
( (1)结论 )
= 左边,
∴等式成立.
例2. 求证:
(1)
(2)
(二) 和差角公式的变换使用
补充例1.
求 cos(a -b) 的值.
分析:
将已知中的两式分别平方就有了.
∵cos(a -b) =sina sinb+cosa cosb,
考虑需要的sina sinb 和cosa cosb从哪里来,
(三) 构造变换
补充例1.
求 cos(a -b) 的值.
(三) 构造变换
将两式相加得
2-2(sina sinb+cosa cosb)
得 cos (a -b) =
解:
将已知两式分别平方得
即 2-2cos(a -b)
(构造和 (差) 角形式)
(三) 构造变换
补充例2. 求证:
分析:
等式的左边是二倍角, 右边是单角,
思想:
用二倍角公式化为单角,
问题:
cos2a 化成哪一个
不妨把右边切化弦观察,
若分子乘以cosa +sina 就得cos2a -sin2a,
即为 cos2a.
(三) 构造变换
补充例2. 求证:
证明:
左边 =
(构造完全平方)
(分子母同除以cosa)
=右边,
∴等式成立.
(三) 构造变换
补充例3. 已知A、B、C是三角形的内角, 求证: tanA+tanB+tanC = tanAtanBtanC.
分析:
将所证等式变形得,
tanA+tanB = (tanAtanB-1)tanC,
构造成了和角的正切,
-tanC 恰是 tan(A+B).
(三) 构造变换
补充例3. 已知A、B、C是三角形的内角, 求证: tanA+tanB+tanC = tanAtanBtanC.
证明:
= -tanC,
= tan(180 -C)
∴tanA+tanB = (1-tanAtanB)(-tanC)
= -tanC+tanAtanBtanC,
即得 tanA+tanB+tanC = tanAtanBtanC.
和角正切的变形应用:
tana +tanb =tan(a +b)(1-tana tanb).
例4. 求函数 y=sin x + cos x 的周期, 最大值和最小值.
分析:
要求周期、最值, 最好是把函数化成只有
一个三角函数的形式.
而函数的结构形式是 a sina + b cosa 的形式,
∴可考虑用辅助角公式.
(四) 辅助角公式化一
例4. (1) 求函数 y=sin x + cos x 的周期, 最大值和最小值.
(四) 辅助角公式化一
解(1):
∴函数的周期是2p, 最大值是2, 最小值是-2.
例4. (2) 求函数 y = 3sinx + 4cosx 的周期,最大值与最小值.
解:
(2)
y = 3sinx + 4cosx
令
则
∴函数的周期是2p, 最大值是5, 最小值是-5.
(五) 应用中的三角变换
例5. 如图, 已知OPQ是半径为 1, 圆心角为 的
扇形, C 是扇形弧上的动点, ABCD 是扇形的内接矩形. 记∠COP = a, 求当角 a 取何值时, 矩形ABCD的面积最大 并求出这个最大面积.
O
A
B
P
C
Q
D
a
分析:
矩形面积为长乘宽,
用 a 的三角函数表示长和宽, 面积则
为一个三角函数式, 由三角函数求最值.
(五) 应用中的三角变换
例4. 如图, 已知OPQ是半径为 1, 圆心角为 的扇形, C 是扇形弧上的动点, ABCD 是扇形的内接矩形. 记∠COP = a, 求当角 a 取何值时, 矩形ABCD的面积最大 并求出这个最大面积.
O
A
B
P
C
Q
D
a
解:
在Rt△OBC中, OC =1,
BC = OC·sina
在Rt△OAD中,
= sina,
OB = OC·cosa
= cosa,
OA =AD·tan
则 AB = OB-OA
∴SABCD = AB·BC
则当 时,
即a = 时,
S最大=
接上页∴SABCD = AB·BC
在三角恒等变换中, 注意以下解题思想的运用:
1. 向着同种函数转化
2. 向着同角转化
3. 向着一个三角函数转化
正、余弦的互化,
正、余切化正、余弦(切化弦).
诱导公式,
二倍角公式.
和(差)角公式(辅助角化一).
1. 求证:
证明:
(切化弦)
(分子构造二倍角正弦)
(分母构造二倍角余弦)
第一个等号证得.
当堂达标
1. 求证:
证明:
(切化弦)
(分子构造二倍角正弦)
(分母构造二倍角余弦)
第一个等号证得.
(分子母同乘 sina 使分母强构成sina)
(平方关系)
第二个等号证得.
(分解因式)
2. 求证:
(1)
(2)
(3)
证明:
(1)
∵sin(a+b) = sina cosb + cosa sinb,
sin(a-b) = sina cosb - cosa sinb,
两式相减得
sin(a+b) - sin(a-b) = 2cosa sinb,
两边除以 2 即得
2. 求证:
(1)
(2)
(3)
证明:
(2)
∵cos(a+b) = cosa cosb - sina sinb,
cos(a-b) = cosa cosb + sina sinb,
两式相加得
cos(a+b) + cos(a-b) = 2cosa cosb,
两边除以 2 即得
2. 求证:
(1)
(2)
(3)
证明:
(3)
∵cos(a+b) = cosa cosb - sina sinb,
cos(a-b) = cosa cosb + sina sinb,
两式相减得
cos(a+b) - cos(a-b) = -2sina sinb,
两边除以 -2 即得
3. 求证:
(1)
(2)
(3)
证明:
(1)
令
则
sinq - sinj = sin(a+b) - sin(a -b)
= sina cosb + cosa sinb
- (sina cosb- cosa sinb)
= 2cosa sinb
3. 求证:
(1)
(2)
(3)
证明:
(2)
令
则
cosq + cosj = cos(a+b) + cos(a -b)
= cosa cosb - sina sinb
+ cosa cosb + sina sinb)
= 2cosa cosb
3. 求证:
(1)
(2)
(3)
证明:
(3)
令
则
cosq - cosj = cos(a+b) - cos(a -b)
= cosa cosb - sina sinb
- (cosa cosb + sina sinb)
= -2sina sinb
结论:
积化和差
和差化积
(习题5.5)
8. 求证:
(1) (sin2a -cos2a)2=1-sin4a;
(2)
(3)
(4)
(5)
(6)
(习题5.5)
8. 求证:
(1) (sin2a -cos2a)2=1-sin4a;
证明:
左边 =
sin22a +cos22a -2sin2a cos2a
= 1 - sin4a
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(2)
证明:
左边 =
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(3)
证明:
左边 =
= 右边,
∴等式成立.
= cosj +sinj
(习题5.5)
8. 求证:
(4)
证明:
左边 =
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(5)
证明:
左边 =
= 右边,
∴等式成立.
= tan2q
(习题5.5)
8. 求证:
(6)
证明:
左边 =
= 右边,
∴等式成立.
= tanq
9. 已知sin(a +b) = sin(a -b) =
(1) 求证: sina cosb = 5cosa sinb;
(2) 求证: tana = 5tanb.
证明:
由
①
②
(1)
① + ②得
① - ②得
两式相除得
∴sina cosb = 5cosa sinb.
③
(2)
将③式两边同除以cosa cosb 即得
tana = 5tanb.
10. 已知 求证 tan2q = - 4tan(q + ).
证明:
由 解得
15. 求证:
(1) 3 +cos4a - 4cos2a = 8sin4a;
(2)
证明:
(1)
左边=
3+1-2sin22a-4(1-2sin2a)
= -2(2sinacosa)2+8sin2a
= -8sin2a(1-sin2a)+8sin2a
= 8sin4a
=右边.
15. 求证:
(1) 3 +cos4a - 4cos2a = 8sin4a;
(2)
证明:
(2)
左边=
=右边.
17. 求函数 f(x) = sin( +4x) + cos(4x - )的最小正周期和递减区间.
解:
最小正周期为
递减区间为
解:
在Rt△DCB中, DB = 2R,
则 DC = 2Rcosa,
BC = 2Rsina,
矩形面积 S = DC·BC
= 4R2sina cosa
= 2R2sin2a
当 2a = 90 时, S 取得最大值,
即 a = 45 , 矩形是正方形时,
S 取得最大值,
S最大= 2R2.
A
B
C
D
a
补充题. 如图, 把一段半径为R的圆木锯成横截面为矩形的木料, 当角a 为多大时矩形面积最大 并求出这个最大面积.
16. 是否存在锐角a, b, 使a +2b = tan tanb =2- 同时成立 若存在, 求出a、b 的度数; 若不存在, 请说明理由.
解:
若存在, 则
整理得
解得
或 tanb =1,
将tanb = 代入上式得
则a =90 , 不是锐角, 不合题意;
当tanb =1时,
则
即存在 使题设条件成立.
19. 你能利用右图, 给出下列两个等式的一个证明吗
x
y
o
B(cosb, sinb)
A(cosa, sina)
M
分析:
∵M是AB的中点,
∴M点的坐标为
又在Rt△OAM中, 用角 表示OM:
M
作MM ⊥x 轴于M ,
则 xM = OMcos∠MOM
yM = OMsin∠MOM
与上面点M的坐标相等, 即得所证等式.
20. 设 f(a) = sinxa +cosxa, x {n | n = 2k, k N+}.利用三角变换, 估计 f(a) 在 x = 2, 4, 6 时的取值情况, 进而对 x 取一般值时 f(a)的取值范围作出一个猜想.
分析:
当 x = 2 时, f(a) =1,
当 x = 4 时,
f(a) = sin4a+cos4a,
= (sin2a+cos2a)2-2sin2a cos2a,
= 1-2sin2a cos2a,
≤1,
当 x = 6 时,
f(a) = sin6a+cos6a,
= (sin2a+cos2a)(sin4a -sin2a cos2a + cos4a),
= 1-3sin2a cos2a,
≤1,
= (sin2a+cos2a)2-3sin2a cos2a,
≤
≤
猜想:
补充. 若sin76 =m, 试用含m的式子表示cos7 .
解:
课堂小结
5.5.2 简单的三角恒等变换
学习了和 ( 差 ) 角公式 、 二倍角公式以后 , 我们就有了进行三角恒等变换的新工具 ,从而使三角恒等变换的内容 、 思路和方法更加丰富 .
例1. 试以cosa 表示
分析:
二倍角的余弦公式中含有三角函数的平方.
∴可以用二倍角的余弦公式进行变换.
题设中的a 和 是二倍角关系,
解:
结论:
(降次公式、半角公式)
分析:
(1)
等式左边是单角a、b,
右边是和角, 差角,
可考虑用和(差)角公式从右证到左.
证明:
右边 =
= sina cosb
= 左边,
∴等式成立.
例2. 求证:
(1)
(2)
(二) 和差角公式的变换使用
例2. 求证:
(1)
(2)
分析:
(2)
仔细观察左右两边的结构形式,
于是可以根据第 (1) 题求证.
类似于2sina cosb,
类似于(1)题两边乘以 2 后的左边,
于是得到启示: 换元,
令
则 a +b =
q,
a -b =
j,
(二) 和差角公式的变换使用
证明:
(2)
令
则 a +b =q,
a -b =j,
( (1)结论 )
= 左边,
∴等式成立.
例2. 求证:
(1)
(2)
(二) 和差角公式的变换使用
补充例1.
求 cos(a -b) 的值.
分析:
将已知中的两式分别平方就有了.
∵cos(a -b) =sina sinb+cosa cosb,
考虑需要的sina sinb 和cosa cosb从哪里来,
(三) 构造变换
补充例1.
求 cos(a -b) 的值.
(三) 构造变换
将两式相加得
2-2(sina sinb+cosa cosb)
得 cos (a -b) =
解:
将已知两式分别平方得
即 2-2cos(a -b)
(构造和 (差) 角形式)
(三) 构造变换
补充例2. 求证:
分析:
等式的左边是二倍角, 右边是单角,
思想:
用二倍角公式化为单角,
问题:
cos2a 化成哪一个
不妨把右边切化弦观察,
若分子乘以cosa +sina 就得cos2a -sin2a,
即为 cos2a.
(三) 构造变换
补充例2. 求证:
证明:
左边 =
(构造完全平方)
(分子母同除以cosa)
=右边,
∴等式成立.
(三) 构造变换
补充例3. 已知A、B、C是三角形的内角, 求证: tanA+tanB+tanC = tanAtanBtanC.
分析:
将所证等式变形得,
tanA+tanB = (tanAtanB-1)tanC,
构造成了和角的正切,
-tanC 恰是 tan(A+B).
(三) 构造变换
补充例3. 已知A、B、C是三角形的内角, 求证: tanA+tanB+tanC = tanAtanBtanC.
证明:
= -tanC,
= tan(180 -C)
∴tanA+tanB = (1-tanAtanB)(-tanC)
= -tanC+tanAtanBtanC,
即得 tanA+tanB+tanC = tanAtanBtanC.
和角正切的变形应用:
tana +tanb =tan(a +b)(1-tana tanb).
例4. 求函数 y=sin x + cos x 的周期, 最大值和最小值.
分析:
要求周期、最值, 最好是把函数化成只有
一个三角函数的形式.
而函数的结构形式是 a sina + b cosa 的形式,
∴可考虑用辅助角公式.
(四) 辅助角公式化一
例4. (1) 求函数 y=sin x + cos x 的周期, 最大值和最小值.
(四) 辅助角公式化一
解(1):
∴函数的周期是2p, 最大值是2, 最小值是-2.
例4. (2) 求函数 y = 3sinx + 4cosx 的周期,最大值与最小值.
解:
(2)
y = 3sinx + 4cosx
令
则
∴函数的周期是2p, 最大值是5, 最小值是-5.
(五) 应用中的三角变换
例5. 如图, 已知OPQ是半径为 1, 圆心角为 的
扇形, C 是扇形弧上的动点, ABCD 是扇形的内接矩形. 记∠COP = a, 求当角 a 取何值时, 矩形ABCD的面积最大 并求出这个最大面积.
O
A
B
P
C
Q
D
a
分析:
矩形面积为长乘宽,
用 a 的三角函数表示长和宽, 面积则
为一个三角函数式, 由三角函数求最值.
(五) 应用中的三角变换
例4. 如图, 已知OPQ是半径为 1, 圆心角为 的扇形, C 是扇形弧上的动点, ABCD 是扇形的内接矩形. 记∠COP = a, 求当角 a 取何值时, 矩形ABCD的面积最大 并求出这个最大面积.
O
A
B
P
C
Q
D
a
解:
在Rt△OBC中, OC =1,
BC = OC·sina
在Rt△OAD中,
= sina,
OB = OC·cosa
= cosa,
OA =AD·tan
则 AB = OB-OA
∴SABCD = AB·BC
则当 时,
即a = 时,
S最大=
接上页∴SABCD = AB·BC
在三角恒等变换中, 注意以下解题思想的运用:
1. 向着同种函数转化
2. 向着同角转化
3. 向着一个三角函数转化
正、余弦的互化,
正、余切化正、余弦(切化弦).
诱导公式,
二倍角公式.
和(差)角公式(辅助角化一).
1. 求证:
证明:
(切化弦)
(分子构造二倍角正弦)
(分母构造二倍角余弦)
第一个等号证得.
当堂达标
1. 求证:
证明:
(切化弦)
(分子构造二倍角正弦)
(分母构造二倍角余弦)
第一个等号证得.
(分子母同乘 sina 使分母强构成sina)
(平方关系)
第二个等号证得.
(分解因式)
2. 求证:
(1)
(2)
(3)
证明:
(1)
∵sin(a+b) = sina cosb + cosa sinb,
sin(a-b) = sina cosb - cosa sinb,
两式相减得
sin(a+b) - sin(a-b) = 2cosa sinb,
两边除以 2 即得
2. 求证:
(1)
(2)
(3)
证明:
(2)
∵cos(a+b) = cosa cosb - sina sinb,
cos(a-b) = cosa cosb + sina sinb,
两式相加得
cos(a+b) + cos(a-b) = 2cosa cosb,
两边除以 2 即得
2. 求证:
(1)
(2)
(3)
证明:
(3)
∵cos(a+b) = cosa cosb - sina sinb,
cos(a-b) = cosa cosb + sina sinb,
两式相减得
cos(a+b) - cos(a-b) = -2sina sinb,
两边除以 -2 即得
3. 求证:
(1)
(2)
(3)
证明:
(1)
令
则
sinq - sinj = sin(a+b) - sin(a -b)
= sina cosb + cosa sinb
- (sina cosb- cosa sinb)
= 2cosa sinb
3. 求证:
(1)
(2)
(3)
证明:
(2)
令
则
cosq + cosj = cos(a+b) + cos(a -b)
= cosa cosb - sina sinb
+ cosa cosb + sina sinb)
= 2cosa cosb
3. 求证:
(1)
(2)
(3)
证明:
(3)
令
则
cosq - cosj = cos(a+b) - cos(a -b)
= cosa cosb - sina sinb
- (cosa cosb + sina sinb)
= -2sina sinb
结论:
积化和差
和差化积
(习题5.5)
8. 求证:
(1) (sin2a -cos2a)2=1-sin4a;
(2)
(3)
(4)
(5)
(6)
(习题5.5)
8. 求证:
(1) (sin2a -cos2a)2=1-sin4a;
证明:
左边 =
sin22a +cos22a -2sin2a cos2a
= 1 - sin4a
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(2)
证明:
左边 =
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(3)
证明:
左边 =
= 右边,
∴等式成立.
= cosj +sinj
(习题5.5)
8. 求证:
(4)
证明:
左边 =
= 右边,
∴等式成立.
(习题5.5)
8. 求证:
(5)
证明:
左边 =
= 右边,
∴等式成立.
= tan2q
(习题5.5)
8. 求证:
(6)
证明:
左边 =
= 右边,
∴等式成立.
= tanq
9. 已知sin(a +b) = sin(a -b) =
(1) 求证: sina cosb = 5cosa sinb;
(2) 求证: tana = 5tanb.
证明:
由
①
②
(1)
① + ②得
① - ②得
两式相除得
∴sina cosb = 5cosa sinb.
③
(2)
将③式两边同除以cosa cosb 即得
tana = 5tanb.
10. 已知 求证 tan2q = - 4tan(q + ).
证明:
由 解得
15. 求证:
(1) 3 +cos4a - 4cos2a = 8sin4a;
(2)
证明:
(1)
左边=
3+1-2sin22a-4(1-2sin2a)
= -2(2sinacosa)2+8sin2a
= -8sin2a(1-sin2a)+8sin2a
= 8sin4a
=右边.
15. 求证:
(1) 3 +cos4a - 4cos2a = 8sin4a;
(2)
证明:
(2)
左边=
=右边.
17. 求函数 f(x) = sin( +4x) + cos(4x - )的最小正周期和递减区间.
解:
最小正周期为
递减区间为
解:
在Rt△DCB中, DB = 2R,
则 DC = 2Rcosa,
BC = 2Rsina,
矩形面积 S = DC·BC
= 4R2sina cosa
= 2R2sin2a
当 2a = 90 时, S 取得最大值,
即 a = 45 , 矩形是正方形时,
S 取得最大值,
S最大= 2R2.
A
B
C
D
a
补充题. 如图, 把一段半径为R的圆木锯成横截面为矩形的木料, 当角a 为多大时矩形面积最大 并求出这个最大面积.
16. 是否存在锐角a, b, 使a +2b = tan tanb =2- 同时成立 若存在, 求出a、b 的度数; 若不存在, 请说明理由.
解:
若存在, 则
整理得
解得
或 tanb =1,
将tanb = 代入上式得
则a =90 , 不是锐角, 不合题意;
当tanb =1时,
则
即存在 使题设条件成立.
19. 你能利用右图, 给出下列两个等式的一个证明吗
x
y
o
B(cosb, sinb)
A(cosa, sina)
M
分析:
∵M是AB的中点,
∴M点的坐标为
又在Rt△OAM中, 用角 表示OM:
M
作MM ⊥x 轴于M ,
则 xM = OMcos∠MOM
yM = OMsin∠MOM
与上面点M的坐标相等, 即得所证等式.
20. 设 f(a) = sinxa +cosxa, x {n | n = 2k, k N+}.利用三角变换, 估计 f(a) 在 x = 2, 4, 6 时的取值情况, 进而对 x 取一般值时 f(a)的取值范围作出一个猜想.
分析:
当 x = 2 时, f(a) =1,
当 x = 4 时,
f(a) = sin4a+cos4a,
= (sin2a+cos2a)2-2sin2a cos2a,
= 1-2sin2a cos2a,
≤1,
当 x = 6 时,
f(a) = sin6a+cos6a,
= (sin2a+cos2a)(sin4a -sin2a cos2a + cos4a),
= 1-3sin2a cos2a,
≤1,
= (sin2a+cos2a)2-3sin2a cos2a,
≤
≤
猜想:
补充. 若sin76 =m, 试用含m的式子表示cos7 .
解:
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
