3.1.1两角差的余弦公式教学课件-2021-2022学年高一上学期数学人教A版必修4(共17张PPT)
文档属性
| 名称 | 3.1.1两角差的余弦公式教学课件-2021-2022学年高一上学期数学人教A版必修4(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 15:26:00 | ||
图片预览





文档简介
(共17张PPT)
人教A版必修4
3.1.1两角差的余弦公式
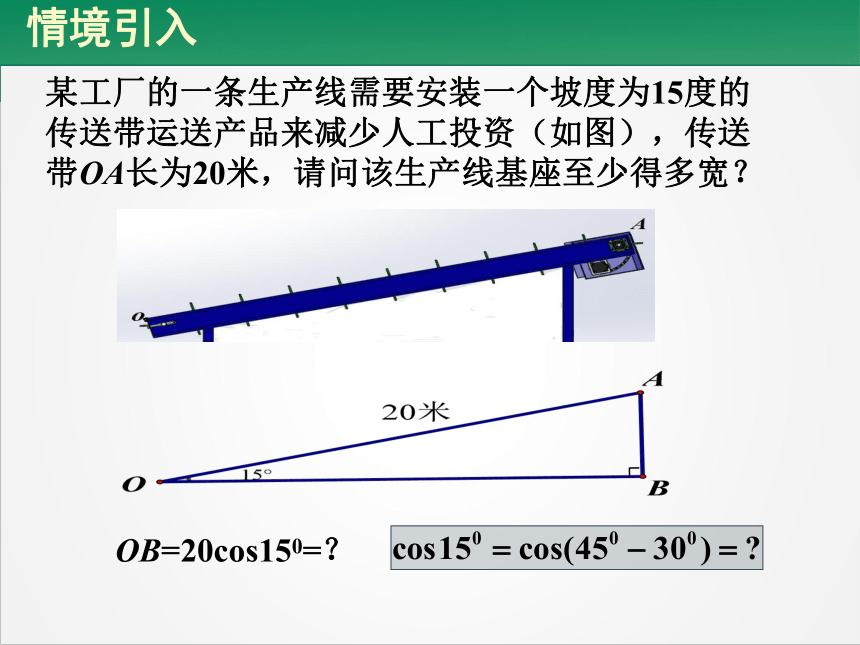
情境引入
OB=20cos150=?
某工厂的一条生产线需要安装一个坡度为15度的传送带运送产品来减少人工投资(如图),传送带OA长为20米,请问该生产线基座至少得多宽?
问题提出
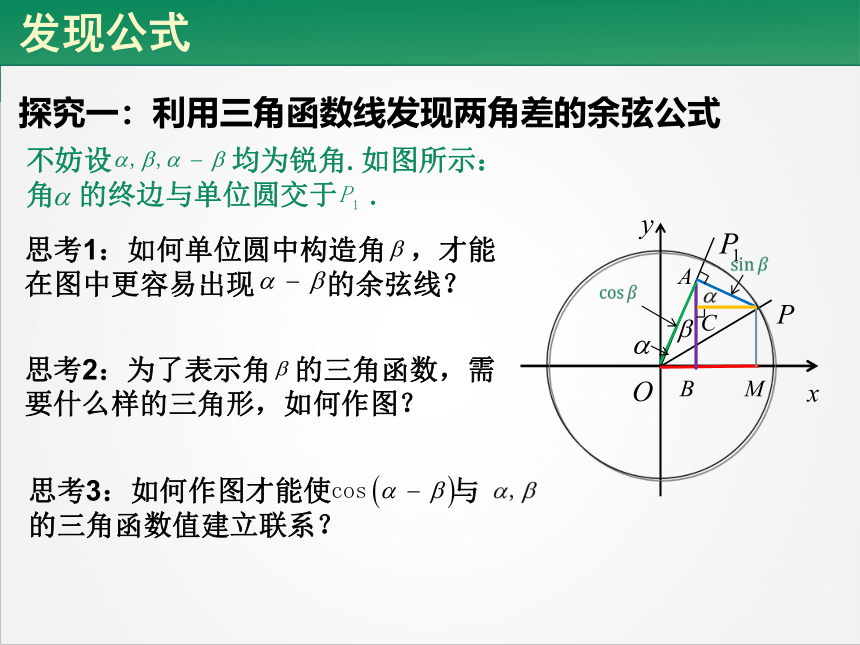
探究一:利用三角函数线发现两角差的余弦公式
发现公式
思考1:如何单位圆中构造角 ,才能在图中更容易出现 的余弦线?
思考2:为了表示角 的三角函数,需要什么样的三角形,如何作图?
思考3:如何作图才能使 与
的三角函数值建立联系?
不妨设 均为锐角.如图所示:
角 的终边与单位圆交于 .
思考
思考:我们能够运用其他的方法来证明两角差的余弦公式吗?
证明公式
x1 x2+y1 y2
向量的数量积
探究二:向量法推导两角差的余弦公式
小组思考与讨论:
1.根据分析,如何确定向量数量积运算中的两个向
量 、 ?
2.怎样利用向量的数量积的计算公式得到探究结果?
证明公式
θ
探究二:向量法推导两角差的余弦公式
B(cos β,sin β)
A(cos α,sin α)
θ
θ
证明公式
两角差的余弦公式
C(α-β):cos(α-β)=cos αcos β+sin αsin β.
公式的特征
思考:两角差的余弦公式有什么特征?
(1)适用条件:公式中的角 都是任意角.
(2)公式结构:公式左边是两角差的余弦,公式右端的两部分为同名三角函数的积,连接符号与左边角的连接符号相反.
数学史
三角函数弦表
两千多年前亚历山大的数学家希帕霍斯 (Hipparhcsu ) 利用相当于三角函数和差角公式的结果制作了目前所知的第一个弦表, 可惜未能流传下来。后来托勒密也利用相当于和差角公式 , 制成现存最早的三角函数的弦表, 弦表在后来的天体测量与测量中有着非常重要的应用。
数学史
古埃及天文学家托勒密在三角函数弦表中的方法如图1,公元3世纪亚历山大数学家帕普斯《数学汇编》中给出的证法如图2.
图1.三角函数弦表
图2.《数学汇编》
拓展思考 三角形面积推导两角差的余弦公式
中国科学院张景中先生从上世纪80年代就开始研究用面积法解决几何证明问题,进而形成了几何学中的新体系,并创造了几何定理机器证明的“消点法”,下面我们就从三角形面积出发进行证明.
课后思考:我们能够通过如上图来推导两角差的余弦
公式吗?
1.某工厂的一条生产线需要安装一个坡度为15度的传送带运送产品来减少人工投资(如图),传送带OA长为20米,请问该生产线基座至少得多宽?
巩固应用
巩固应用
2
回顾小结
思考:通过本节课的学习,我们学习了哪些数学知识;在探究的过程中,又蕴含着哪些数学思想呢?
回顾小结
1.数学知识:两角差的余弦公式以及对公式的运用
2.数学方法:数形结合,特殊到一般、转化与化归等.
作业
(2)运用课堂上所提的面积法及图形,推导两角差的余弦公式;
(3)通过查阅相关资料,自主研究公式的其他推导方法.
2.思考:
(1) 用“三角函数线”发现两角差的余弦公式过程中将角推广到任意角的情形;
1.课本P137习题A组第2,3题;
人教A版必修4
3.1.1两角差的余弦公式
情境引入
OB=20cos150=?
某工厂的一条生产线需要安装一个坡度为15度的传送带运送产品来减少人工投资(如图),传送带OA长为20米,请问该生产线基座至少得多宽?
问题提出
探究一:利用三角函数线发现两角差的余弦公式
发现公式
思考1:如何单位圆中构造角 ,才能在图中更容易出现 的余弦线?
思考2:为了表示角 的三角函数,需要什么样的三角形,如何作图?
思考3:如何作图才能使 与
的三角函数值建立联系?
不妨设 均为锐角.如图所示:
角 的终边与单位圆交于 .
思考
思考:我们能够运用其他的方法来证明两角差的余弦公式吗?
证明公式
x1 x2+y1 y2
向量的数量积
探究二:向量法推导两角差的余弦公式
小组思考与讨论:
1.根据分析,如何确定向量数量积运算中的两个向
量 、 ?
2.怎样利用向量的数量积的计算公式得到探究结果?
证明公式
θ
探究二:向量法推导两角差的余弦公式
B(cos β,sin β)
A(cos α,sin α)
θ
θ
证明公式
两角差的余弦公式
C(α-β):cos(α-β)=cos αcos β+sin αsin β.
公式的特征
思考:两角差的余弦公式有什么特征?
(1)适用条件:公式中的角 都是任意角.
(2)公式结构:公式左边是两角差的余弦,公式右端的两部分为同名三角函数的积,连接符号与左边角的连接符号相反.
数学史
三角函数弦表
两千多年前亚历山大的数学家希帕霍斯 (Hipparhcsu ) 利用相当于三角函数和差角公式的结果制作了目前所知的第一个弦表, 可惜未能流传下来。后来托勒密也利用相当于和差角公式 , 制成现存最早的三角函数的弦表, 弦表在后来的天体测量与测量中有着非常重要的应用。
数学史
古埃及天文学家托勒密在三角函数弦表中的方法如图1,公元3世纪亚历山大数学家帕普斯《数学汇编》中给出的证法如图2.
图1.三角函数弦表
图2.《数学汇编》
拓展思考 三角形面积推导两角差的余弦公式
中国科学院张景中先生从上世纪80年代就开始研究用面积法解决几何证明问题,进而形成了几何学中的新体系,并创造了几何定理机器证明的“消点法”,下面我们就从三角形面积出发进行证明.
课后思考:我们能够通过如上图来推导两角差的余弦
公式吗?
1.某工厂的一条生产线需要安装一个坡度为15度的传送带运送产品来减少人工投资(如图),传送带OA长为20米,请问该生产线基座至少得多宽?
巩固应用
巩固应用
2
回顾小结
思考:通过本节课的学习,我们学习了哪些数学知识;在探究的过程中,又蕴含着哪些数学思想呢?
回顾小结
1.数学知识:两角差的余弦公式以及对公式的运用
2.数学方法:数形结合,特殊到一般、转化与化归等.
作业
(2)运用课堂上所提的面积法及图形,推导两角差的余弦公式;
(3)通过查阅相关资料,自主研究公式的其他推导方法.
2.思考:
(1) 用“三角函数线”发现两角差的余弦公式过程中将角推广到任意角的情形;
1.课本P137习题A组第2,3题;
