探究刻画椭圆扁平程度的数学模型 课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共24张PPT)
文档属性
| 名称 | 探究刻画椭圆扁平程度的数学模型 课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 15:18:42 | ||
图片预览






文档简介
(共24张PPT)
探究刻画椭圆扁平程度的数学模型
人民教育出版社 A版 选择性必修第一册
教学内容解析
学生学情分析
教学策略分析
教学目标设置
C
ontents
目录
教学过程与反思
1
教学内容解析
★第一单元 椭圆
(共4课时)
分讲1(1课时)探究椭圆的概念与方程的推导
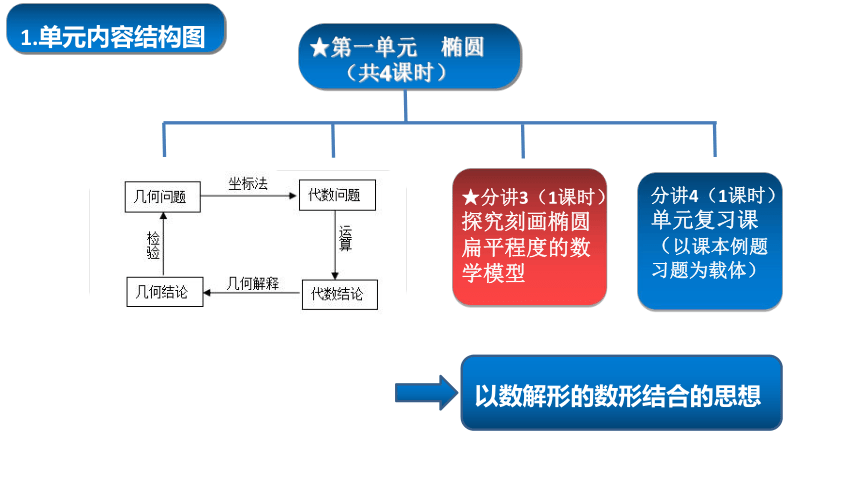
1.单元内容结构图
分讲2(1课时)
复习椭圆方程,探究椭圆简单的几何性质1
★分讲3(1课时)探究刻画椭圆扁平程度的数学模型
分讲4(1课时)
单元复习课(以课本例题习题为载体)
以数解形的数形结合的思想
教学内容解析
教学策略分析
教学过程设计
学生学情分析
教学目标设置
课时内容
要探究学习:
1.用数量关系探究刻画椭圆扁平程度的数学模型.
2.从实物的观察与实验,代数的运算等过程探究,体验数学抽象的核心素养.
3.通过实验控制变量的探究过程体验多元转化一元的数学思想.
教学重点
探究刻画椭圆扁平程度的数学模型
学生学情分析
2
教学目标设置
01
02
02
01
教学目标
达成目标的标志
通过画图,观察联想,数学运算,实验解释等过程,探究刻画椭圆扁平程度的数学模型,体验数学建模的核心素养.
能按照数学建模的路径去刻画椭圆的扁平程度,即发现与提出问题,拟定计划,建立模型,完善模型,模型运用.
能用代数运算解释几何问题,并通过控制变量的手段实验发现规律,并通过实验结果找出多种代数的合理解释理由,完善模型,能感受到数的运算能发现形,形的特征能说明数的合理性的数形结合的思想.
教学目标设置
教学内容解析
教学策略分析
教学过程设计
学生学情分析
通过观察和动手画图实验,数学运算等探究过程,理解”以数解形的数形结合思想,提高学生直观想象和逻辑推理的能力.
3
学生学情分析
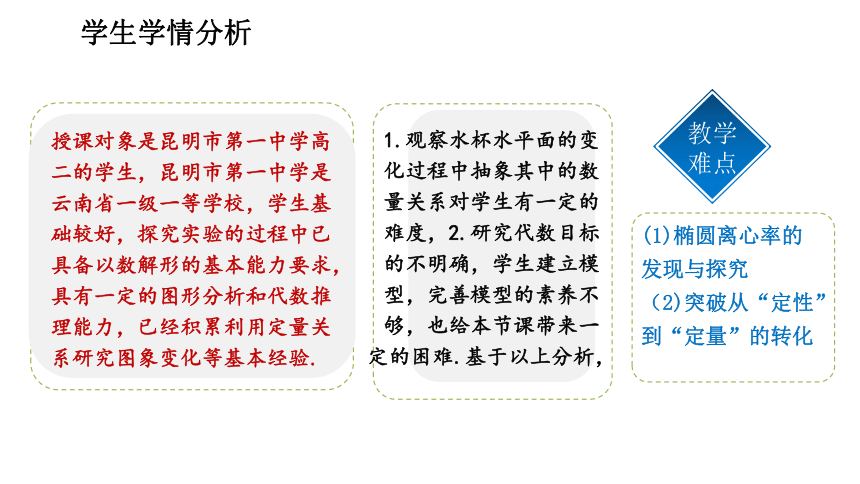
学生学情分析
授课对象是昆明市第一中学高二的学生,昆明市第一中学是云南省一级一等学校,学生基础较好,探究实验的过程中已具备以数解形的基本能力要求,具有一定的图形分析和代数推理能力,已经积累利用定量关系研究图象变化等基本经验.
1.观察水杯水平面的变化过程中抽象其中的数量关系对学生有一定的难度,2.研究代数目标的不明确,学生建立模型,完善模型的素养不够,也给本节课带来一定的困难.基于以上分析,
教学难点
(1)椭圆离心率的发现与探究
(2)突破从“定性”到“定量”的转化
4
教学策略分析
教学内容解析
教学过程设计
学生学情分析
教学目标设置
教学策略分析
问题驱动
利用问题串引导学生对知识进行探究。
教法:演示教学
学生利用工具观察水杯和画出不同椭圆,并体会离心率对椭圆形状的影响,有效突破本节课难点。
信息技术融合
利用画板等多种技术动态演示
本着“以学生为主体,教师为主导”的理念设计以下的如下策略:
学法:合作探究
重难点知识采用小组合作探究的方式,学生学会合作的同时,突破难点。当堂展示,提升学生表达能力
5
教学过程与反思
环节一:呈现生活情境,发现与提出问题
环节二:观察联想,探寻研究路径
环节三:探究分析,建立模型
环节四:逻辑推理,完善模型
环节五:模型应用,提升能力
环节六:回顾反思,归纳总结
教学过程
生活情境
创设情境
设计意图
让学生直观观察发现椭圆存在扁平程度不一的情况,也让学生感受椭圆的扁平在生活也随处可见,让学生感受到构建刻画椭圆扁平程度模型的必要性.
第一环节——呈现生活情境,发现与提出问题
教学过程
数学情境
发现与提出问题
教学过程
这是本节课第一次以数解形的过程,通过问题串的方式驱动,让知识发生更加自然,也让学生的自理解过程也很自然,两个“自然的过程”更好的统一,也让数学的探究更有味道.
第二环节——观察联想,探寻研究路径
设计意图
教学过程
第二次让学生体验到以数解形的数形结合的思想,让学生体验数学模型中的研究对象可以从特殊(具体)到一般的研究思路,培养学生的数学建模的思路,让学生在运算中找出规律并通过画图的手段来验证,培养学生的直观想象的素养和数学建模的素养.
第三环节——探究分析,建立模型
设计意图
教学过程
通过观察水杯的实验,找出其中的数量关系,让控制变量引入更加自然,更好的体现多元转化一元的思想,本环节也是第三次具体体现以数解形的数形结合思想的过程,更自然的解释模型的合理性.
第四环节——逻辑推理,完善模型
设计意图
1:观察水杯实验角度,解释模型
2:动手画图实验角度,解释模型
3:生成概念,完善模型
教学过程
整个过程有6种方案来体验控制变量,课堂上学生探究实验了其中的5种,小组展示交流了3种,由于本质是一样的,视频展示其中的一个片段.
第四环节——逻辑推理,完善模型
展示说明
教学过程
第四环节——逻辑推理,完善模型
设计意图:让学生利用控制变量的手段动手画图来验证模型的合理性,加深对模型的理解,第4次以数解形的数形结合思想的体现,更好的完善模型
1:观察水杯实验
2:动手画图实验
3:生成概念,完善模型
教学过程
为了让概念的生成更加自然,设计了三个问题,并尝试运用极限的语言来刻画,并通过图形的形状理解记忆离心率刻画椭圆扁平程度的结论.
第四环节——逻辑推理,完善模型
设计意图
1
1
2
3
生成概念
为什么要选择 来刻画椭圆的扁平程度
为什么叫离心率,而不叫扁平率
离心率范围的记忆方法
1:观察水杯实验
2:动手画图实验
3:生成概念,完善模型
教学过程
加深对离心率的理解,巩固概念,体验模型的应用价值,同时也是第5次具体的体现以数解形的数形结合的思想过程,更好的完成教学目标,落实核心素养.
第五环节——模型应用,提升能力
设计意图
1
教学过程
第六环节——回顾反思,归纳总结
1
从目标评价的角度出发给出两条路径让学生具体化,更好的落实目标.
把重点和难点内容整理与梳理,学生和老师共同回顾、梳理、总结本节课所学的数学知识、思想、方法,培养学生数学交流和表达的能力,让学生看到数学在刻画现实世界中的作用,体会类比与数形结合的数学思想,增强探究意识,提升学生探模建模用模能力.
设计意图
教学目标检测设计与教学反思
教学反思
1: 5次以数解形的过程让学生体验数学结合的思想,培养学生的直观想象的核心素养.
2: 通过观察水杯的实验过程中获取数学抽象的体验,
通过活动探究1,3的数量运算,培养学生的逻辑推理的能力,体验研究问题从特殊到一般的规律.
3.在建模的过程中,深化建模的路径和对知识的理解与应用,培养学生用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界.
加深对数学建模过程的体会.
感谢聆听 敬请指导
探究刻画椭圆扁平程度的数学模型
人民教育出版社 A版 选择性必修第一册
教学内容解析
学生学情分析
教学策略分析
教学目标设置
C
ontents
目录
教学过程与反思
1
教学内容解析
★第一单元 椭圆
(共4课时)
分讲1(1课时)探究椭圆的概念与方程的推导
1.单元内容结构图
分讲2(1课时)
复习椭圆方程,探究椭圆简单的几何性质1
★分讲3(1课时)探究刻画椭圆扁平程度的数学模型
分讲4(1课时)
单元复习课(以课本例题习题为载体)
以数解形的数形结合的思想
教学内容解析
教学策略分析
教学过程设计
学生学情分析
教学目标设置
课时内容
要探究学习:
1.用数量关系探究刻画椭圆扁平程度的数学模型.
2.从实物的观察与实验,代数的运算等过程探究,体验数学抽象的核心素养.
3.通过实验控制变量的探究过程体验多元转化一元的数学思想.
教学重点
探究刻画椭圆扁平程度的数学模型
学生学情分析
2
教学目标设置
01
02
02
01
教学目标
达成目标的标志
通过画图,观察联想,数学运算,实验解释等过程,探究刻画椭圆扁平程度的数学模型,体验数学建模的核心素养.
能按照数学建模的路径去刻画椭圆的扁平程度,即发现与提出问题,拟定计划,建立模型,完善模型,模型运用.
能用代数运算解释几何问题,并通过控制变量的手段实验发现规律,并通过实验结果找出多种代数的合理解释理由,完善模型,能感受到数的运算能发现形,形的特征能说明数的合理性的数形结合的思想.
教学目标设置
教学内容解析
教学策略分析
教学过程设计
学生学情分析
通过观察和动手画图实验,数学运算等探究过程,理解”以数解形的数形结合思想,提高学生直观想象和逻辑推理的能力.
3
学生学情分析
学生学情分析
授课对象是昆明市第一中学高二的学生,昆明市第一中学是云南省一级一等学校,学生基础较好,探究实验的过程中已具备以数解形的基本能力要求,具有一定的图形分析和代数推理能力,已经积累利用定量关系研究图象变化等基本经验.
1.观察水杯水平面的变化过程中抽象其中的数量关系对学生有一定的难度,2.研究代数目标的不明确,学生建立模型,完善模型的素养不够,也给本节课带来一定的困难.基于以上分析,
教学难点
(1)椭圆离心率的发现与探究
(2)突破从“定性”到“定量”的转化
4
教学策略分析
教学内容解析
教学过程设计
学生学情分析
教学目标设置
教学策略分析
问题驱动
利用问题串引导学生对知识进行探究。
教法:演示教学
学生利用工具观察水杯和画出不同椭圆,并体会离心率对椭圆形状的影响,有效突破本节课难点。
信息技术融合
利用画板等多种技术动态演示
本着“以学生为主体,教师为主导”的理念设计以下的如下策略:
学法:合作探究
重难点知识采用小组合作探究的方式,学生学会合作的同时,突破难点。当堂展示,提升学生表达能力
5
教学过程与反思
环节一:呈现生活情境,发现与提出问题
环节二:观察联想,探寻研究路径
环节三:探究分析,建立模型
环节四:逻辑推理,完善模型
环节五:模型应用,提升能力
环节六:回顾反思,归纳总结
教学过程
生活情境
创设情境
设计意图
让学生直观观察发现椭圆存在扁平程度不一的情况,也让学生感受椭圆的扁平在生活也随处可见,让学生感受到构建刻画椭圆扁平程度模型的必要性.
第一环节——呈现生活情境,发现与提出问题
教学过程
数学情境
发现与提出问题
教学过程
这是本节课第一次以数解形的过程,通过问题串的方式驱动,让知识发生更加自然,也让学生的自理解过程也很自然,两个“自然的过程”更好的统一,也让数学的探究更有味道.
第二环节——观察联想,探寻研究路径
设计意图
教学过程
第二次让学生体验到以数解形的数形结合的思想,让学生体验数学模型中的研究对象可以从特殊(具体)到一般的研究思路,培养学生的数学建模的思路,让学生在运算中找出规律并通过画图的手段来验证,培养学生的直观想象的素养和数学建模的素养.
第三环节——探究分析,建立模型
设计意图
教学过程
通过观察水杯的实验,找出其中的数量关系,让控制变量引入更加自然,更好的体现多元转化一元的思想,本环节也是第三次具体体现以数解形的数形结合思想的过程,更自然的解释模型的合理性.
第四环节——逻辑推理,完善模型
设计意图
1:观察水杯实验角度,解释模型
2:动手画图实验角度,解释模型
3:生成概念,完善模型
教学过程
整个过程有6种方案来体验控制变量,课堂上学生探究实验了其中的5种,小组展示交流了3种,由于本质是一样的,视频展示其中的一个片段.
第四环节——逻辑推理,完善模型
展示说明
教学过程
第四环节——逻辑推理,完善模型
设计意图:让学生利用控制变量的手段动手画图来验证模型的合理性,加深对模型的理解,第4次以数解形的数形结合思想的体现,更好的完善模型
1:观察水杯实验
2:动手画图实验
3:生成概念,完善模型
教学过程
为了让概念的生成更加自然,设计了三个问题,并尝试运用极限的语言来刻画,并通过图形的形状理解记忆离心率刻画椭圆扁平程度的结论.
第四环节——逻辑推理,完善模型
设计意图
1
1
2
3
生成概念
为什么要选择 来刻画椭圆的扁平程度
为什么叫离心率,而不叫扁平率
离心率范围的记忆方法
1:观察水杯实验
2:动手画图实验
3:生成概念,完善模型
教学过程
加深对离心率的理解,巩固概念,体验模型的应用价值,同时也是第5次具体的体现以数解形的数形结合的思想过程,更好的完成教学目标,落实核心素养.
第五环节——模型应用,提升能力
设计意图
1
教学过程
第六环节——回顾反思,归纳总结
1
从目标评价的角度出发给出两条路径让学生具体化,更好的落实目标.
把重点和难点内容整理与梳理,学生和老师共同回顾、梳理、总结本节课所学的数学知识、思想、方法,培养学生数学交流和表达的能力,让学生看到数学在刻画现实世界中的作用,体会类比与数形结合的数学思想,增强探究意识,提升学生探模建模用模能力.
设计意图
教学目标检测设计与教学反思
教学反思
1: 5次以数解形的过程让学生体验数学结合的思想,培养学生的直观想象的核心素养.
2: 通过观察水杯的实验过程中获取数学抽象的体验,
通过活动探究1,3的数量运算,培养学生的逻辑推理的能力,体验研究问题从特殊到一般的规律.
3.在建模的过程中,深化建模的路径和对知识的理解与应用,培养学生用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界.
加深对数学建模过程的体会.
感谢聆听 敬请指导
