2.2.2对数函数及其性质说课 课件-2021-2022学年高一上学期数学人教A版必修1(共27张PPT)
文档属性
| 名称 | 2.2.2对数函数及其性质说课 课件-2021-2022学年高一上学期数学人教A版必修1(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 15:28:21 | ||
图片预览





文档简介
(共27张PPT)
2.2.2 对数函数及其性质(1)
高中数学必修1
说 课 程 序
教学内容分析
1
教学目标设置
2
学 情 分 析
3
教学策略分析
4
教学过程分析
5
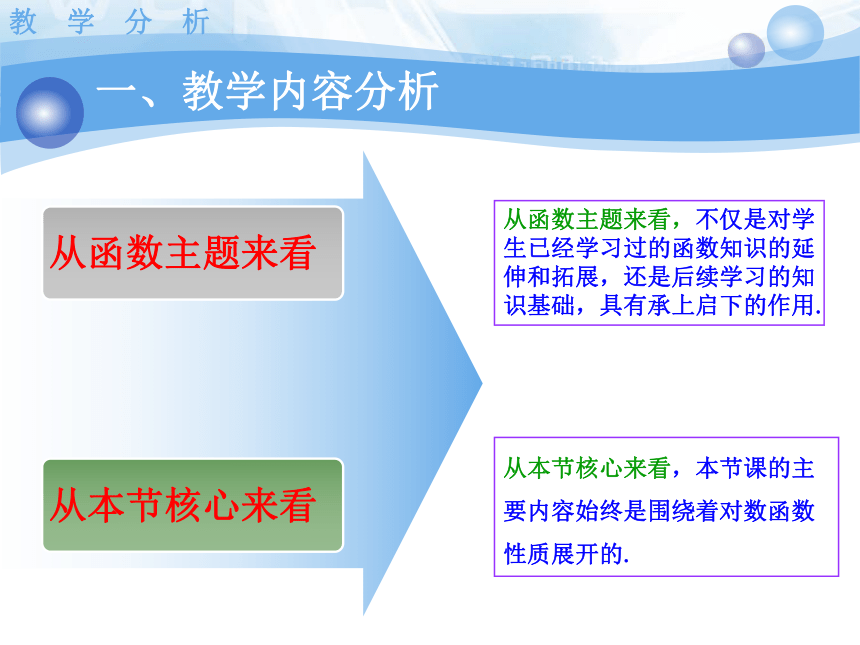
一、教学内容分析
从函数主题来看
从本节核心来看
从函数主题来看,不仅是对学生已经学习过的函数知识的延伸和拓展,还是后续学习的知识基础,具有承上启下的作用.
教 学 分 析
从本节核心来看,本节课的主要内容始终是围绕着对数函数性质展开的.
教 学 分 析
教学难点:探索对数函数性质
突出重点的方法:类比指数函数的研究过程,交流、共同确认研究对数函数的内容和方法,设计具体的操作方案,并进行具体实践操作,从中体会获得对数函数性质的方法,进一步积累研究经验.
一、教学内容分析
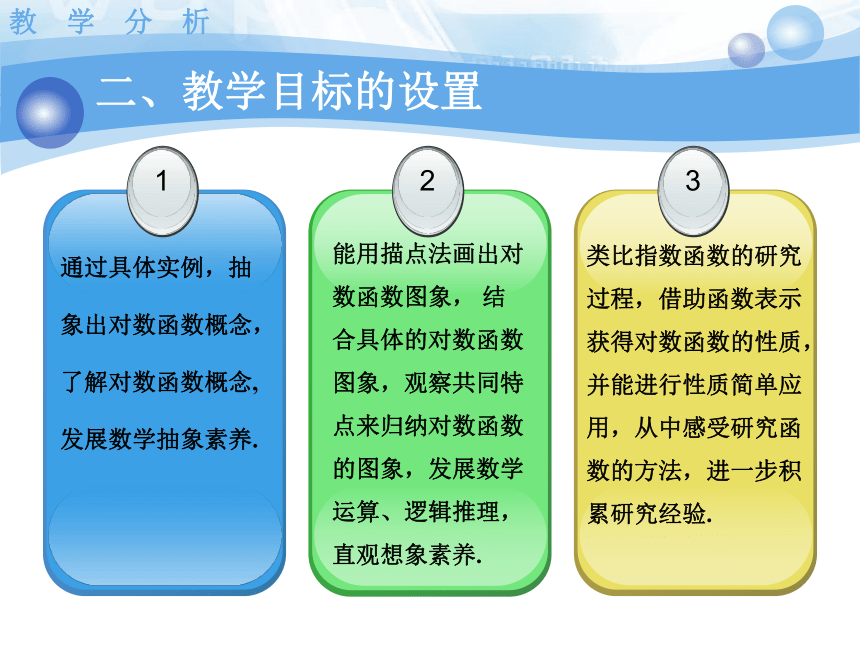
二、教学目标的设置
教 学 分 析
1
通过具体实例,抽象出对数函数概念,了解对数函数概念,发展数学抽象素养.
2
能用描点法画出对数函数图象, 结合具体的对数函数图象,观察共同特点来归纳对数函数的图象,发展数学运算、逻辑推理,直观想象素养.
3
类比指数函数的研究过程,借助函数表示获得对数函数的性质,并能进行性质简单应用,从中感受研究函数的方法,进一步积累研究经验.
三、学情分析
教 学 分 析
1.学生已有的认知基础
(1)利用描点法画图,学生已经有了较为丰富的操作经验,能较为熟练地画出一些函数图象.另外,通过对数这一节的学习,学生对于指数与对数的的关系也有了初步的认识,对于必要的对数运算也有了一定程度的训练,这就为探索对数函数图象提供了具体操作经验和一定的运算基础.
(2)通过函数及其性质,指数函数及其性质的学习,学生对于函数研究的内容、过程、方法有了初步的认识;从图象中直观认识函数性质,由特殊到一般的归纳也有了较为丰富的经验,这就为探索对数函数图象和性质提供了直观感知和操作经验.
三、学情分析
教 学 分 析
2.实现目标所需要的认知基础
一方面研究函数的经验相对较少,导致研究线索的梳理并不完备,欠缺设计具体的操作方案的经验;另一方面探索对数函数图象的过程中,缺乏独立寻找共同特征,分类讨论的意识,这些对于如何获得对数函数图象和性质是不利的.
三、教学重点难点
教学难点:具体动手操作,主动探究对数函数图象和性质
突破难点的方法:类比指数函数的研究过程,交流并确认对数函数研究内容和方法,设计具体的操作方案,使学生对探究过程有整体地把握,之后借助自主学习、交流分享,教师及时点评的方式,获得对数函数的图象和性质.
教 学 分 析
四个方面
1.回顾梳理
已有经验
2.通过问题引领学生学习
4.关注学科核心素养的形成和发展
四、教学策略分析
3.学生独立思考,自主操作,交流分享与教师及时点评相结合
教 学 分 析
五、教学过程分析
教 学 过 程
1
2
3
4
5
创设情境、 引入新课
新课讲解
典例讲解
布置作业
课堂小结
一、创设情景,引入新课
(1)指数与对数的关系
a x=N
(a>0,且a≠1)
logaN=x
1.回顾:
(2)指数函数的研究过程,谈谈我们是如何研究的
一、创设情景,引入新课
定义
表示
性质
研究内容:
研究方法:
借助图象和解析式研究函数性质
归纳性质
画具体函数图象
观察图象共同特点
具体操作:
应用
定义域、值域、单调性、奇偶性、定点
1.回顾:
设计意图:通过指数与对数关系的回顾,获得指数
与对数关系的再次巩固;引导学生回顾指数函数的研
究过程,梳理研究具体函数的思路和方法.
2.碳14的衰减规律:
一、创设情景,引入新课
碳14的测代法
一、创设情景,引入新课
训马图 P=0.8267 t=1573
公元433年北魏
斗鸡图 P=0.8385 t=1456
公元550年北周
良渚古玉器
P=0.5267
t=5300
公元前3300年
问题1:“碳14测代法”关系式是否为函数呢?
设计意图:通过指数与对数关系的回顾,获得指数
与对数关系的再次巩固;引导学生回顾指数函数的研
究过程,梳理研究具体函数的思路和方法.
一、创设情景,引入新课
一、创设情景,引入新课
“碳14测代法”函数表达式
问题2:函数表达式形式上有什么特点?
一、创设情景,引入新课
一般形式:
一、创设情景,引入新课
你还能举出一些例子吗?
这类函数的一般形式是什么?
一、创设情景,引入新课
一、创设情景,引入新课
问题3: 函数 表达式中的底数 a的范
围是什么?自变量x的范围呢?
设计意图:组织学生观察思考,认识到对数函数的
一般形式是y=logax ,再借助底数a、自变量x范围的讨
论,经历完整的对数函数概念的抽象过程,为得到对
数函数概念做铺垫.
1.对数函数的定义:
二、新课探究
一般地,函数
其中x是自变量,函数的定义域为.
问题4:类比指数函数的研究过程,我们应该研究对数
函数的哪些内容呢?如何研究呢?
二、新课探究
探究:对数函数图象和性质
2.对数函数图象和性质
定义
表示
性质
研究内容:
研究方法:
借助图象和解析式研究函数性质
归纳性质
画具体函数图象
观察图象共同特点
具体操作:
应用
设计意图:通过类比指数函数的研究过程,获得
对数函数研究的内容、方法、操作方案,体会研究
一个具体函数的研究思路.
活动1 选取底数a的若干个不同值,在同一直角坐标
系内作出相应的对数函数图象。
二、新课探究
2.对数函数图象和性质
探究:对数函数图象和性质
设计意图:学生按照之前的梳理,充分经历动手操
作实践过程,从中积累具体的操作经验.
活动2 观察图象,寻找图象的共同特点、函数的共同性质
二、新课探究
2.对数函数图象和性质
探究:对数函数图象和性质
设计意图:通过经历画具体函数图象,观察函数图
象的共同特点,归纳对数函数图象和性质的活动,获
得研究一类函数图象和性质的具体操作经验,从中感
受研究方法.
图 像
性 质
非奇非偶函数
定义域
值 域
单调性
奇偶性
过定点
x
y
0
1
x
y
0
1
对数函数 的图象和性质
2.对数函数图象和性质
三、典例讲解
例1 求下列函数的定义域:
例2 比较下列各组数中两个值的大小:
设计意图:通过例题,体会对数函数性质的应用
(定义域、单调性),借助单调性比较两个值大小
解决过程,进一步体会运用函数的观点解决问题,
渗透分类讨论的思想.
四、课堂小结
1.本节课研究了对数函数哪些内容?
2.通过本节课的学习,你认为我们是如何研究对数函数?
研究内容:
研究方法:
借助图象和解析式研究函数性质
具体操作:
归纳性质
画具体函数图象
观察图象共同特点
定义
表示
性质
应用
定义域、值域、单调性、定点、奇偶性
设计意图:通过回顾研究过程,进一步加深对研究
方法和具体操作过程的认识,体会研究过程所渗透的
数学思想方法.
五、布置作业
必做题:课本习题2.2 A组7、8
选做题:教材P83习题2.2 B组 2题.
思考题:对数函数 与 的图
象有什么不同吗?你有什么发现?
六、教学反思
高中数学课主要的目的就是培养提出问题和解决问题的能力,而要实现这个目标,就需要在平时的学习中对已有的学习经验进行总结梳理,并注重学生的思维能力以及具体操作的能力提升.因此,本节课设计时,就先设计梳理指数函数的研究过程的环节,之后经历从实际情景中抽象出对数函数的概念,再类比指数函数的研究过程,获得对数函数的研究思路和方法,并设计具体的操作方案后,给予学生充分的时间,独立思考、
六、教学反思
交流分享,教师及时点评,这样设计不仅可以明确对数函数的研究内容和方法,还能在这一过程中发展学生的具体操作能力及数学抽象、数学运算、逻辑推理、直观想象等学科核心素养.从教学的实施情况来看,这样设计的效果很好.另外,在学生观察归纳的过程中,学生没有生成底数互为倒数的两个对数函数的图象关于x轴对称这个结果,因此,我准备在下节课中让学生主动研究这个问题.最后,这节课中有学生回答=0,由于没听清楚,我没有及时纠正,这也提示我在以后的教学中,学生回答问题时,应该集中精神仔细听学生的表达。
2.2.2 对数函数及其性质(1)
高中数学必修1
说 课 程 序
教学内容分析
1
教学目标设置
2
学 情 分 析
3
教学策略分析
4
教学过程分析
5
一、教学内容分析
从函数主题来看
从本节核心来看
从函数主题来看,不仅是对学生已经学习过的函数知识的延伸和拓展,还是后续学习的知识基础,具有承上启下的作用.
教 学 分 析
从本节核心来看,本节课的主要内容始终是围绕着对数函数性质展开的.
教 学 分 析
教学难点:探索对数函数性质
突出重点的方法:类比指数函数的研究过程,交流、共同确认研究对数函数的内容和方法,设计具体的操作方案,并进行具体实践操作,从中体会获得对数函数性质的方法,进一步积累研究经验.
一、教学内容分析
二、教学目标的设置
教 学 分 析
1
通过具体实例,抽象出对数函数概念,了解对数函数概念,发展数学抽象素养.
2
能用描点法画出对数函数图象, 结合具体的对数函数图象,观察共同特点来归纳对数函数的图象,发展数学运算、逻辑推理,直观想象素养.
3
类比指数函数的研究过程,借助函数表示获得对数函数的性质,并能进行性质简单应用,从中感受研究函数的方法,进一步积累研究经验.
三、学情分析
教 学 分 析
1.学生已有的认知基础
(1)利用描点法画图,学生已经有了较为丰富的操作经验,能较为熟练地画出一些函数图象.另外,通过对数这一节的学习,学生对于指数与对数的的关系也有了初步的认识,对于必要的对数运算也有了一定程度的训练,这就为探索对数函数图象提供了具体操作经验和一定的运算基础.
(2)通过函数及其性质,指数函数及其性质的学习,学生对于函数研究的内容、过程、方法有了初步的认识;从图象中直观认识函数性质,由特殊到一般的归纳也有了较为丰富的经验,这就为探索对数函数图象和性质提供了直观感知和操作经验.
三、学情分析
教 学 分 析
2.实现目标所需要的认知基础
一方面研究函数的经验相对较少,导致研究线索的梳理并不完备,欠缺设计具体的操作方案的经验;另一方面探索对数函数图象的过程中,缺乏独立寻找共同特征,分类讨论的意识,这些对于如何获得对数函数图象和性质是不利的.
三、教学重点难点
教学难点:具体动手操作,主动探究对数函数图象和性质
突破难点的方法:类比指数函数的研究过程,交流并确认对数函数研究内容和方法,设计具体的操作方案,使学生对探究过程有整体地把握,之后借助自主学习、交流分享,教师及时点评的方式,获得对数函数的图象和性质.
教 学 分 析
四个方面
1.回顾梳理
已有经验
2.通过问题引领学生学习
4.关注学科核心素养的形成和发展
四、教学策略分析
3.学生独立思考,自主操作,交流分享与教师及时点评相结合
教 学 分 析
五、教学过程分析
教 学 过 程
1
2
3
4
5
创设情境、 引入新课
新课讲解
典例讲解
布置作业
课堂小结
一、创设情景,引入新课
(1)指数与对数的关系
a x=N
(a>0,且a≠1)
logaN=x
1.回顾:
(2)指数函数的研究过程,谈谈我们是如何研究的
一、创设情景,引入新课
定义
表示
性质
研究内容:
研究方法:
借助图象和解析式研究函数性质
归纳性质
画具体函数图象
观察图象共同特点
具体操作:
应用
定义域、值域、单调性、奇偶性、定点
1.回顾:
设计意图:通过指数与对数关系的回顾,获得指数
与对数关系的再次巩固;引导学生回顾指数函数的研
究过程,梳理研究具体函数的思路和方法.
2.碳14的衰减规律:
一、创设情景,引入新课
碳14的测代法
一、创设情景,引入新课
训马图 P=0.8267 t=1573
公元433年北魏
斗鸡图 P=0.8385 t=1456
公元550年北周
良渚古玉器
P=0.5267
t=5300
公元前3300年
问题1:“碳14测代法”关系式是否为函数呢?
设计意图:通过指数与对数关系的回顾,获得指数
与对数关系的再次巩固;引导学生回顾指数函数的研
究过程,梳理研究具体函数的思路和方法.
一、创设情景,引入新课
一、创设情景,引入新课
“碳14测代法”函数表达式
问题2:函数表达式形式上有什么特点?
一、创设情景,引入新课
一般形式:
一、创设情景,引入新课
你还能举出一些例子吗?
这类函数的一般形式是什么?
一、创设情景,引入新课
一、创设情景,引入新课
问题3: 函数 表达式中的底数 a的范
围是什么?自变量x的范围呢?
设计意图:组织学生观察思考,认识到对数函数的
一般形式是y=logax ,再借助底数a、自变量x范围的讨
论,经历完整的对数函数概念的抽象过程,为得到对
数函数概念做铺垫.
1.对数函数的定义:
二、新课探究
一般地,函数
其中x是自变量,函数的定义域为.
问题4:类比指数函数的研究过程,我们应该研究对数
函数的哪些内容呢?如何研究呢?
二、新课探究
探究:对数函数图象和性质
2.对数函数图象和性质
定义
表示
性质
研究内容:
研究方法:
借助图象和解析式研究函数性质
归纳性质
画具体函数图象
观察图象共同特点
具体操作:
应用
设计意图:通过类比指数函数的研究过程,获得
对数函数研究的内容、方法、操作方案,体会研究
一个具体函数的研究思路.
活动1 选取底数a的若干个不同值,在同一直角坐标
系内作出相应的对数函数图象。
二、新课探究
2.对数函数图象和性质
探究:对数函数图象和性质
设计意图:学生按照之前的梳理,充分经历动手操
作实践过程,从中积累具体的操作经验.
活动2 观察图象,寻找图象的共同特点、函数的共同性质
二、新课探究
2.对数函数图象和性质
探究:对数函数图象和性质
设计意图:通过经历画具体函数图象,观察函数图
象的共同特点,归纳对数函数图象和性质的活动,获
得研究一类函数图象和性质的具体操作经验,从中感
受研究方法.
图 像
性 质
非奇非偶函数
定义域
值 域
单调性
奇偶性
过定点
x
y
0
1
x
y
0
1
对数函数 的图象和性质
2.对数函数图象和性质
三、典例讲解
例1 求下列函数的定义域:
例2 比较下列各组数中两个值的大小:
设计意图:通过例题,体会对数函数性质的应用
(定义域、单调性),借助单调性比较两个值大小
解决过程,进一步体会运用函数的观点解决问题,
渗透分类讨论的思想.
四、课堂小结
1.本节课研究了对数函数哪些内容?
2.通过本节课的学习,你认为我们是如何研究对数函数?
研究内容:
研究方法:
借助图象和解析式研究函数性质
具体操作:
归纳性质
画具体函数图象
观察图象共同特点
定义
表示
性质
应用
定义域、值域、单调性、定点、奇偶性
设计意图:通过回顾研究过程,进一步加深对研究
方法和具体操作过程的认识,体会研究过程所渗透的
数学思想方法.
五、布置作业
必做题:课本习题2.2 A组7、8
选做题:教材P83习题2.2 B组 2题.
思考题:对数函数 与 的图
象有什么不同吗?你有什么发现?
六、教学反思
高中数学课主要的目的就是培养提出问题和解决问题的能力,而要实现这个目标,就需要在平时的学习中对已有的学习经验进行总结梳理,并注重学生的思维能力以及具体操作的能力提升.因此,本节课设计时,就先设计梳理指数函数的研究过程的环节,之后经历从实际情景中抽象出对数函数的概念,再类比指数函数的研究过程,获得对数函数的研究思路和方法,并设计具体的操作方案后,给予学生充分的时间,独立思考、
六、教学反思
交流分享,教师及时点评,这样设计不仅可以明确对数函数的研究内容和方法,还能在这一过程中发展学生的具体操作能力及数学抽象、数学运算、逻辑推理、直观想象等学科核心素养.从教学的实施情况来看,这样设计的效果很好.另外,在学生观察归纳的过程中,学生没有生成底数互为倒数的两个对数函数的图象关于x轴对称这个结果,因此,我准备在下节课中让学生主动研究这个问题.最后,这节课中有学生回答=0,由于没听清楚,我没有及时纠正,这也提示我在以后的教学中,学生回答问题时,应该集中精神仔细听学生的表达。
