4.3 对数函数的图象和性质-2021-2022学年高一数学新教材配套教学精品课件(人教A版2019必修第一册)(共23张PPT)
文档属性
| 名称 | 4.3 对数函数的图象和性质-2021-2022学年高一数学新教材配套教学精品课件(人教A版2019必修第一册)(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 697.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
4.3对数函数的图像与性质
1
2
3
对数函数图象的识别
对数函数图象的应用
比较对数值的大小
教学目标
1.掌握对数函数的图象及简单应用.
2.会利用对数函数的单调性比较大小.
核心素养:
1.借助于对数函数的图象的识别与应用,发展直观想象素养.
2.通过对数函数性质的应用,提升数学运算素养.
不等关系与不等式
1.能用不等式(组)表示实际问题的不等关系.
2.初步学会作差法比较两个实数的大小.
核心素养:
通过运用不等式(组)表示实际问题的不等关系及比较两个实数的大小发展数学抽象及数学运算素养.
对数函数y=logax(a>0,且a≠1)的图象和性质
a>1 0图象
对数函数y=logax(a>0,且a≠1)的图象和性质
性 质 定义域 ______________
值域 ____
过定点 过定点________,即x=1时,y=0
函数值 的变化 当01时,________ 当0当x>1时,________
单调性 在(0,+∞)上是________ 在(0,+∞)上是________
(0,+∞)
R
(1,0)
y<0
y>0
y>0
y<0
增函数
减函数
对数函数y=logax(a>0,且a≠1)的图象和性质
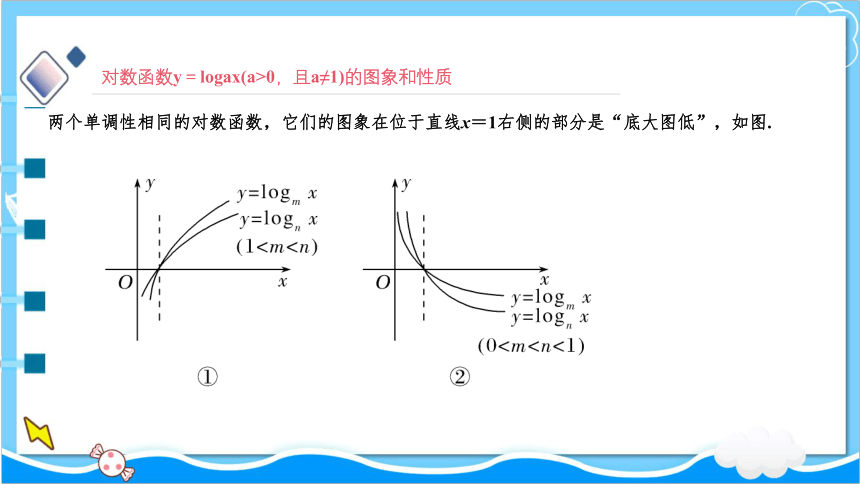
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
[例](多选题)下面列出的不等式中,正确的是( )
解析 a不是负数,可表示成a≥0;
x不大于3可表示成x≤3;
m与4的差是负数,可表示成m-4<0;
x与2的和是非负数,可表示成x+2≥0.
答案:AC
A.a不是负数,可表示成a≥0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m-4<0
D.x与2的和是非负数,可表示成x+2>0
不等关系与不等式
【例】 (1)函数f(x)=1+log2x与g(x)=2-x+1在同一平面直角坐标系中的图象大致是( )
C
对数函数图象的识别
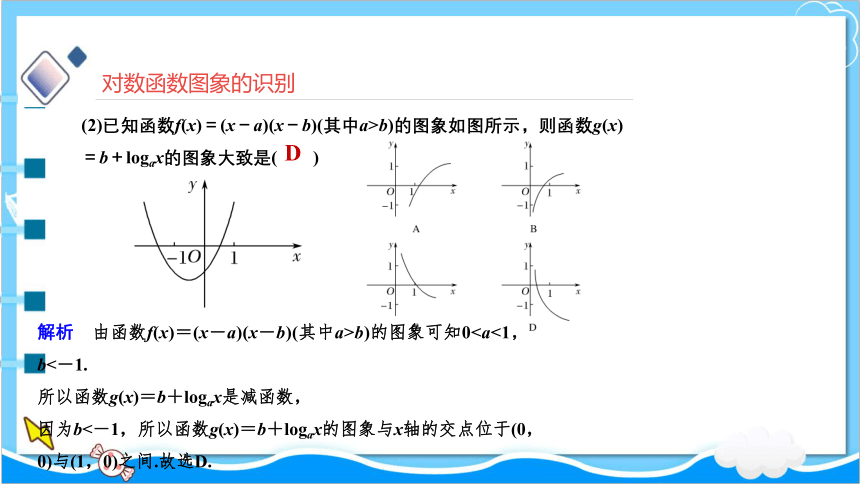
(2)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=b+logax的图象大致是( )
解析 由函数f(x)=(x-a)(x-b)(其中a>b)的图象可知0所以函数g(x)=b+logax是减函数,
因为b<-1,所以函数g(x)=b+logax的图象与x轴的交点位于(0,0)与(1,0)之间.故选D.
对数函数图象的识别
D
有关对数函数图象的识别问题,主要依据底数确定图象是上升还是下降、
图象位置、图象所过定点、图象的平移与翻折变换等求解.
对数函数图象的识别(总结)
【练】 (1)当a>1时,函数y=logax和y=(1-a)x的图象只能是( )
(2)函数y=log2(1-x)的图象是( )
解析 (1)因为a>1,所以y=logax为增函数,且函数图象过定点(1,0),故排除选项C,D.又因为1-a<0,所以直线y=(1-a)x应过原点,且经过第二象限和第四象限.故选B.
(2)易知函数y=log2(1-x)是减函数,故排除A,D,
又函数的定义域为(-∞,1),故可排除B,选C.
对数函数图象的识别
C
B
对数函数图象的应用
B
对数函数图象的应用
对数函数图象的应用
B
在解决求参数的值或取值范围的问题时,利用函数的图象可事半功倍,
作对数函数的图象时,注意底数的变化对其位置的影响.
对数函数图象的应用(总结)
【练】 设a,b是关于x的方程|lg x|=c的两个不同实数根,且a解析 由题意知,在x∈(0,10)上,y=|lg x|的图象和直线y=c有 两个不同交点,作出函数y=|lg x|的图象与直线y=c,如图所示,
结合图象可知,|lg a|=|lg b|=c,
又a∴ab=1,0∴abc的取值范围是(0,1).
对数函数图象的应用
【例】 (1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.b解析 因为函数y=log4x在(0,+∞)上是增函数,a=log23=log49>log46>1,log32<1,所以b比较对数值的大小
D
(2)下列不等式成立的是(其中a>0且a≠1)( )
B
比较对数值的大小
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
比较对数值的大小(总结)
【练】 比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9(2)因为log23>log21=0,log0.32所以log23>log0.32.
比较对数值的大小
1.在对数函数y=logax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0课堂小结
课堂总结
4.3对数函数的图像与性质
1.在对数函数y=logax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0谢谢
欢迎各位专家指导
4.3对数函数的图像与性质
1
2
3
对数函数图象的识别
对数函数图象的应用
比较对数值的大小
教学目标
1.掌握对数函数的图象及简单应用.
2.会利用对数函数的单调性比较大小.
核心素养:
1.借助于对数函数的图象的识别与应用,发展直观想象素养.
2.通过对数函数性质的应用,提升数学运算素养.
不等关系与不等式
1.能用不等式(组)表示实际问题的不等关系.
2.初步学会作差法比较两个实数的大小.
核心素养:
通过运用不等式(组)表示实际问题的不等关系及比较两个实数的大小发展数学抽象及数学运算素养.
对数函数y=logax(a>0,且a≠1)的图象和性质
a>1 0
对数函数y=logax(a>0,且a≠1)的图象和性质
性 质 定义域 ______________
值域 ____
过定点 过定点________,即x=1时,y=0
函数值 的变化 当0
单调性 在(0,+∞)上是________ 在(0,+∞)上是________
(0,+∞)
R
(1,0)
y<0
y>0
y>0
y<0
增函数
减函数
对数函数y=logax(a>0,且a≠1)的图象和性质
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
[例](多选题)下面列出的不等式中,正确的是( )
解析 a不是负数,可表示成a≥0;
x不大于3可表示成x≤3;
m与4的差是负数,可表示成m-4<0;
x与2的和是非负数,可表示成x+2≥0.
答案:AC
A.a不是负数,可表示成a≥0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m-4<0
D.x与2的和是非负数,可表示成x+2>0
不等关系与不等式
【例】 (1)函数f(x)=1+log2x与g(x)=2-x+1在同一平面直角坐标系中的图象大致是( )
C
对数函数图象的识别
(2)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=b+logax的图象大致是( )
解析 由函数f(x)=(x-a)(x-b)(其中a>b)的图象可知0
因为b<-1,所以函数g(x)=b+logax的图象与x轴的交点位于(0,0)与(1,0)之间.故选D.
对数函数图象的识别
D
有关对数函数图象的识别问题,主要依据底数确定图象是上升还是下降、
图象位置、图象所过定点、图象的平移与翻折变换等求解.
对数函数图象的识别(总结)
【练】 (1)当a>1时,函数y=logax和y=(1-a)x的图象只能是( )
(2)函数y=log2(1-x)的图象是( )
解析 (1)因为a>1,所以y=logax为增函数,且函数图象过定点(1,0),故排除选项C,D.又因为1-a<0,所以直线y=(1-a)x应过原点,且经过第二象限和第四象限.故选B.
(2)易知函数y=log2(1-x)是减函数,故排除A,D,
又函数的定义域为(-∞,1),故可排除B,选C.
对数函数图象的识别
C
B
对数函数图象的应用
B
对数函数图象的应用
对数函数图象的应用
B
在解决求参数的值或取值范围的问题时,利用函数的图象可事半功倍,
作对数函数的图象时,注意底数的变化对其位置的影响.
对数函数图象的应用(总结)
【练】 设a,b是关于x的方程|lg x|=c的两个不同实数根,且a
结合图象可知,|lg a|=|lg b|=c,
又a
对数函数图象的应用
【例】 (1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.b
D
(2)下列不等式成立的是(其中a>0且a≠1)( )
B
比较对数值的大小
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
比较对数值的大小(总结)
【练】 比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9
比较对数值的大小
1.在对数函数y=logax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0
课堂总结
4.3对数函数的图像与性质
1.在对数函数y=logax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0
欢迎各位专家指导
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
