5.2.2 平行线的判定 第1课时 课件(共28张ppt)
文档属性
| 名称 | 5.2.2 平行线的判定 第1课时 课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 10:50:58 | ||
图片预览



文档简介
(共28张PPT)
人教版 七年级下
5.2平行线及其判定
精品同步教学课件
5.2.2 平行线的判定(共2课时)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
合作探究
自主学习
随堂练习
拓展提高
课堂小结
5.2平行线及其判定
5.2.2 第1课时 平行线的判定
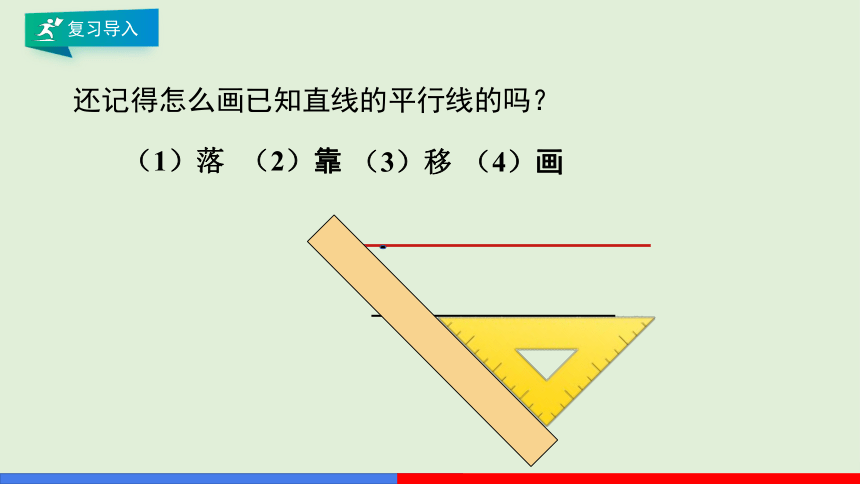
(1)落
(2)靠
(3)移
(4)画
还记得怎么画已知直线的平行线的吗?
复习导入
b
A
2
1
a
B
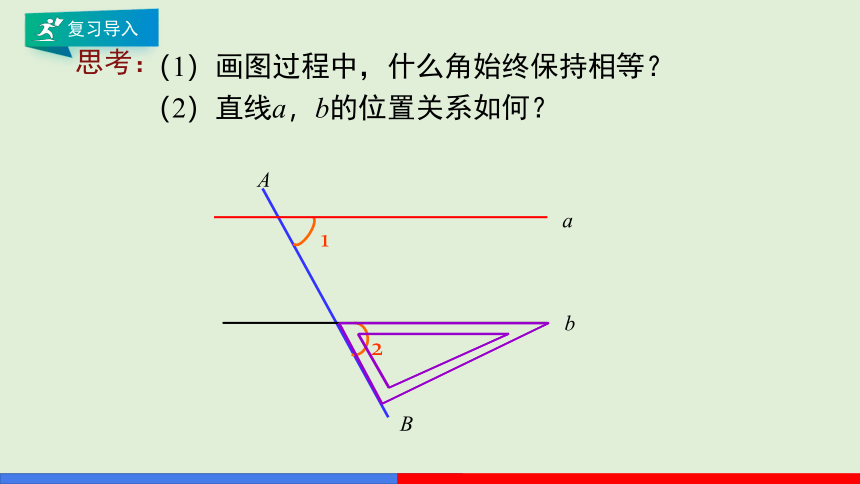
(1)画图过程中,什么角始终保持相等?
(2)直线a,b的位置关系如何?
思考:
复习导入
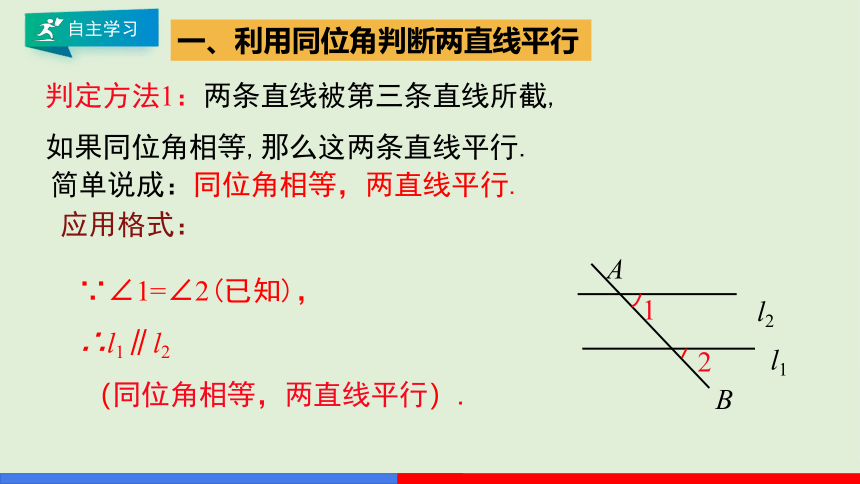
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知),
∴l1∥l2
(同位角相等,两直线平行).
1
2
l2
l1
A
B
一、利用同位角判断两直线平行
自主学习
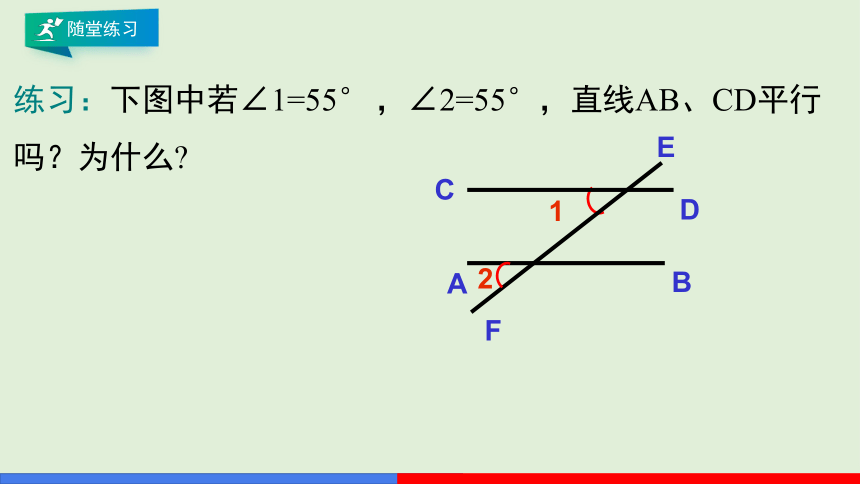
练习:下图中若∠1=55° ,∠2=55°,直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
随堂练习
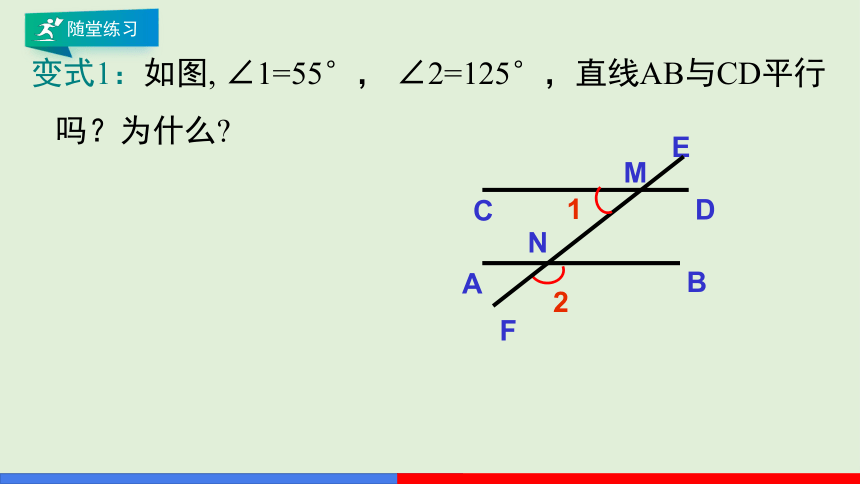
变式1:如图, ∠1=55°, ∠2=125°,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
随堂练习
解: ∵ 3= 2(已知),
1= 3(对顶角相等),
1= 2.
a//b(同位角相等,两直线平行).
2
b
a
1
3
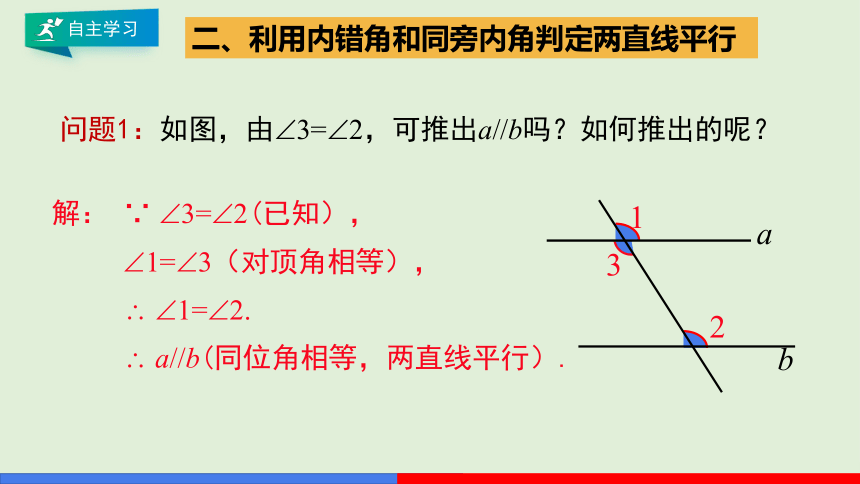
问题1:如图,由 3= 2,可推出a//b吗?如何推出的呢?
二、利用内错角和同旁内角判定两直线平行
自主学习
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
2
b
a
3
自主学习
问题2 如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角的定义)
2= 3(同角的补角相等)
a//b(同位角相等,两直线平行)
2
b
a
1
3
自主学习
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
自主学习
① ∵ ∠2 = ∠ 6(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴___∥___( )
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
例1 根据条件完成填空.
自主学习
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知) ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
课堂小结
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知), ∴_____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
检测: 根据条件完成填空.
课堂检测
5.2平行线及其判定
5.2.2 第2课时 平行线判定方法的综合
到目前为止,判定两直线平行的方法有哪些?
(1)定义法:平面内不相交的两条直线互相平行
(2)平行线公理的推论:平行于同一条直线的两条直线平行.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
复习导入
思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
a
b
c
b⊥a,c⊥a
b∥c
?
猜想:垂直于同一条直线的两条直线平行.
复习导入
如图,在同一平面内,b⊥a,c⊥a,则b∥c.
b
c
1
2
a
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
理由如下:
解:
复习导入
例1如图,已知 ∠1=75o , ∠2 =105o,
AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
解:AB//CD,理由如下:
∵∠1=75°(已知)
∴∠3=180°-∠1=105°(邻补角的定义)
∵∠2=105°(已知)
∴∠2=∠3(等量代换)
∴AB//CD(同位角相等,两直线平行)
典例讲解
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
例2如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行? 为什么?
A
B
D
C
E
F
G
解: (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
典例讲解
例3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
典例讲解
(3)从∠ =∠ 2 ,可以推出AD∥BC,
理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
典例讲解
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
例4.如图,已知∠1= ∠3,AC平分∠DAB,你能判断
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
典例讲解
课本练习第1题和课后习题第4题
随堂练行线的判定6种方法:
1.定义法:同一平面内,不相交的两条直线平行.
2.平行线的基本事实的推论:平行于同一条直线的两条直线平行
3.同位角相等,两直线平行;
4.内错角相等,两直线平行;
5.同旁内角互补,两直线平行.
6.同一平面内,垂直于同一直线的两直线平行.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
5.2平行线及其判定
精品同步教学课件
5.2.2 平行线的判定(共2课时)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础一般的学生使用。课件包括以下环节:
新知引入
合作探究
自主学习
随堂练习
拓展提高
课堂小结
5.2平行线及其判定
5.2.2 第1课时 平行线的判定
(1)落
(2)靠
(3)移
(4)画
还记得怎么画已知直线的平行线的吗?
复习导入
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b的位置关系如何?
思考:
复习导入
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知),
∴l1∥l2
(同位角相等,两直线平行).
1
2
l2
l1
A
B
一、利用同位角判断两直线平行
自主学习
练习:下图中若∠1=55° ,∠2=55°,直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
随堂练习
变式1:如图, ∠1=55°, ∠2=125°,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
随堂练习
解: ∵ 3= 2(已知),
1= 3(对顶角相等),
1= 2.
a//b(同位角相等,两直线平行).
2
b
a
1
3
问题1:如图,由 3= 2,可推出a//b吗?如何推出的呢?
二、利用内错角和同旁内角判定两直线平行
自主学习
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
2
b
a
3
自主学习
问题2 如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角的定义)
2= 3(同角的补角相等)
a//b(同位角相等,两直线平行)
2
b
a
1
3
自主学习
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
自主学习
① ∵ ∠2 = ∠ 6(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴___∥___( )
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
例1 根据条件完成填空.
自主学习
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知) ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
课堂小结
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知), ∴_____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
检测: 根据条件完成填空.
课堂检测
5.2平行线及其判定
5.2.2 第2课时 平行线判定方法的综合
到目前为止,判定两直线平行的方法有哪些?
(1)定义法:平面内不相交的两条直线互相平行
(2)平行线公理的推论:平行于同一条直线的两条直线平行.
(3)判定方法1:同位角相等,两直线平行.
(4)判定方法2:内错角相等,两直线平行.
(5)判定方法3:同旁内角互补,两直线平行.
复习导入
思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
a
b
c
b⊥a,c⊥a
b∥c
?
猜想:垂直于同一条直线的两条直线平行.
复习导入
如图,在同一平面内,b⊥a,c⊥a,则b∥c.
b
c
1
2
a
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
理由如下:
解:
复习导入
例1如图,已知 ∠1=75o , ∠2 =105o,
AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75o
105o
还有其它解法吗?
解:AB//CD,理由如下:
∵∠1=75°(已知)
∴∠3=180°-∠1=105°(邻补角的定义)
∵∠2=105°(已知)
∴∠2=∠3(等量代换)
∴AB//CD(同位角相等,两直线平行)
典例讲解
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
例2如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行? 为什么?
A
B
D
C
E
F
G
解: (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
典例讲解
例3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
典例讲解
(3)从∠ =∠ 2 ,可以推出AD∥BC,
理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
典例讲解
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
例4.如图,已知∠1= ∠3,AC平分∠DAB,你能判断
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
典例讲解
课本练习第1题和课后习题第4题
随堂练行线的判定6种方法:
1.定义法:同一平面内,不相交的两条直线平行.
2.平行线的基本事实的推论:平行于同一条直线的两条直线平行
3.同位角相等,两直线平行;
4.内错角相等,两直线平行;
5.同旁内角互补,两直线平行.
6.同一平面内,垂直于同一直线的两直线平行.
课堂小结
https://www.21cnjy.com/help/help_extract.php
