2021-2022学年高一下学期数学北师大版(2019)必修第二册2.1位移、速度、力与向量的概念 课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册2.1位移、速度、力与向量的概念 课件(共34张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
§ 2.1 位移、速度、力与向量的概念
北师大(2019)必修2
聚焦知识目标和数学素养
(1)在向量概念形成过程中,理解向量概念,培养学生的数学抽象、逻辑推理、数学运算素养;
(2)在概念教学的具体应用中,培养学生的数学建模、直观想象素养
环节一
情境引入
情境引入
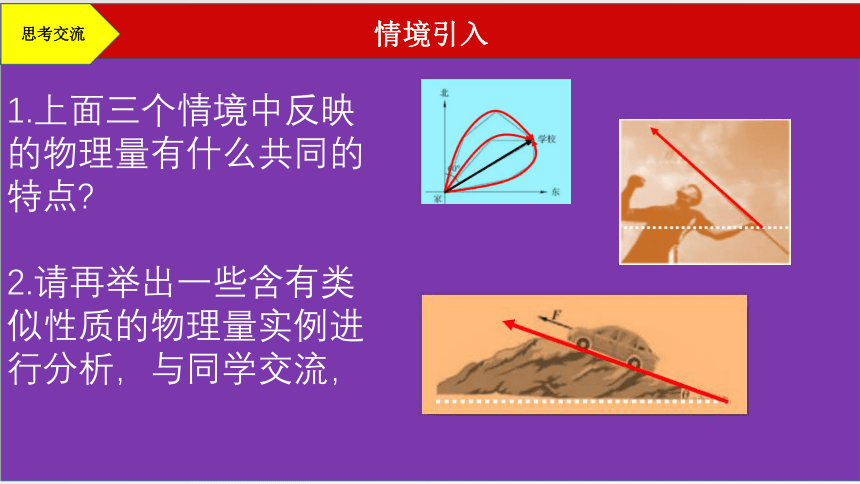
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
学校位于小明家北偏东60°方向,距离小明家2000m.从小明家到学校,可能有长短不同的几条路.无论走哪条路,位移都是向北偏东60°方向移动了2000m
情境1
情境引入
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
某著名运动员投掷标枪时,其中一次记录为:出手角度θ=43.242°,出手速率为v=28.35m/s
情境2
情境引入
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
汽车沿倾斜角为θ的坡路向上行驶,汽车的牵引力为F.
情境3
情境引入
1.上面三个情境中反映的物理量有什么共同的特点
2.请再举出一些含有类似性质的物理量实例进行分析,与同学交流,
思考交流
环节二
向量的概念与表示
向量的概念与表示
基于上述讨论,我们发现,位移、速度和力这些物理量都是既有大小又有方向的量,它们等和长度、面积、质量等只有大小的量不同.在现实世界中,像位移、速度、力等既有大小又有方向向的量还有很多,如加速度、动量等.
既有大小又有方向的量统称为向量.
那些只有大小没有方向的量称为数量(如年龄、长度、体重、面积、体积等)
向量概念
向量的概念与表示
在物理学中,位移、速度和力通常用一条带箭头的线段表示,箭头表示这些量的方向,线段长度表示这些量的大小.
在数学中,这种具有方向和长度的线段称为有向线段(如图).以A为起点,B为终点的有向线段,记作.线段AB的长度称为有向线段的长度,记作I|
有向线段
A(起点)
B(终点)
向量的概念与表示
向量可以用有向线段表示,其中有向线段的长度表示向量的大小,箭头所指的方向表示(向量的方向.向量也可以用黑斜体小写字母如a,b.c.…或.,,…(书写)来表示.向量的大小,记作||,又称作向量的模.
向量表示
向量的概念与表示
有向线段就是向量,对吗
思考
不对.有向线段的起点、终点是确定的,而向量与起点无关,可以自由平移,它可以用有向线段表示,但不能说有向线段就是向量.
向量的概念与表示
长度为0的向量称为零向量,记作0或,任何方向都可以作为零向量的方向.
零向量
向量的概念与表示
模等于1个单位长度的向量称为单位向量.
单位向量
向量的概念与表示
例1.小明从学校的教学楼出发,向北走了1500m到达图书馆,2h后又从图书馆向南偏东60°走了1000m到食堂就餐,用餐后又从食堂向西走2000m来到操场运动,请选择适当的比例尺画图,用向量表示小明每次的位移
北
东
A(图书馆)
B(食堂)
C(操场)
O(教学楼)
解:设比例尺为1:50000,小明的位移向量表示从教学楼到图书馆的距离与方向;向量表示从图书馆到食堂的距离与方向;向量 表示从食堂到操场的距离与方向.
向量的概念与表示
1.画图表示小船的下列位移(用1:500000的比例尺);
(1)由A地向东北方向航行15km到达B地;
(2)由A地向北偏西30°方向航行20km到达C地;
(3)由C地向正南方向航行25km到达D地.
北
东
向量的概念与表示
2. 在平面直角坐标系xOy中有三点A(1,0),B(-1,2),C(-2,2),请用有向线段分别表示由A到B,由B到C,由C到A的位移.
A(1,0)
B(-1,2)
C(-2,2)
环节三
向量的基本关系
向量的基本关系
在物理学中,两个物体运动速度相等是指它们的方向相同、大小相等;两个力相等不仅包括方向相同、大小相等,还包括作用点相同.
相等向量
在数学中,相等向量是指它们的长度相等且方向相同.向量与相等,记作=,若两条有向线段方向相同、长度相等,则它们表示的向量是相等
向量的基本关系
相等向量
代表相等向量的有向线段与起点位置无关.直观地说,一条有向线 段在平移过程中,虽然位置不同,但表示的是相等向量
向量的基本关系
共线(平行)向量
若两个非零向量.的方向相同或相反,则称这两个向量为共线向量或平行向量,也称这两个向量共线或平行,记作/.
长度不限,可以同向
(所在直线可以平行,可以重合)
长度不限,可以反向(所在直线可以平行,可以重合)
规定零向量与任一向量共线,即对于任意的向量,都有/.
向量的基本关系
相反向量
若两个向量的长度相等,方向相反,则称它们互为相反向量.相反向量是共线向量.若其中一个向量为,则它的相反向量记作-.
(所在直线可以平行,可以重合)
零向量的相反向量仍是零向量.
向量基本关系小结
零向量 长度为0的向量称为零向量,记作0.任何方向都可以作为零向量的方向.
单位向量 模等于1个单位长度的向量称为单位向量.
相等向量 长度相等且方向相同的向量,叫作相等向量.向量a与b相等,记作a=b.
共线(平行) 向量 若两个非零向量的方向相同或相反,则称这两个向量为共线向量或平行向量.a与b共线或平行,记作a∥b.零向量与任一向量共线.
相反向量 若两个向量的长度相等、方向相反,则称它们互为相反向量. 向量a的相反向量记作-a.
向量基本关系
例2.如图,△ABC和△A′B′C′是在各边的 处相交的两个全等的等边三角形,设△ABC的边长为a,图中列出了长度均为 的若干个向量,则
(1)与向量 相等的向量有________;
(2)与向量 共线,且模相等的向量有________;
(3)与向量 共线,且模相等的向量有________.
环节四
向量的夹角
向量的夹角
(1)定义:已知两个非零向量a和b,在平面内选一点O,作 =, =,
则θ=∠AOB称为向量a与b的夹角;
(2)范围:0°≤θ≤180°;
(3)大小与向量共线、垂直的关系:
O
向量的夹角
例3如图,等边三角形ABC中,点D,E,F分别是边B,BC,AC的中点,指出如下各组向量的夹角.
(1)与
(2)与
环节五
学习与反思
1.用有向线段表示两个相等的向量,这两个有向线段一定重合吗
2.判断下列结论是否正确(正确的在括号内画“√”,错误的画“×”),并说明理由.
(1)长度相等的两个向量一定是相等向量.()
(2)相等向量的起点必定相同.()
(3)向量AB的长度与向量BA的长度相等.()
(4)物理学中的作用力和反作用力是一对共线向量.()
2.判断下列结论是否正确(正确的在括号内画“√”,错误的画“×”),并说明理由.
(1)长度相等的两个向量一定是相等向量.()
(2)相等向量的起点必定相同.()
(3)向量的长度与向量的长度相等.()
(4)物理学中的作用力和反作用力是一对共线向量.()
(5)若与都是单位向量,则=.()
3.在矩形ABCD中,AB=2BC,点M,N分别为AB和CD的中点.在以点A、B,C,D,M,N为起点或终点的向量中,相等的非零向量共有多少对?
4、在等边三角形ABC中,与的夹角为 ,点E为BC的中点,则与的夹角为_.
§ 2.1 位移、速度、力与向量的概念
北师大(2019)必修2
聚焦知识目标和数学素养
(1)在向量概念形成过程中,理解向量概念,培养学生的数学抽象、逻辑推理、数学运算素养;
(2)在概念教学的具体应用中,培养学生的数学建模、直观想象素养
环节一
情境引入
情境引入
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
学校位于小明家北偏东60°方向,距离小明家2000m.从小明家到学校,可能有长短不同的几条路.无论走哪条路,位移都是向北偏东60°方向移动了2000m
情境1
情境引入
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
某著名运动员投掷标枪时,其中一次记录为:出手角度θ=43.242°,出手速率为v=28.35m/s
情境2
情境引入
在物理学中,我们学习过"位移”“速度”和“力”等物理量.下面各情境分别反映了这些物理量.
汽车沿倾斜角为θ的坡路向上行驶,汽车的牵引力为F.
情境3
情境引入
1.上面三个情境中反映的物理量有什么共同的特点
2.请再举出一些含有类似性质的物理量实例进行分析,与同学交流,
思考交流
环节二
向量的概念与表示
向量的概念与表示
基于上述讨论,我们发现,位移、速度和力这些物理量都是既有大小又有方向的量,它们等和长度、面积、质量等只有大小的量不同.在现实世界中,像位移、速度、力等既有大小又有方向向的量还有很多,如加速度、动量等.
既有大小又有方向的量统称为向量.
那些只有大小没有方向的量称为数量(如年龄、长度、体重、面积、体积等)
向量概念
向量的概念与表示
在物理学中,位移、速度和力通常用一条带箭头的线段表示,箭头表示这些量的方向,线段长度表示这些量的大小.
在数学中,这种具有方向和长度的线段称为有向线段(如图).以A为起点,B为终点的有向线段,记作.线段AB的长度称为有向线段的长度,记作I|
有向线段
A(起点)
B(终点)
向量的概念与表示
向量可以用有向线段表示,其中有向线段的长度表示向量的大小,箭头所指的方向表示(向量的方向.向量也可以用黑斜体小写字母如a,b.c.…或.,,…(书写)来表示.向量的大小,记作||,又称作向量的模.
向量表示
向量的概念与表示
有向线段就是向量,对吗
思考
不对.有向线段的起点、终点是确定的,而向量与起点无关,可以自由平移,它可以用有向线段表示,但不能说有向线段就是向量.
向量的概念与表示
长度为0的向量称为零向量,记作0或,任何方向都可以作为零向量的方向.
零向量
向量的概念与表示
模等于1个单位长度的向量称为单位向量.
单位向量
向量的概念与表示
例1.小明从学校的教学楼出发,向北走了1500m到达图书馆,2h后又从图书馆向南偏东60°走了1000m到食堂就餐,用餐后又从食堂向西走2000m来到操场运动,请选择适当的比例尺画图,用向量表示小明每次的位移
北
东
A(图书馆)
B(食堂)
C(操场)
O(教学楼)
解:设比例尺为1:50000,小明的位移向量表示从教学楼到图书馆的距离与方向;向量表示从图书馆到食堂的距离与方向;向量 表示从食堂到操场的距离与方向.
向量的概念与表示
1.画图表示小船的下列位移(用1:500000的比例尺);
(1)由A地向东北方向航行15km到达B地;
(2)由A地向北偏西30°方向航行20km到达C地;
(3)由C地向正南方向航行25km到达D地.
北
东
向量的概念与表示
2. 在平面直角坐标系xOy中有三点A(1,0),B(-1,2),C(-2,2),请用有向线段分别表示由A到B,由B到C,由C到A的位移.
A(1,0)
B(-1,2)
C(-2,2)
环节三
向量的基本关系
向量的基本关系
在物理学中,两个物体运动速度相等是指它们的方向相同、大小相等;两个力相等不仅包括方向相同、大小相等,还包括作用点相同.
相等向量
在数学中,相等向量是指它们的长度相等且方向相同.向量与相等,记作=,若两条有向线段方向相同、长度相等,则它们表示的向量是相等
向量的基本关系
相等向量
代表相等向量的有向线段与起点位置无关.直观地说,一条有向线 段在平移过程中,虽然位置不同,但表示的是相等向量
向量的基本关系
共线(平行)向量
若两个非零向量.的方向相同或相反,则称这两个向量为共线向量或平行向量,也称这两个向量共线或平行,记作/.
长度不限,可以同向
(所在直线可以平行,可以重合)
长度不限,可以反向(所在直线可以平行,可以重合)
规定零向量与任一向量共线,即对于任意的向量,都有/.
向量的基本关系
相反向量
若两个向量的长度相等,方向相反,则称它们互为相反向量.相反向量是共线向量.若其中一个向量为,则它的相反向量记作-.
(所在直线可以平行,可以重合)
零向量的相反向量仍是零向量.
向量基本关系小结
零向量 长度为0的向量称为零向量,记作0.任何方向都可以作为零向量的方向.
单位向量 模等于1个单位长度的向量称为单位向量.
相等向量 长度相等且方向相同的向量,叫作相等向量.向量a与b相等,记作a=b.
共线(平行) 向量 若两个非零向量的方向相同或相反,则称这两个向量为共线向量或平行向量.a与b共线或平行,记作a∥b.零向量与任一向量共线.
相反向量 若两个向量的长度相等、方向相反,则称它们互为相反向量. 向量a的相反向量记作-a.
向量基本关系
例2.如图,△ABC和△A′B′C′是在各边的 处相交的两个全等的等边三角形,设△ABC的边长为a,图中列出了长度均为 的若干个向量,则
(1)与向量 相等的向量有________;
(2)与向量 共线,且模相等的向量有________;
(3)与向量 共线,且模相等的向量有________.
环节四
向量的夹角
向量的夹角
(1)定义:已知两个非零向量a和b,在平面内选一点O,作 =, =,
则θ=∠AOB称为向量a与b的夹角;
(2)范围:0°≤θ≤180°;
(3)大小与向量共线、垂直的关系:
O
向量的夹角
例3如图,等边三角形ABC中,点D,E,F分别是边B,BC,AC的中点,指出如下各组向量的夹角.
(1)与
(2)与
环节五
学习与反思
1.用有向线段表示两个相等的向量,这两个有向线段一定重合吗
2.判断下列结论是否正确(正确的在括号内画“√”,错误的画“×”),并说明理由.
(1)长度相等的两个向量一定是相等向量.()
(2)相等向量的起点必定相同.()
(3)向量AB的长度与向量BA的长度相等.()
(4)物理学中的作用力和反作用力是一对共线向量.()
2.判断下列结论是否正确(正确的在括号内画“√”,错误的画“×”),并说明理由.
(1)长度相等的两个向量一定是相等向量.()
(2)相等向量的起点必定相同.()
(3)向量的长度与向量的长度相等.()
(4)物理学中的作用力和反作用力是一对共线向量.()
(5)若与都是单位向量,则=.()
3.在矩形ABCD中,AB=2BC,点M,N分别为AB和CD的中点.在以点A、B,C,D,M,N为起点或终点的向量中,相等的非零向量共有多少对?
4、在等边三角形ABC中,与的夹角为 ,点E为BC的中点,则与的夹角为_.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
