人教版数学八年级上册13.3.1等腰三角形(2)课件(17张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形(2)课件(17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 21:04:51 | ||
图片预览




文档简介
(共17张PPT)
第十三章 轴对称
13.3.1 等腰三角形(2)
生
活
中
的
数
学
生
活
中
的
数
学
类比探究
猜想:如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
等腰三角形
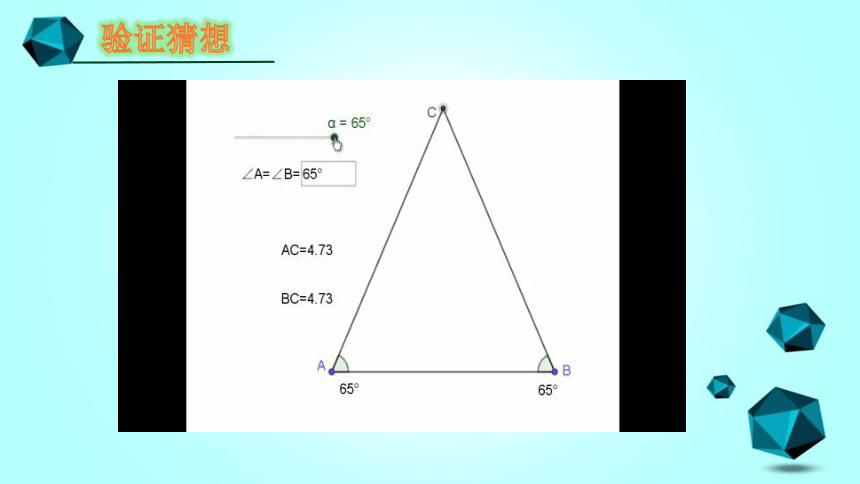
验证猜想
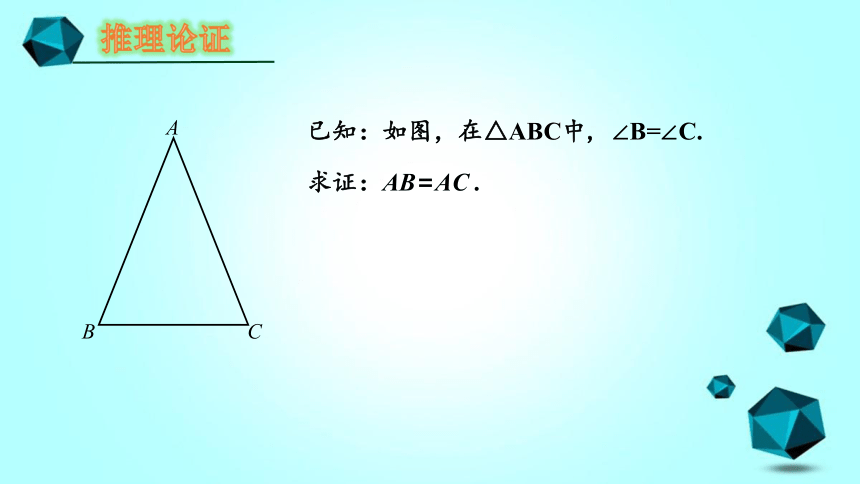
推理论证
A
B
C
已知:如图,在△ABC中, ∠B=∠C.
求证:AB=AC .
归纳方法
∴ AC =AB (等角对等边).
即△ABC为等腰三角形.
∵∠B =∠C (已知),
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法
在△ABC中,
归纳方法
A
B
C
A
B
C
判定方法1:定义法
AB=AC
判定方法2:等角对等边
∠B=∠C
典例解析
例1 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC ,
∴∠1=∠B (两直线平行,同位角相等),
∠2 =∠C (两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B =∠C ,
∴AB =AC (等角对等边).
A
B
C
E
(
(
1
2
D
变式训练
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
F
典例解析
例2 如图,AC 和 BD 相交于点O,且AB//DC,OA =OB.
求证:OC =OD.
D
O
C
B
A
(A套餐)
1.如图,∠A=36°,∠DBC=36°,
∠C=72°,请说出图中有哪些等腰
三角形.
2.如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
(B套餐)
1.如图,∠BAC=108°,∠B=36°,∠ADB=72°,请说出图中有哪些等腰三角形.
2.如图,∠A=∠B,CE∥DA,CE交AB于E.求证:△CEB是等腰三角形.
独立完成
交换批阅
讲给同伴
A
C
D
B
A
B
C
D
B
A
C
D
E
课堂小结
问1:通过这节课的学习,你收获了几种等腰三角形
的判定方法?
问2:如何区分等腰三角形的性质和判定?
课堂小结
性质:等边对等角
判定:等角对等边
互为逆定理
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
应用格式:
∵ ∠B=∠C,
∴ AB=AC(等角对等边).
问1:通过这节课的学习,你收获了几种等腰三角形
的判定方法?
问3:证明线段相等的方法有哪些?
问2:如何区分等腰三角形的性质和判定?
课堂小结
课后 作业
1.(巩固类作业)课本92页第6题;
2.(提升类作业)课本83页第10题;
3.(应用类作业)课本83页第11题.
同学们再见!
第十三章 轴对称
13.3.1 等腰三角形(2)
生
活
中
的
数
学
生
活
中
的
数
学
类比探究
猜想:如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
等腰三角形
验证猜想
推理论证
A
B
C
已知:如图,在△ABC中, ∠B=∠C.
求证:AB=AC .
归纳方法
∴ AC =AB (等角对等边).
即△ABC为等腰三角形.
∵∠B =∠C (已知),
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法
在△ABC中,
归纳方法
A
B
C
A
B
C
判定方法1:定义法
AB=AC
判定方法2:等角对等边
∠B=∠C
典例解析
例1 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC ,
∴∠1=∠B (两直线平行,同位角相等),
∠2 =∠C (两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B =∠C ,
∴AB =AC (等角对等边).
A
B
C
E
(
(
1
2
D
变式训练
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
F
典例解析
例2 如图,AC 和 BD 相交于点O,且AB//DC,OA =OB.
求证:OC =OD.
D
O
C
B
A
(A套餐)
1.如图,∠A=36°,∠DBC=36°,
∠C=72°,请说出图中有哪些等腰
三角形.
2.如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
(B套餐)
1.如图,∠BAC=108°,∠B=36°,∠ADB=72°,请说出图中有哪些等腰三角形.
2.如图,∠A=∠B,CE∥DA,CE交AB于E.求证:△CEB是等腰三角形.
独立完成
交换批阅
讲给同伴
A
C
D
B
A
B
C
D
B
A
C
D
E
课堂小结
问1:通过这节课的学习,你收获了几种等腰三角形
的判定方法?
问2:如何区分等腰三角形的性质和判定?
课堂小结
性质:等边对等角
判定:等角对等边
互为逆定理
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
应用格式:
∵ ∠B=∠C,
∴ AB=AC(等角对等边).
问1:通过这节课的学习,你收获了几种等腰三角形
的判定方法?
问3:证明线段相等的方法有哪些?
问2:如何区分等腰三角形的性质和判定?
课堂小结
课后 作业
1.(巩固类作业)课本92页第6题;
2.(提升类作业)课本83页第10题;
3.(应用类作业)课本83页第11题.
同学们再见!
