2021--2022学年人教版九年级数学下册27.3位似教学(共18张ppt)
文档属性
| 名称 | 2021--2022学年人教版九年级数学下册27.3位似教学(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 07:58:14 | ||
图片预览


文档简介
(共18张PPT)
人教版九年级下册
§27.3 位 似
一、文化熏陶 感受位似
形状、大小没有改变,位置发生变化
一、文化熏陶 感受位似
“景到,在午有端,与景长。说在端。”
-----《墨经》
形状没有改变,大小、位置发生变化
平移
C
'
B
'
定义
性质
画图
坐标表示
应用
A
A
'
C
C
'
B
B
'
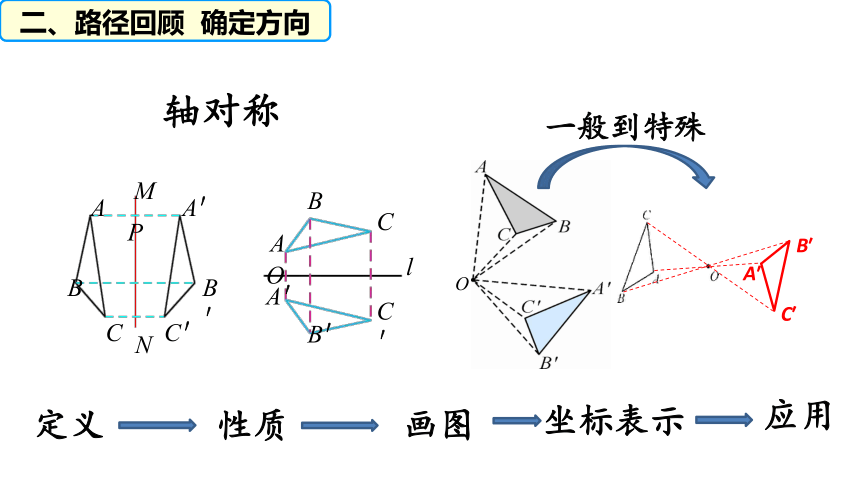
二、路径回顾 确定方向
轴对称
定义
A
B
C
M
N
P
A′
B′
C′
性质
A
B
C
l
O
A′
B′
C′
画图
坐标表示
应用
O
A′
B′
C′
二、路径回顾 确定方向
一般到特殊
A′
B′
C′
A
A
'
C
C
'
B
B
'
A
B
C
M
N
P
A′
B′
C′
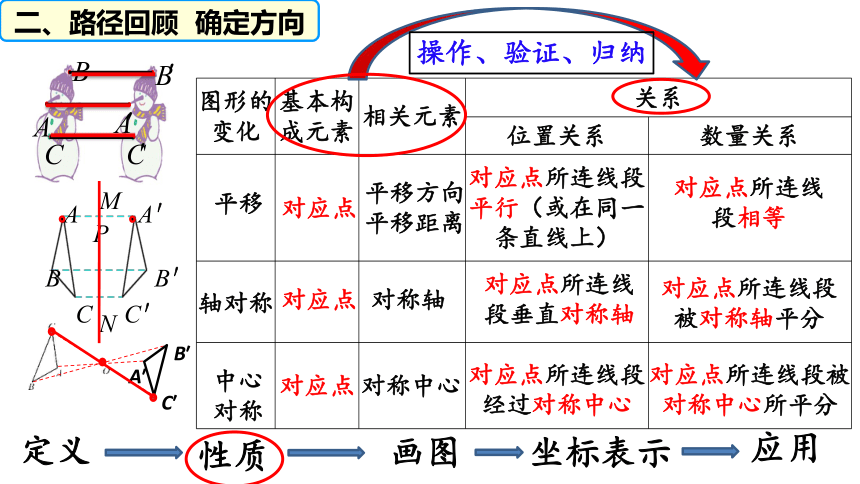
图形的变化 基本构成元素 相关元素 关系
位置关系 数量关系
定义
性质
画图
坐标表示
应用
二、路径回顾 确定方向
对应点所连线段平行(或在同一条直线上)
平移
对应点所连线段相等
轴对称
对应点所连线段垂直对称轴
对应点所连线段被对称轴平分
对应点所连线段被对称中心所平分
对应点所连线段经过对称中心
中心
对称
对应点
对应点
对应点
平移方向
平移距离
对称轴
对称中心
操作、验证、归纳
三、类比方法 初探位似
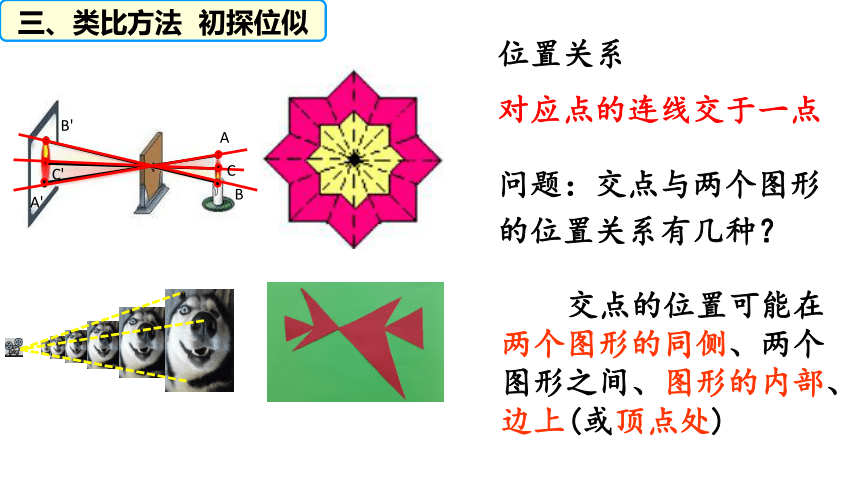
对应点的连线交于一点
位置关系
问题:交点与两个图形的位置关系有几种?
交点的位置可能在两个图形的同侧、两个图形之间、图形的内部、边上(或顶点处)
A
A'
B
B'
C
C'
请将两个相似的直角三角形摆成具有特殊位置关系(每组对应点的连线交于一点)的图形,请尝试,并说明你的摆放方法。
三、类比方法 再探位似
活动一
问题:类比平移、旋转、轴对称性质的研究,要探 究这种图形变化下的数量关系,你觉得应该从哪方面进行研究?用什么方法进行研究?
三、类比方法 再探位似
活动二
2.并计算它们的比值,你有什么发现?
操作发现:
1.度量对应点到交点的距离
三、类比方法 归纳位似
归纳:
如果一个图形上的点A,B,…,D,…和另一个图形上的点A',B',…,D',…分别对应,并且它们的连线AA',BB',…,DD',…都经过同一个点O, ,那么这两个图形叫做位似图形,点O是位似中心。
请你以点O为位似中心,把△ABC放大为原来的2倍.
四、应用概念 试画位似
A
C
B
O
活动三:
画位似图形的一般步骤:
①分别连接并延长位似中心和能代表原图的关键点;
②根据相似比,确定能代表所作的位似图形的关键点;
③顺次连接上述各点,得到所做的位似图形.
四、应用概念 试画位似
活动四:
作用:
利用位似,可以将一个图形放大或缩小
你能把△ABC缩小到原来的 吗?请尝试.
A
C
B
1.如所示的图案中,你能找到哪些图形的变化呢
五、巩固应用 强化位似
2.在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏。如图,点P为放映机的光源,△ABC是胶片上的画面,△A'B'C'为银幕上看到的画面。若胶片上图片的规格是2.5cm×2.5cm,放映的银幕规格是2m×2m,光源P与胶片的距离是20cm,则银幕应距离光源P多远时,放映的图象正好布满整个银幕?
五、巩固应用 强化位似
P
A
B
C
A'
C'
B'
怎样学
学什么
为什么这样学
六、归纳梳理 总结提升
观察(共同结构特征)
平移、轴对称、旋转
位似
类比
操作、验证
归纳(由特殊到一般)
数学知识之间是互相联系的
具有共同特征的一类数学对象具有类似的研究路径
畅所欲言 谈收获
1.梳理作业:
2.实践作业:
利用图形的变化(平移、轴对称、旋转、位似)设计一幅作品.(组内评比后,在全班进行交流、展示.)
七、布置作业 巩固新知
图形的变化 基本构成元素 相关元素 关系
位置关系 数量关系
平移
轴对称
中心对称
位似
美丽图片 赏位似
18
谢谢聆听 欢迎指导!
人教版九年级下册
§27.3 位 似
一、文化熏陶 感受位似
形状、大小没有改变,位置发生变化
一、文化熏陶 感受位似
“景到,在午有端,与景长。说在端。”
-----《墨经》
形状没有改变,大小、位置发生变化
平移
C
'
B
'
定义
性质
画图
坐标表示
应用
A
A
'
C
C
'
B
B
'
二、路径回顾 确定方向
轴对称
定义
A
B
C
M
N
P
A′
B′
C′
性质
A
B
C
l
O
A′
B′
C′
画图
坐标表示
应用
O
A′
B′
C′
二、路径回顾 确定方向
一般到特殊
A′
B′
C′
A
A
'
C
C
'
B
B
'
A
B
C
M
N
P
A′
B′
C′
图形的变化 基本构成元素 相关元素 关系
位置关系 数量关系
定义
性质
画图
坐标表示
应用
二、路径回顾 确定方向
对应点所连线段平行(或在同一条直线上)
平移
对应点所连线段相等
轴对称
对应点所连线段垂直对称轴
对应点所连线段被对称轴平分
对应点所连线段被对称中心所平分
对应点所连线段经过对称中心
中心
对称
对应点
对应点
对应点
平移方向
平移距离
对称轴
对称中心
操作、验证、归纳
三、类比方法 初探位似
对应点的连线交于一点
位置关系
问题:交点与两个图形的位置关系有几种?
交点的位置可能在两个图形的同侧、两个图形之间、图形的内部、边上(或顶点处)
A
A'
B
B'
C
C'
请将两个相似的直角三角形摆成具有特殊位置关系(每组对应点的连线交于一点)的图形,请尝试,并说明你的摆放方法。
三、类比方法 再探位似
活动一
问题:类比平移、旋转、轴对称性质的研究,要探 究这种图形变化下的数量关系,你觉得应该从哪方面进行研究?用什么方法进行研究?
三、类比方法 再探位似
活动二
2.并计算它们的比值,你有什么发现?
操作发现:
1.度量对应点到交点的距离
三、类比方法 归纳位似
归纳:
如果一个图形上的点A,B,…,D,…和另一个图形上的点A',B',…,D',…分别对应,并且它们的连线AA',BB',…,DD',…都经过同一个点O, ,那么这两个图形叫做位似图形,点O是位似中心。
请你以点O为位似中心,把△ABC放大为原来的2倍.
四、应用概念 试画位似
A
C
B
O
活动三:
画位似图形的一般步骤:
①分别连接并延长位似中心和能代表原图的关键点;
②根据相似比,确定能代表所作的位似图形的关键点;
③顺次连接上述各点,得到所做的位似图形.
四、应用概念 试画位似
活动四:
作用:
利用位似,可以将一个图形放大或缩小
你能把△ABC缩小到原来的 吗?请尝试.
A
C
B
1.如所示的图案中,你能找到哪些图形的变化呢
五、巩固应用 强化位似
2.在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏。如图,点P为放映机的光源,△ABC是胶片上的画面,△A'B'C'为银幕上看到的画面。若胶片上图片的规格是2.5cm×2.5cm,放映的银幕规格是2m×2m,光源P与胶片的距离是20cm,则银幕应距离光源P多远时,放映的图象正好布满整个银幕?
五、巩固应用 强化位似
P
A
B
C
A'
C'
B'
怎样学
学什么
为什么这样学
六、归纳梳理 总结提升
观察(共同结构特征)
平移、轴对称、旋转
位似
类比
操作、验证
归纳(由特殊到一般)
数学知识之间是互相联系的
具有共同特征的一类数学对象具有类似的研究路径
畅所欲言 谈收获
1.梳理作业:
2.实践作业:
利用图形的变化(平移、轴对称、旋转、位似)设计一幅作品.(组内评比后,在全班进行交流、展示.)
七、布置作业 巩固新知
图形的变化 基本构成元素 相关元素 关系
位置关系 数量关系
平移
轴对称
中心对称
位似
美丽图片 赏位似
18
谢谢聆听 欢迎指导!
