1.3 带电粒子在匀强磁场中的运动 能力提升(word版含答案)
文档属性
| 名称 | 1.3 带电粒子在匀强磁场中的运动 能力提升(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-08 08:54:30 | ||
图片预览


文档简介
1.3 带电粒子在匀强磁场中的运动 能力
一、单项选择题(共3小题;共12分)
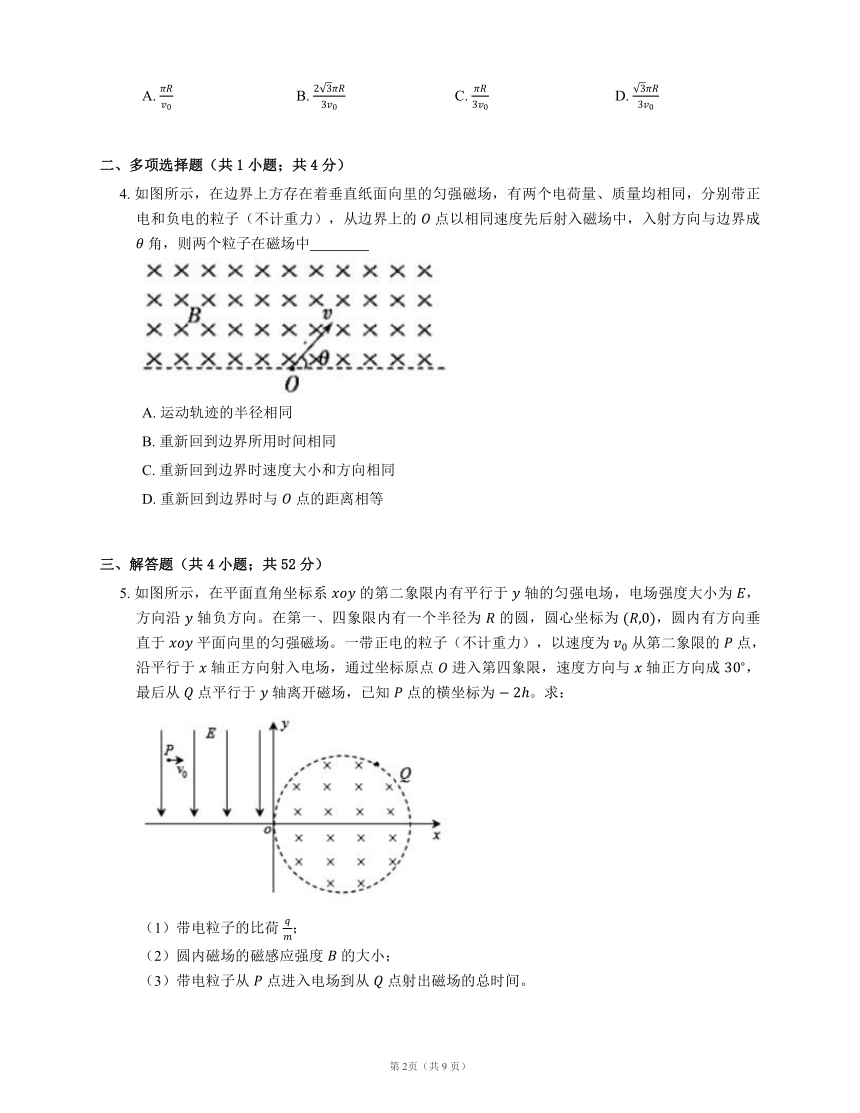
1. 如图所示,在直角三角形 区域(含边界)内存在垂直于纸面向外的匀强磁场,磁感应强度大小为 ,,,边长 。一个粒子源在 点将质量为 、电荷量为 的带正电粒子以大小和方向不同的速度射入磁场,在磁场中运动时间最长的粒子中,速度的最大值是
A. B. C. D.
2. 如图所示,矩形区域 长 ,宽 ,一质量为 (不计重力)、电荷量为 的带正电粒子从 点以初速度 水平向右射出,若区域内只存在竖直向下的电场或只存在垂直纸面向外的匀强磁场粒子均能击中 点,则电场强度 的大小与磁感应强度 的大小的比值为
A. B. C. D.
3. 半径为 的圆形区域内,存在着垂直纸面向里的匀强磁场,一个带负电的粒子(不计重力),从 点以速度 沿半径方向射入磁汤,并从 点射出,,如图所示,则带电粒子在磁场中运动的时间为
A. B. C. D.
二、多项选择题(共1小题;共4分)
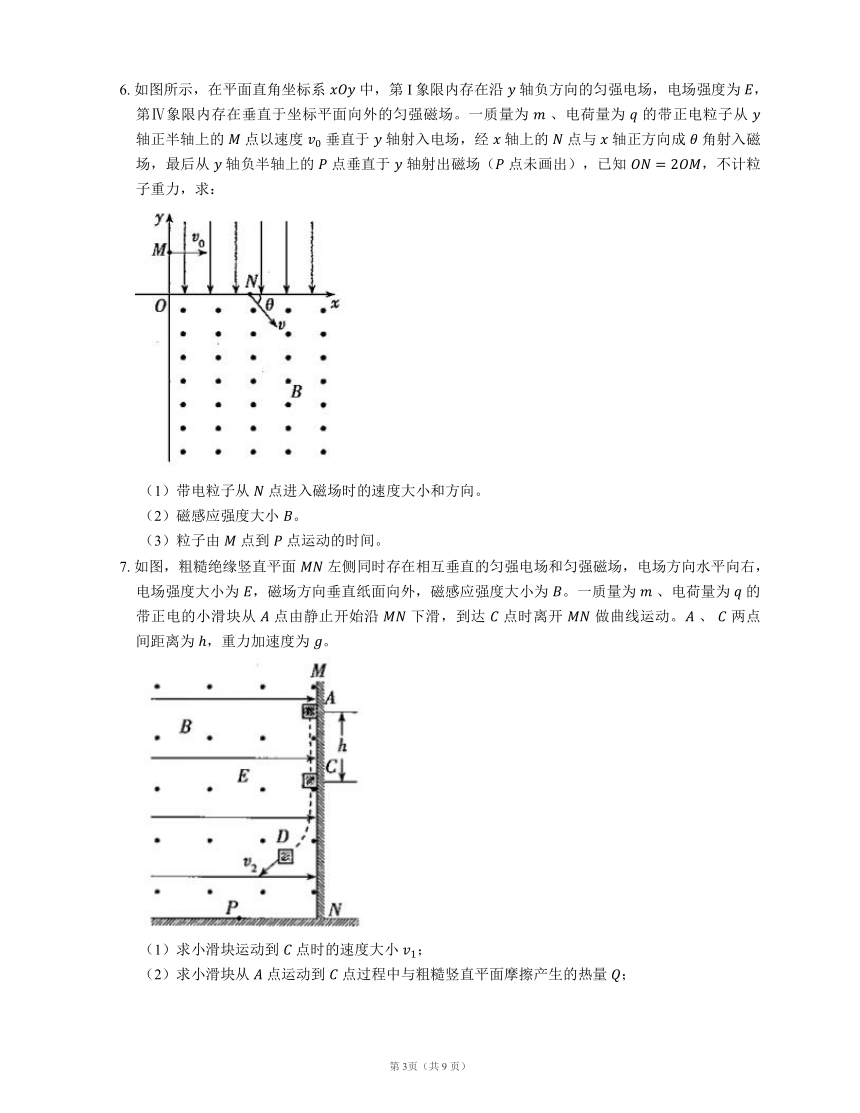
4. 如图所示,在边界上方存在着垂直纸面向里的匀强磁场,有两个电荷量、质量均相同,分别带正电和负电的粒子(不计重力),从边界上的 点以相同速度先后射入磁场中,入射方向与边界成 角,则两个粒子在磁场中
A. 运动轨迹的半径相同
B. 重新回到边界所用时间相同
C. 重新回到边界时速度大小和方向相同
D. 重新回到边界时与 点的距离相等
三、解答题(共4小题;共52分)
5. 如图所示,在平面直角坐标系 的第二象限内有平行于 轴的匀强电场,电场强度大小为 ,方向沿 轴负方向。在第一、四象限内有一个半径为 的圆,圆心坐标为 ,圆内有方向垂直于 平面向里的匀强磁场。一带正电的粒子(不计重力),以速度为 从第二象限的 点,沿平行于 轴正方向射入电场,通过坐标原点 进入第四象限,速度方向与 轴正方向成 ,最后从 点平行于 轴离开磁场,已知 点的横坐标为 。求:
(1)带电粒子的比荷 ;
(2)圆内磁场的磁感应强度 的大小;
(3)带电粒子从 点进入电场到从 点射出磁场的总时间。
6. 如图所示,在平面直角坐标系 中,第I象限内存在沿 轴负方向的匀强电场,电场强度为 ,第Ⅳ象限内存在垂直于坐标平面向外的匀强磁场。一质量为 、电荷量为 的带正电粒子从 轴正半轴上的 点以速度 垂直于 轴射入电场,经 轴上的 点与 轴正方向成 角射入磁场,最后从 轴负半轴上的 点垂直于 轴射出磁场( 点未画出),已知 ,不计粒子重力,求:
(1)带电粒子从 点进入磁场时的速度大小和方向。
(2)磁感应强度大小 。
(3)粒子由 点到 点运动的时间。
7. 如图,粗糙绝缘竖直平面 左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为 ,磁场方向垂直纸面向外,磁感应强度大小为 。一质量为 、电荷量为 的带正电的小滑块从 点由静止开始沿 下滑,到达 点时离开 做曲线运动。 、 两点间距离为 ,重力加速度为 。
(1)求小滑块运动到 点时的速度大小 ;
(2)求小滑块从 点运动到 点过程中与粗糙竖直平面摩擦产生的热量 ;
(3)若 点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到 点时撤去磁场,此后小滑块继续运动到水平地面上的 点。已知小滑块在 点时的速度大小为 ,从 点运动到 点的时间为 ,求小滑块运动到 点时的动能大小。
8. 如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为 。一绝缘“”形杆由两段直杆和一半径为 的半圆环组成,固定在纸面所在的竖直平面内, 、 水平且足够长,半圆环 在磁场边界左侧, 、 点在磁场界线上, 段是光滑的。现有一质量为 、带电荷量为 的小环套在 杆上,它所受到的电场力为重力的 。现从 右侧的 点由静止释放小环,小环刚好能到达 点。
(1)求 、 间的距离 ;
(2)求上述过程中小环第一次通过与 等高的 点时半圆环对小环作用力的大小;
(3)若小环与 间的动摩擦因数为 (设最大静摩擦力与滑动摩擦力大小相等),现将小环移至 点右侧 处由静止释放,求小环在整个运动过程中克服摩擦力所做的功。
答案
第一部分
1. A
【解析】根据题意可知,当粒子沿 方向射入并且运动轨迹与 相切时,粒子在磁场中的运动时间最长,速度最大,运动轨迹如图所示,设轨迹半径为 ,根据几何知识可知 ,,,则 ,,可得 ;由于 ,得到 ,选项A正确。
2. B
【解析】只有电场时,粒子做类平抛运动,水平方向有 ,竖直方向有 ,联立解得 。只有磁场时,粒子做匀速圆周运动,轨迹如图所示,结合几何关系,有 ,解得 ;洛伦兹力提供向心力,根据牛顿第二定律有 ,解得 ,故 ,选项B正确。
3. D
【解析】粒子在磁场中的运动轨迹如图所示,根据几何知识可知,粒子轨迹对应的圆心角为 ,轨迹半径为 ,粒子运动的弧长为 ,则粒子的运动时间 ,选项D正确,A、B、C错误。
第二部分
4. A, C, D
【解析】根据牛顿第二定律得 ,解得 ,由题知 、 、 、 大小均相同,则 相同,选项A正确。粒子的运动周期 ,由题知 、 、 大小均相同,则 相同;正、负两粒子的运动轨迹如图所示,带正电的粒子逆时针偏转,带负电的粒子顺时针偏转,重新回到边界时,带正电的粒子的速度偏向角为 ,轨迹对应的圆心角也为 ,运动时间为 ;同理,带负电的粒子运动时间为 ,时间不等,选项B错误。两个粒子在磁场中均做匀速圆周运动,速度沿轨迹的切线方向,根据对称性可知,两粒子重新回到边界时速度大小与方向均相同,选项C正确。根据几何知识得知,两粒子重新回到边界时与 点的距离均为 ,选项D正确。
第三部分
5. (1)
【解析】由水平方向匀速直线运动得
竖直向下的分速度
由竖直方向匀加速直线运动知
加速度为
根据以上式解得 ;
(2)
【解析】粒子进入磁场的速度为 ,有
由几何关系得,粒子在磁场中作匀速圆周运动的轨道半径为
由洛伦兹力提供向心力可知
解得 ;
(3)
【解析】粒子在磁场中运动的时间为
粒子在磁场中运动的周期为
粒子在电场中运动的时间为
粒子运动的总时
代入数据得:
6. (1) ;方向与 轴正方向成 角斜向下
【解析】带电粒子在电场中做类平抛运动,出电场时的速度的反向延长线经过水平位移的中点,由于 ,故有 ,则 ,。
(2)
【解析】带电粒子在复合场中的运动轨迹如图,
由几何关系可知轨迹半径 ,
带电粒子在电场中做类平抛运动,设运动时间为 ,
水平方向有 ,
竖直方向有 ,
联立解得 ,
带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有 ,
得 ,
其中 ,
联立解得 。
(3)
【解析】带电粒子出电场时,竖直方向的分速度为 ,
加速度 ,
得 ,
粒子在磁场中的运动周期 ,
粒子在磁场中的运动时间为 ,
联立解得 ,
所以总时间为 。
7. (1)
【解析】由题意知,当洛伦兹力等于电场力时,小滑块即将离开竖直平面 ,有
解得 。
(2)
【解析】小滑块从 到 过程,根据能量守恒定律得
解得 。
(3)
【解析】设重力与电场力的合力为 ,由题意知,在 点时速度 的方向与 的方向垂直。撤去磁场后,小滑块从 到 做类平抛运动,在力 方向上,滑块做匀加速直线运动,有
力 方向即垂直于 方向的位移
根据动能定理有
又知
联立解得 。
8. (1)
【解析】小环从 点到 点的过程中,由动能定理得
已知
得 。
(2)
【解析】设小环在 点时速度为 ,小环从 点到 点过程中,由动能定理得
得
在 点,由牛顿第二定律得
解得 。
(3) 或
【解析】若 即 ,小环到达 点右侧距 处静止,则有
得
所以小环克服摩擦力做功
若 即 小环经过往复运动,最后只能在 、 之间运动
运动,则有
得 。
第1页(共1 页)
一、单项选择题(共3小题;共12分)
1. 如图所示,在直角三角形 区域(含边界)内存在垂直于纸面向外的匀强磁场,磁感应强度大小为 ,,,边长 。一个粒子源在 点将质量为 、电荷量为 的带正电粒子以大小和方向不同的速度射入磁场,在磁场中运动时间最长的粒子中,速度的最大值是
A. B. C. D.
2. 如图所示,矩形区域 长 ,宽 ,一质量为 (不计重力)、电荷量为 的带正电粒子从 点以初速度 水平向右射出,若区域内只存在竖直向下的电场或只存在垂直纸面向外的匀强磁场粒子均能击中 点,则电场强度 的大小与磁感应强度 的大小的比值为
A. B. C. D.
3. 半径为 的圆形区域内,存在着垂直纸面向里的匀强磁场,一个带负电的粒子(不计重力),从 点以速度 沿半径方向射入磁汤,并从 点射出,,如图所示,则带电粒子在磁场中运动的时间为
A. B. C. D.
二、多项选择题(共1小题;共4分)
4. 如图所示,在边界上方存在着垂直纸面向里的匀强磁场,有两个电荷量、质量均相同,分别带正电和负电的粒子(不计重力),从边界上的 点以相同速度先后射入磁场中,入射方向与边界成 角,则两个粒子在磁场中
A. 运动轨迹的半径相同
B. 重新回到边界所用时间相同
C. 重新回到边界时速度大小和方向相同
D. 重新回到边界时与 点的距离相等
三、解答题(共4小题;共52分)
5. 如图所示,在平面直角坐标系 的第二象限内有平行于 轴的匀强电场,电场强度大小为 ,方向沿 轴负方向。在第一、四象限内有一个半径为 的圆,圆心坐标为 ,圆内有方向垂直于 平面向里的匀强磁场。一带正电的粒子(不计重力),以速度为 从第二象限的 点,沿平行于 轴正方向射入电场,通过坐标原点 进入第四象限,速度方向与 轴正方向成 ,最后从 点平行于 轴离开磁场,已知 点的横坐标为 。求:
(1)带电粒子的比荷 ;
(2)圆内磁场的磁感应强度 的大小;
(3)带电粒子从 点进入电场到从 点射出磁场的总时间。
6. 如图所示,在平面直角坐标系 中,第I象限内存在沿 轴负方向的匀强电场,电场强度为 ,第Ⅳ象限内存在垂直于坐标平面向外的匀强磁场。一质量为 、电荷量为 的带正电粒子从 轴正半轴上的 点以速度 垂直于 轴射入电场,经 轴上的 点与 轴正方向成 角射入磁场,最后从 轴负半轴上的 点垂直于 轴射出磁场( 点未画出),已知 ,不计粒子重力,求:
(1)带电粒子从 点进入磁场时的速度大小和方向。
(2)磁感应强度大小 。
(3)粒子由 点到 点运动的时间。
7. 如图,粗糙绝缘竖直平面 左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为 ,磁场方向垂直纸面向外,磁感应强度大小为 。一质量为 、电荷量为 的带正电的小滑块从 点由静止开始沿 下滑,到达 点时离开 做曲线运动。 、 两点间距离为 ,重力加速度为 。
(1)求小滑块运动到 点时的速度大小 ;
(2)求小滑块从 点运动到 点过程中与粗糙竖直平面摩擦产生的热量 ;
(3)若 点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到 点时撤去磁场,此后小滑块继续运动到水平地面上的 点。已知小滑块在 点时的速度大小为 ,从 点运动到 点的时间为 ,求小滑块运动到 点时的动能大小。
8. 如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为 。一绝缘“”形杆由两段直杆和一半径为 的半圆环组成,固定在纸面所在的竖直平面内, 、 水平且足够长,半圆环 在磁场边界左侧, 、 点在磁场界线上, 段是光滑的。现有一质量为 、带电荷量为 的小环套在 杆上,它所受到的电场力为重力的 。现从 右侧的 点由静止释放小环,小环刚好能到达 点。
(1)求 、 间的距离 ;
(2)求上述过程中小环第一次通过与 等高的 点时半圆环对小环作用力的大小;
(3)若小环与 间的动摩擦因数为 (设最大静摩擦力与滑动摩擦力大小相等),现将小环移至 点右侧 处由静止释放,求小环在整个运动过程中克服摩擦力所做的功。
答案
第一部分
1. A
【解析】根据题意可知,当粒子沿 方向射入并且运动轨迹与 相切时,粒子在磁场中的运动时间最长,速度最大,运动轨迹如图所示,设轨迹半径为 ,根据几何知识可知 ,,,则 ,,可得 ;由于 ,得到 ,选项A正确。
2. B
【解析】只有电场时,粒子做类平抛运动,水平方向有 ,竖直方向有 ,联立解得 。只有磁场时,粒子做匀速圆周运动,轨迹如图所示,结合几何关系,有 ,解得 ;洛伦兹力提供向心力,根据牛顿第二定律有 ,解得 ,故 ,选项B正确。
3. D
【解析】粒子在磁场中的运动轨迹如图所示,根据几何知识可知,粒子轨迹对应的圆心角为 ,轨迹半径为 ,粒子运动的弧长为 ,则粒子的运动时间 ,选项D正确,A、B、C错误。
第二部分
4. A, C, D
【解析】根据牛顿第二定律得 ,解得 ,由题知 、 、 、 大小均相同,则 相同,选项A正确。粒子的运动周期 ,由题知 、 、 大小均相同,则 相同;正、负两粒子的运动轨迹如图所示,带正电的粒子逆时针偏转,带负电的粒子顺时针偏转,重新回到边界时,带正电的粒子的速度偏向角为 ,轨迹对应的圆心角也为 ,运动时间为 ;同理,带负电的粒子运动时间为 ,时间不等,选项B错误。两个粒子在磁场中均做匀速圆周运动,速度沿轨迹的切线方向,根据对称性可知,两粒子重新回到边界时速度大小与方向均相同,选项C正确。根据几何知识得知,两粒子重新回到边界时与 点的距离均为 ,选项D正确。
第三部分
5. (1)
【解析】由水平方向匀速直线运动得
竖直向下的分速度
由竖直方向匀加速直线运动知
加速度为
根据以上式解得 ;
(2)
【解析】粒子进入磁场的速度为 ,有
由几何关系得,粒子在磁场中作匀速圆周运动的轨道半径为
由洛伦兹力提供向心力可知
解得 ;
(3)
【解析】粒子在磁场中运动的时间为
粒子在磁场中运动的周期为
粒子在电场中运动的时间为
粒子运动的总时
代入数据得:
6. (1) ;方向与 轴正方向成 角斜向下
【解析】带电粒子在电场中做类平抛运动,出电场时的速度的反向延长线经过水平位移的中点,由于 ,故有 ,则 ,。
(2)
【解析】带电粒子在复合场中的运动轨迹如图,
由几何关系可知轨迹半径 ,
带电粒子在电场中做类平抛运动,设运动时间为 ,
水平方向有 ,
竖直方向有 ,
联立解得 ,
带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有 ,
得 ,
其中 ,
联立解得 。
(3)
【解析】带电粒子出电场时,竖直方向的分速度为 ,
加速度 ,
得 ,
粒子在磁场中的运动周期 ,
粒子在磁场中的运动时间为 ,
联立解得 ,
所以总时间为 。
7. (1)
【解析】由题意知,当洛伦兹力等于电场力时,小滑块即将离开竖直平面 ,有
解得 。
(2)
【解析】小滑块从 到 过程,根据能量守恒定律得
解得 。
(3)
【解析】设重力与电场力的合力为 ,由题意知,在 点时速度 的方向与 的方向垂直。撤去磁场后,小滑块从 到 做类平抛运动,在力 方向上,滑块做匀加速直线运动,有
力 方向即垂直于 方向的位移
根据动能定理有
又知
联立解得 。
8. (1)
【解析】小环从 点到 点的过程中,由动能定理得
已知
得 。
(2)
【解析】设小环在 点时速度为 ,小环从 点到 点过程中,由动能定理得
得
在 点,由牛顿第二定律得
解得 。
(3) 或
【解析】若 即 ,小环到达 点右侧距 处静止,则有
得
所以小环克服摩擦力做功
若 即 小环经过往复运动,最后只能在 、 之间运动
运动,则有
得 。
第1页(共1 页)
