陕西省咸阳市三原县城关北城高级中学2021-2022学年高二上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 陕西省咸阳市三原县城关北城高级中学2021-2022学年高二上学期12月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-08 14:48:10 | ||
图片预览



文档简介
三原县城关北城高级中学2021-2022学年高二上学期12月月考
数学试卷
一、单选题
1.已知定义在R上的函数 满足 , 为 的导函数,且导函数 的图象如图所示,则不等式 的解集是( )
A. (-3,0) B. (-3,5) C. (0,5) D. (-∞,-3)∪(5,+∞)
2.在 中,角A,B,C的对边分别为a,b,c,且 , , ,则
A. B. C. 或 D. 或
3.已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16, 其中第一项是 ,接下来的两项是 , ,再接下来的三项是 , , ,依此类推那么该数列的前50项和为
A. 1044 B. 1024 C. 1045 D. 1025
4.已知全集U=R,集合M={x|x2+2x﹣3≥0},N={x|log2x≤1},则( UM)∪N=( )
A. {x|﹣1≤x≤2} B. {x|﹣1≤x≤3} C. {x|﹣3<x≤2} D. {x|0<x<1}
5.下列命题中真命题的个数是( )
中, 是 的三内角A,B,C成等差数列的充要条件; 若“ ,则 ”的逆命题为真命题; 是 或 充分不必要条件; 是 的充要条件.
A. 1个 B. 2个 C. 3个 D. 4个
6.已知当 时,函数 的图象与 的图象有且只有一个交点,则正实数 的取值范围是 ( )
A. B. C. D.
7.求函数 的值域( )
A. [0,+∞) B. [ ,+∞) C. [ ,+∞) D. [ ,+∞)
8.已知△ABC的重心为G,角A,B,C所对的边分别为 ,若 ,则 ( )
A. B. C. D.
9.已知点 , .若点 在抛物线 上,则使得 的面积为2的点 的个数为( )
A. 1 B. 2 C. 3 D. 4
10.在长方体 中,底面 是边长为1的正方形,异面直线 与 所成角的大小为 ,则该长方体的表面积与体积的比值是( )
A.
B.
C.
D.
11.直线 与圆 相交于 两点,若 ,则 的取值范围是( )
A. B. C. D. (-2 , -2)∪[2,2)
12.设函数 ,其中 ,若有且只有一个整数 使得 ,则 的取值范围是( )
A. B. C. D.
13.由直线 上的点P向圆C: 引切线PT(T为切点),当|PT|最小时,点P的坐标是( )
A. (-1,1) B. (0,2) C. (-2,0) D. (1,3)
14.下列说法正确的是( )
A. “ ”是“ ”的必要不充分条件
B. 命题“ ”的否定是“ ”
C. 若 ,则 是真命题
D. 若 ,则实数 的取值范围是
15.如图,在正方体 中, 分别是 的中点,则下列判断错误的是( )
A. B. C. D.
16.以 和 为端点的线段 的垂直平分线方程是( )
A. B. C. D.
17.以下选项正确的是( )
A. 是 的充分条件 B. 是 的必要条件
C. 是 的必要条件 D. 是 的充要条件
18.若 ,且 则实数 的值是( )
A. B. 0 C. 1 D.
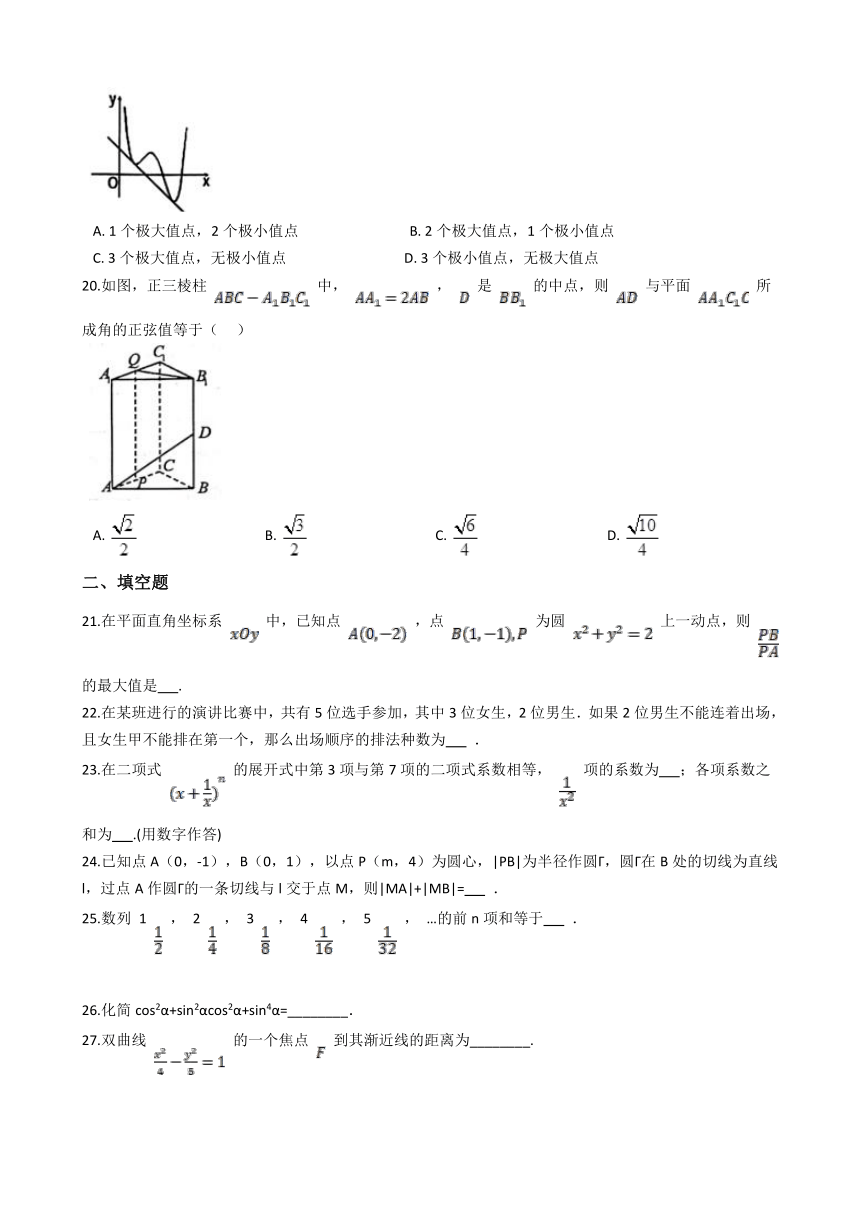
19.如图,已知直线 与曲线 相切于两点,则 有( )
A. 1个极大值点,2个极小值点 B. 2个极大值点,1个极小值点
C. 3个极大值点,无极小值点 D. 3个极小值点,无极大值点
20.如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( )
A. B. C. D.
二、填空题
21.在平面直角坐标系 中,已知点 ,点 为圆 上一动点,则 的最大值是 .
22.在某班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连着出场,且女生甲不能排在第一个,那么出场顺序的排法种数为 .
23.在二项式 的展开式中第3项与第7项的二项式系数相等, 项的系数为 ;各项系数之和为 .(用数字作答)
24.已知点A(0,-1),B(0,1),以点P(m,4)为圆心,|PB|为半径作圆Γ,圆Γ在B处的切线为直线l,过点A作圆Γ的一条切线与l交于点M,则|MA|+|MB|= .
25.数列 1 , 2 , 3 , 4 , 5 , …的前n项和等于 .
26.化简cos2α+sin2αcos2α+sin4α=________.
27.双曲线 的一个焦点 到其渐近线的距离为________.
28.在△ABC中,角A,B,C所对应的边分别为a,b,c,已知b=1,c=2且2cosA(bcosC+ccosB)=a,则A= ;若M为边BC的中点,则|AM|=
29.cos150°=________.
30.已知函数f(x)=xlnx,且0<x1<x2 , 给出下列命题:
① <1
②x2f(x1)<x1f(x2)
③当lnx>﹣1时,x1f(x1)+x2f(x2)>2x2f(x1)
④x1+f(x1)<x2+f(x2)
其中正确的命题序号是 .
三、解答题
31.已知椭圆 的中心在原点,焦点在 轴上,其长轴长为 ,短轴长与焦距相等.
(1)求椭圆 的标准方程;
(2)若斜率为1的直线 与椭圆交于 两点且 ,求直线 的方程.
32.设抛物线 : , 为 的焦点,过 的直线 与 相交于 两点.
(1)设 的斜率为1,求 ;
(2)求证: 是一个定值.
33.在 的展开式中
(1)求含 的项;
(2)求各项系数和与各项二项式系数和的比.
34.已知点M(0,3),N(-4,0)及点P(-2,4);
(1)若直线l经过点P且l MN,求直线l的方程;
(2)求△MNP的面积.
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 D
3.【答案】 A
4.【答案】 C
5.【答案】 B
6.【答案】 B
7.【答案】 D
8.【答案】 B
9.【答案】 D
10.【答案】 D
11.【答案】 A
12.【答案】 D
13.【答案】 B
14.【答案】 D
15.【答案】 D
16.【答案】 A
17.【答案】 B
18.【答案】 D
19.【答案】 A
20.【答案】 C
二、填空题
21.【答案】 2
22.【答案】 60
23.【答案】 56;256
24.【答案】 4
25.【答案】
26.【答案】1
27.【答案】
28.【答案】 ;
29.【答案】
30.【答案】 ②③
三、解答题
31.【答案】 (1)解:由题知, ,由 ,且
解得 ,
又椭圆的焦点在 轴上,
所以椭圆的标准方程为
(2)解:设直线 的方程为 ,
设
联立
得:
且 , ①
因为 ,
所以
又 ,
因此得 ,
则 ②
将①代入②得:
解得 符合题意
因此直线 的方程为
即 或
32.【答案】 (1)解:∵由题意可知抛物线的焦点 为 ,准线方程为 ,
∴直线 的方程为
设 ,由
得 ,
∴ ,
由直线 过焦点,则 .
(2)证明:设直线 的方程为 ,
由 得
∴ ,
,
∵ ,
,
∴ 是一个定值.
33.【答案】 (1)解:由题意知 ,
令 得 ,
所以含 的项为
(2)解:令 得各项系数和为 ,
又由题意知各项二项式系数和为 ,
所以 ,
所以各项系数和与各项二项式系数和的比为 .
34.【答案】 (1)解:由题意可得: ,
直线 的方程为 ,即
则直线l的方程为
(2)解:由题意可得直线MN的方程为: ,即 ,
点P到直线MN的距离为 ,
,
△MNP的面积
△MNP的面积为5
数学试卷
一、单选题
1.已知定义在R上的函数 满足 , 为 的导函数,且导函数 的图象如图所示,则不等式 的解集是( )
A. (-3,0) B. (-3,5) C. (0,5) D. (-∞,-3)∪(5,+∞)
2.在 中,角A,B,C的对边分别为a,b,c,且 , , ,则
A. B. C. 或 D. 或
3.已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16, 其中第一项是 ,接下来的两项是 , ,再接下来的三项是 , , ,依此类推那么该数列的前50项和为
A. 1044 B. 1024 C. 1045 D. 1025
4.已知全集U=R,集合M={x|x2+2x﹣3≥0},N={x|log2x≤1},则( UM)∪N=( )
A. {x|﹣1≤x≤2} B. {x|﹣1≤x≤3} C. {x|﹣3<x≤2} D. {x|0<x<1}
5.下列命题中真命题的个数是( )
中, 是 的三内角A,B,C成等差数列的充要条件; 若“ ,则 ”的逆命题为真命题; 是 或 充分不必要条件; 是 的充要条件.
A. 1个 B. 2个 C. 3个 D. 4个
6.已知当 时,函数 的图象与 的图象有且只有一个交点,则正实数 的取值范围是 ( )
A. B. C. D.
7.求函数 的值域( )
A. [0,+∞) B. [ ,+∞) C. [ ,+∞) D. [ ,+∞)
8.已知△ABC的重心为G,角A,B,C所对的边分别为 ,若 ,则 ( )
A. B. C. D.
9.已知点 , .若点 在抛物线 上,则使得 的面积为2的点 的个数为( )
A. 1 B. 2 C. 3 D. 4
10.在长方体 中,底面 是边长为1的正方形,异面直线 与 所成角的大小为 ,则该长方体的表面积与体积的比值是( )
A.
B.
C.
D.
11.直线 与圆 相交于 两点,若 ,则 的取值范围是( )
A. B. C. D. (-2 , -2)∪[2,2)
12.设函数 ,其中 ,若有且只有一个整数 使得 ,则 的取值范围是( )
A. B. C. D.
13.由直线 上的点P向圆C: 引切线PT(T为切点),当|PT|最小时,点P的坐标是( )
A. (-1,1) B. (0,2) C. (-2,0) D. (1,3)
14.下列说法正确的是( )
A. “ ”是“ ”的必要不充分条件
B. 命题“ ”的否定是“ ”
C. 若 ,则 是真命题
D. 若 ,则实数 的取值范围是
15.如图,在正方体 中, 分别是 的中点,则下列判断错误的是( )
A. B. C. D.
16.以 和 为端点的线段 的垂直平分线方程是( )
A. B. C. D.
17.以下选项正确的是( )
A. 是 的充分条件 B. 是 的必要条件
C. 是 的必要条件 D. 是 的充要条件
18.若 ,且 则实数 的值是( )
A. B. 0 C. 1 D.
19.如图,已知直线 与曲线 相切于两点,则 有( )
A. 1个极大值点,2个极小值点 B. 2个极大值点,1个极小值点
C. 3个极大值点,无极小值点 D. 3个极小值点,无极大值点
20.如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( )
A. B. C. D.
二、填空题
21.在平面直角坐标系 中,已知点 ,点 为圆 上一动点,则 的最大值是 .
22.在某班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连着出场,且女生甲不能排在第一个,那么出场顺序的排法种数为 .
23.在二项式 的展开式中第3项与第7项的二项式系数相等, 项的系数为 ;各项系数之和为 .(用数字作答)
24.已知点A(0,-1),B(0,1),以点P(m,4)为圆心,|PB|为半径作圆Γ,圆Γ在B处的切线为直线l,过点A作圆Γ的一条切线与l交于点M,则|MA|+|MB|= .
25.数列 1 , 2 , 3 , 4 , 5 , …的前n项和等于 .
26.化简cos2α+sin2αcos2α+sin4α=________.
27.双曲线 的一个焦点 到其渐近线的距离为________.
28.在△ABC中,角A,B,C所对应的边分别为a,b,c,已知b=1,c=2且2cosA(bcosC+ccosB)=a,则A= ;若M为边BC的中点,则|AM|=
29.cos150°=________.
30.已知函数f(x)=xlnx,且0<x1<x2 , 给出下列命题:
① <1
②x2f(x1)<x1f(x2)
③当lnx>﹣1时,x1f(x1)+x2f(x2)>2x2f(x1)
④x1+f(x1)<x2+f(x2)
其中正确的命题序号是 .
三、解答题
31.已知椭圆 的中心在原点,焦点在 轴上,其长轴长为 ,短轴长与焦距相等.
(1)求椭圆 的标准方程;
(2)若斜率为1的直线 与椭圆交于 两点且 ,求直线 的方程.
32.设抛物线 : , 为 的焦点,过 的直线 与 相交于 两点.
(1)设 的斜率为1,求 ;
(2)求证: 是一个定值.
33.在 的展开式中
(1)求含 的项;
(2)求各项系数和与各项二项式系数和的比.
34.已知点M(0,3),N(-4,0)及点P(-2,4);
(1)若直线l经过点P且l MN,求直线l的方程;
(2)求△MNP的面积.
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 D
3.【答案】 A
4.【答案】 C
5.【答案】 B
6.【答案】 B
7.【答案】 D
8.【答案】 B
9.【答案】 D
10.【答案】 D
11.【答案】 A
12.【答案】 D
13.【答案】 B
14.【答案】 D
15.【答案】 D
16.【答案】 A
17.【答案】 B
18.【答案】 D
19.【答案】 A
20.【答案】 C
二、填空题
21.【答案】 2
22.【答案】 60
23.【答案】 56;256
24.【答案】 4
25.【答案】
26.【答案】1
27.【答案】
28.【答案】 ;
29.【答案】
30.【答案】 ②③
三、解答题
31.【答案】 (1)解:由题知, ,由 ,且
解得 ,
又椭圆的焦点在 轴上,
所以椭圆的标准方程为
(2)解:设直线 的方程为 ,
设
联立
得:
且 , ①
因为 ,
所以
又 ,
因此得 ,
则 ②
将①代入②得:
解得 符合题意
因此直线 的方程为
即 或
32.【答案】 (1)解:∵由题意可知抛物线的焦点 为 ,准线方程为 ,
∴直线 的方程为
设 ,由
得 ,
∴ ,
由直线 过焦点,则 .
(2)证明:设直线 的方程为 ,
由 得
∴ ,
,
∵ ,
,
∴ 是一个定值.
33.【答案】 (1)解:由题意知 ,
令 得 ,
所以含 的项为
(2)解:令 得各项系数和为 ,
又由题意知各项二项式系数和为 ,
所以 ,
所以各项系数和与各项二项式系数和的比为 .
34.【答案】 (1)解:由题意可得: ,
直线 的方程为 ,即
则直线l的方程为
(2)解:由题意可得直线MN的方程为: ,即 ,
点P到直线MN的距离为 ,
,
△MNP的面积
△MNP的面积为5
同课章节目录
