沪科版数学八年级上册 15.2 线段的垂直平分线 课件(共21张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.2 线段的垂直平分线 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 523.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 09:30:04 | ||
图片预览





文档简介
(共21张PPT)
15.2 线段的垂直平分线
操作
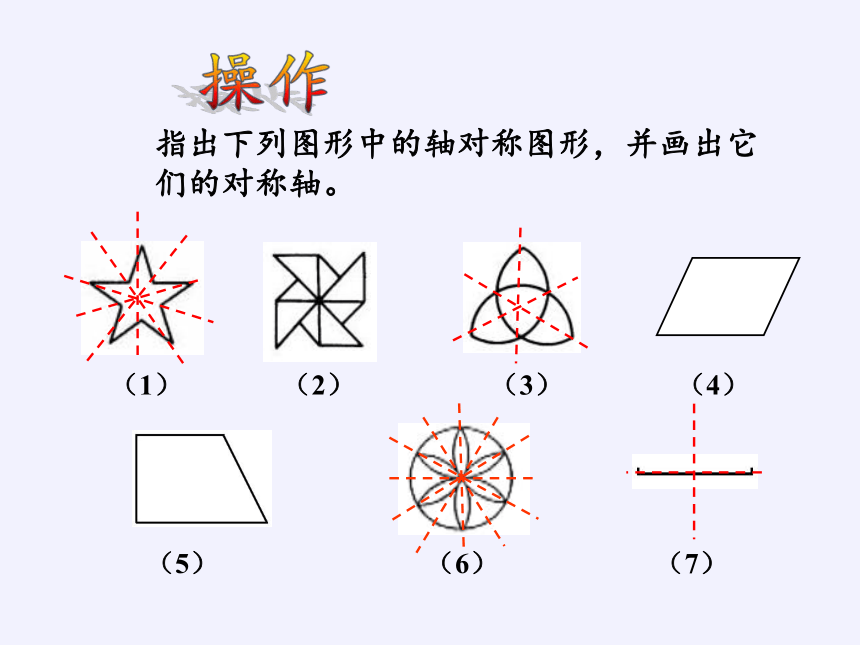
指出下列图形中的轴对称图形,并画出它们的对称轴。
(1) (2) (3) (4)
(5) (6) (7)
问题
怎样做出一条线段的垂直平分线?
2. 过点E、F作直线。
1. 分别以点A、B为圆心,大于
长为半径,画弧
交于点E、F;
尺规作图
作法:
3. 则直线EF就是线段AB的垂直平分线
线段垂直平分线上的点与线段两端的距离相等。
探究
测量
猜想
证明
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
已知,如图,直线MN经过线段AB的中点O,且MN⊥AB,P是MN上
任意一点。求证:
解:∵直线MN经过线段AB的中点O
∴AO=BO
又∵MN⊥AB
∴∠POA=∠POB=90°
在△POA与△POB中
AO=BO
∠POA=∠POB
PO=OP
∴△POA≌△POB(SAS)
∴PA=PB
{
线段垂直平分线上的点与线段两端的距离相等。
线段垂直平分线上的点到线段两端的距离相等。
探究
测量
猜想
证明
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
定理
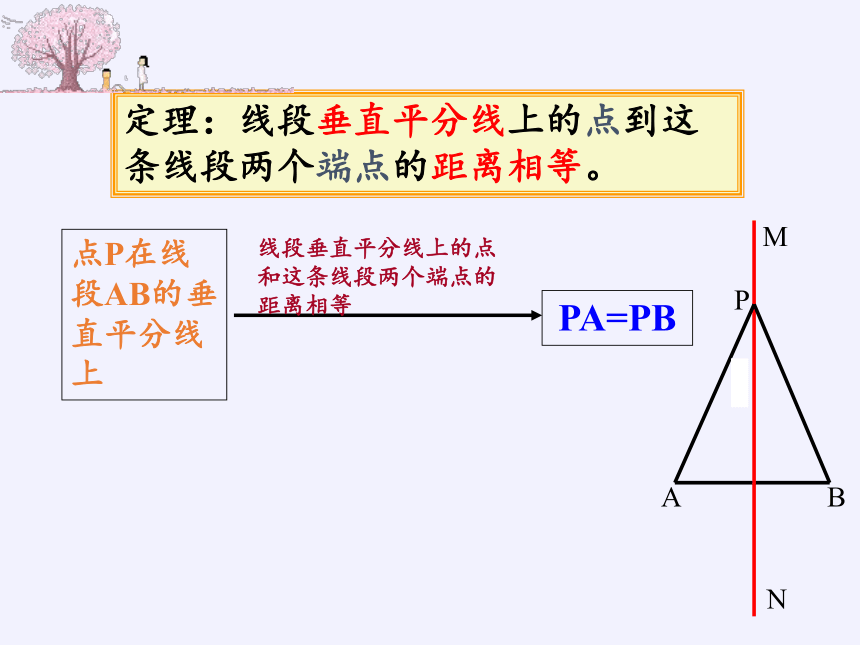
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点和这条线段两个端点的距离相等
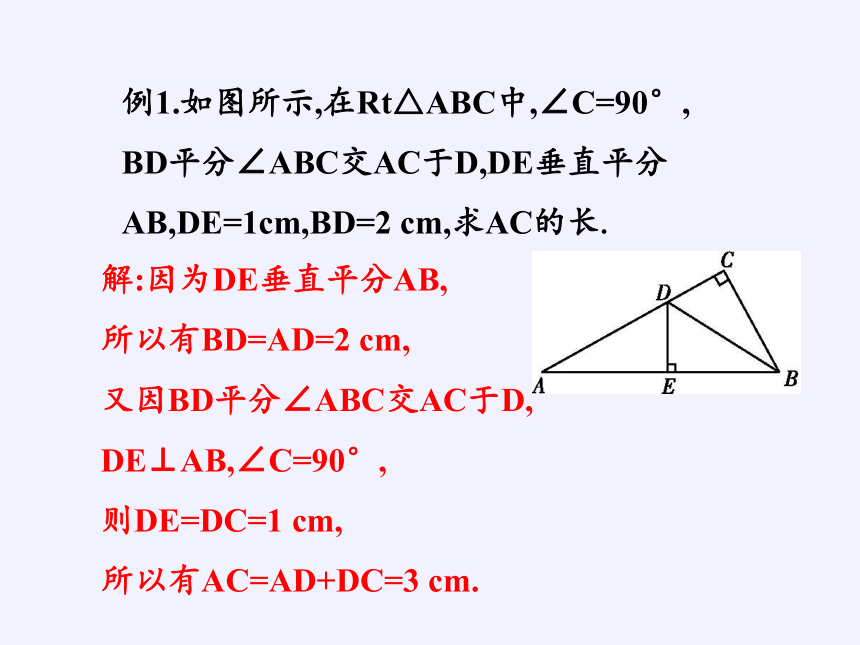
例1.如图所示,在Rt△ABC中,∠C=90°,
BD平分∠ABC交AC于D,DE垂直平分AB,DE=1cm,BD=2 cm,求AC的长.
解:因为DE垂直平分AB,
所以有BD=AD=2 cm,
又因BD平分∠ABC交AC于D,
DE⊥AB,∠C=90°,
则DE=DC=1 cm,
所以有AC=AD+DC=3 cm.
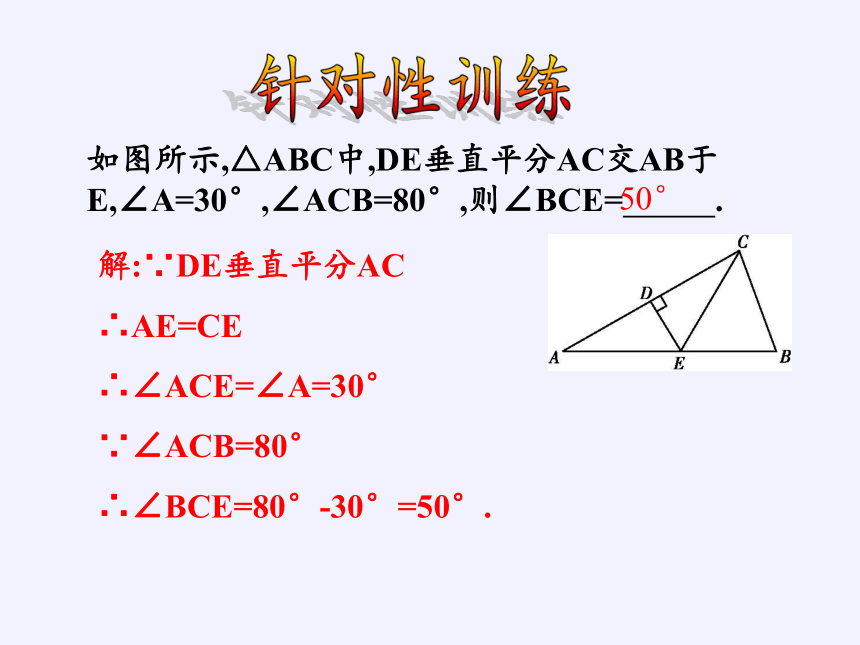
如图所示,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= .
解:∵DE垂直平分AC
∴AE=CE
∴∠ACE=∠A=30°
∵∠ACB=80°
∴∠BCE=80°-30°=50°.
50°
针对性训练
例2 已知:如图,AB=AC=8cm ,DE是AB边的中垂线交AC于点E,BC=6cm,求△BEC的周长
证明: ∵ DE是AB边的中垂线 (已知),
∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴AE+EC=BE+EC=8cm
(等式性质).
∵AC=8cm(已知),
∴ C△BEC=BE+EC+BC
=8+6=14cm
又∵ BC=6cm(已知)
有垂直平分线,就有等腰三角形的产生
C
解析:由MN是AB的垂直平分线得AD=BD,
由△ADC的周长为10,
得AC+BC=AC+AD+CD=10,
∴△ABC的周长为AC+BC+AB=10+7=17.
故选C.
针对性训练
A
B
L
实际问题
在国道L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
105 国 道
L
思考
你能写出上述定理的逆命题吗?它是真命题吗?
线段垂直平分线上的点到线段两端的距离相等。
定理
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
逆命题:到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
点P在线段AB的垂直平分线上
PA=PB
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
求证:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
已知:如图,PA=PB
求证:P在AB的垂直平分线上
证明:过P点作MN⊥AB,垂足为C
∵PA=PB(已知)
∴AC=BC
(等腰三角形的“三线合一”)
A
B
P
M
N
C
∴ MN是AB的垂直平分线
∴P在AB的垂直平分线上
定理
到线段两端距离相等的点在这条线段的垂直平分线上。
A
B
C
M
N
例3、已知: ABC中, C=90 , A=30 ,
BD平分 ABC交AC于D.
求证:D点在AB的垂直平分线上.
A
B
C
D
证明:
30
∵ C=90 , A=30 (已知)
∴ ABC=60 (三角形内角和定理)
∴ A= ABD (等量代换)
∴ D点在AB的垂直平分线上.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.)
∵BD平分 A BC(已知)
∴ ABD=30 (角平分线的定义)
∴ AD=BD(等角对等边)
30
整理小结
与线段两端距离相等的点在这条线段的垂直平分线上。
一种作图
尺规作图法
一个方法
证明线段相等的新方法:利用线段垂直平分线的性质。
两个定理
线段垂直平分线上的点与线段两端的距离相等。
作业布置
(1)课本:习题15.2 第3、4题
(2)点拨 15.2节
谢 谢
15.2 线段的垂直平分线
操作
指出下列图形中的轴对称图形,并画出它们的对称轴。
(1) (2) (3) (4)
(5) (6) (7)
问题
怎样做出一条线段的垂直平分线?
2. 过点E、F作直线。
1. 分别以点A、B为圆心,大于
长为半径,画弧
交于点E、F;
尺规作图
作法:
3. 则直线EF就是线段AB的垂直平分线
线段垂直平分线上的点与线段两端的距离相等。
探究
测量
猜想
证明
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
已知,如图,直线MN经过线段AB的中点O,且MN⊥AB,P是MN上
任意一点。求证:
解:∵直线MN经过线段AB的中点O
∴AO=BO
又∵MN⊥AB
∴∠POA=∠POB=90°
在△POA与△POB中
AO=BO
∠POA=∠POB
PO=OP
∴△POA≌△POB(SAS)
∴PA=PB
{
线段垂直平分线上的点与线段两端的距离相等。
线段垂直平分线上的点到线段两端的距离相等。
探究
测量
猜想
证明
测量线段垂直平分线上任意一点到线段两个端点的距离
已知,如图,直线MN经过线段AB的
中点O,且MN⊥AB,P是MN上
任意一点。
求证:
定理
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
A
B
P
M
N
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点和这条线段两个端点的距离相等
例1.如图所示,在Rt△ABC中,∠C=90°,
BD平分∠ABC交AC于D,DE垂直平分AB,DE=1cm,BD=2 cm,求AC的长.
解:因为DE垂直平分AB,
所以有BD=AD=2 cm,
又因BD平分∠ABC交AC于D,
DE⊥AB,∠C=90°,
则DE=DC=1 cm,
所以有AC=AD+DC=3 cm.
如图所示,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= .
解:∵DE垂直平分AC
∴AE=CE
∴∠ACE=∠A=30°
∵∠ACB=80°
∴∠BCE=80°-30°=50°.
50°
针对性训练
例2 已知:如图,AB=AC=8cm ,DE是AB边的中垂线交AC于点E,BC=6cm,求△BEC的周长
证明: ∵ DE是AB边的中垂线 (已知),
∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴AE+EC=BE+EC=8cm
(等式性质).
∵AC=8cm(已知),
∴ C△BEC=BE+EC+BC
=8+6=14cm
又∵ BC=6cm(已知)
有垂直平分线,就有等腰三角形的产生
C
解析:由MN是AB的垂直平分线得AD=BD,
由△ADC的周长为10,
得AC+BC=AC+AD+CD=10,
∴△ABC的周长为AC+BC+AB=10+7=17.
故选C.
针对性训练
A
B
L
实际问题
在国道L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
105 国 道
L
思考
你能写出上述定理的逆命题吗?它是真命题吗?
线段垂直平分线上的点到线段两端的距离相等。
定理
定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
逆命题:到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
点P在线段AB的垂直平分线上
PA=PB
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
求证:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
已知:如图,PA=PB
求证:P在AB的垂直平分线上
证明:过P点作MN⊥AB,垂足为C
∵PA=PB(已知)
∴AC=BC
(等腰三角形的“三线合一”)
A
B
P
M
N
C
∴ MN是AB的垂直平分线
∴P在AB的垂直平分线上
定理
到线段两端距离相等的点在这条线段的垂直平分线上。
A
B
C
M
N
例3、已知: ABC中, C=90 , A=30 ,
BD平分 ABC交AC于D.
求证:D点在AB的垂直平分线上.
A
B
C
D
证明:
30
∵ C=90 , A=30 (已知)
∴ ABC=60 (三角形内角和定理)
∴ A= ABD (等量代换)
∴ D点在AB的垂直平分线上.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.)
∵BD平分 A BC(已知)
∴ ABD=30 (角平分线的定义)
∴ AD=BD(等角对等边)
30
整理小结
与线段两端距离相等的点在这条线段的垂直平分线上。
一种作图
尺规作图法
一个方法
证明线段相等的新方法:利用线段垂直平分线的性质。
两个定理
线段垂直平分线上的点与线段两端的距离相等。
作业布置
(1)课本:习题15.2 第3、4题
(2)点拨 15.2节
谢 谢
