高中数学人教新课标A版必修5 1.1 正弦定理和余弦定理(word含答案解析)
文档属性
| 名称 | 高中数学人教新课标A版必修5 1.1 正弦定理和余弦定理(word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 00:00:00 | ||
图片预览


文档简介
1.1 正弦定理和余弦定理
一、选择题(共10小题;共50分)
1. 在 中,角 ,, 所对的边分别为 ,,,若 ,,,则 的面积 等于
A. B. C. D.
2. 的内角 ,, 的对边分别为 ,,,若 的面积为 ,则
A. B. C. D.
3. 设在 中,角 ,, 所对的边分别为 ,,,若 ,则 的形状为
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定
4. 在 中,已知 ,,,则 的面积为
A. B. C. D.
5. 年 月 日是全球首个国际圆周率日 .历史上,求圆周率 的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔 卡西的方法是:当正整数 充分大时,计算单位圆的内接正 边形的周长和外切正 边形(各边均与圆相切的正 边形)的周长,将它们的算术平均数作为 的近似值.按照阿尔 卡西的方法, 的近似值的表达式是
A. B.
C. D.
6. 已知在 中,角 ,, 的对边分别为 ,,,且 ,, 的面积为 ,则 等于
A. B. C. D.
7. 在 中,内角 ,, 所对应的边分别为 ,,,若 , , 则 的面积
A. B. C. D.
8. 在 中,若 ,则 的形状一定是
A. 等边三角形 B. 直角三角形
C. 等腰三角形 D. 等腰直角三角形
9. 在 中,角 ,, 的对边分别是 ,, 若 ,,则
A. B. C. D.
10. 已知锐角三角形的三边长分别为 ,,,那么 的取值范围为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 在 中,,,,则 的面积为 .
12. 在 中,,且 ,则此三角形为 .
13. 在钝角 中,内角 ,, 的对边分别为 ,, 若 ,,则最大边 的取值范围是 .
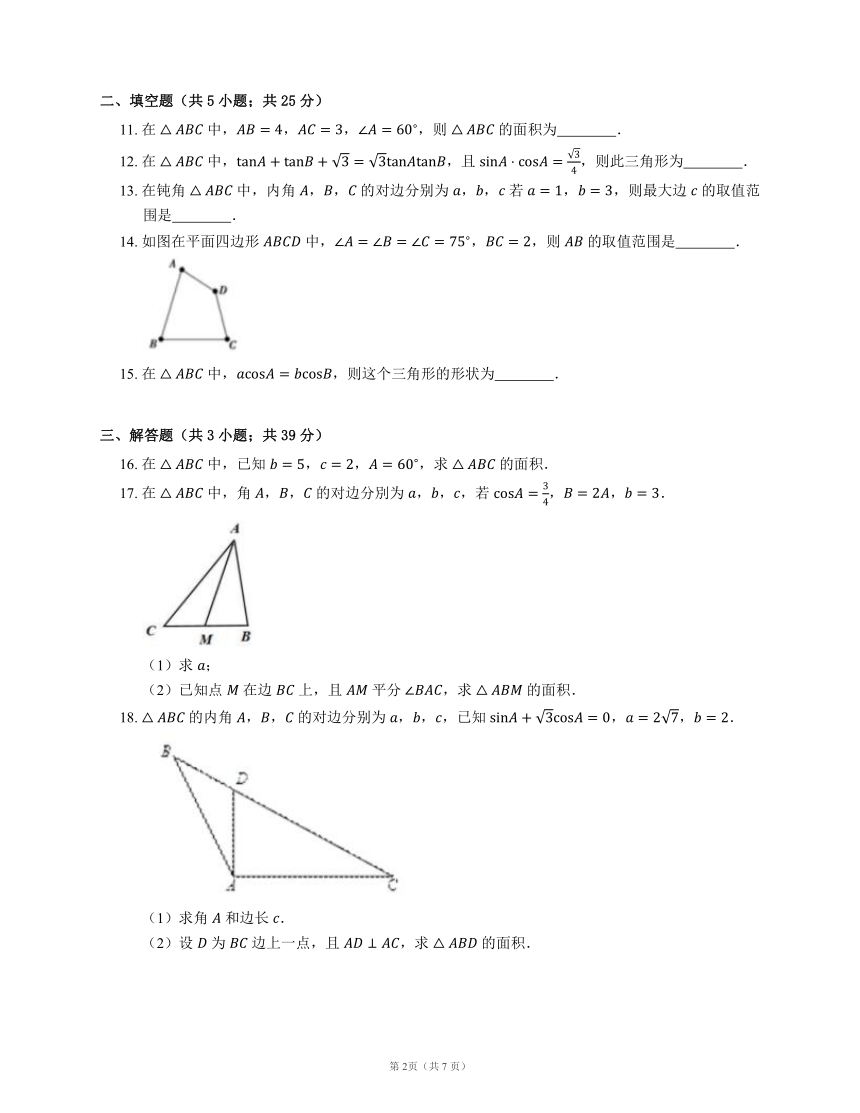
14. 如图在平面四边形 中,,,则 的取值范围是 .
15. 在 中,,则这个三角形的形状为 .
三、解答题(共3小题;共39分)
16. 在 中,已知 ,,,求 的面积.
17. 在 中,角 ,, 的对边分別为 ,,,若 ,,.
(1)求 ;
(2)已知点 在边 上,且 平分 ,求 的面积.
18. 的内角 ,, 的对边分别为 ,,,已知 ,,.
(1)求角 和边长 .
(2)设 为 边上一点,且 ,求 的面积.
答案
第一部分
1. B 【解析】由三角形的面积公式可得 .
2. C 【解析】由题可知 ,
所以 .
由余弦定理 ,
所以 .
因为 ,
所以 .
3. B 【解析】因为 ,
所以由正弦定理可得 ,
,
所以 ,,所以是直角三角形.
4. C 【解析】在 中,已知 ,,,
所以 .
5. A
【解析】设内接正 边形的周长为 ,
外切正 边形的周长为 ,如图()所示,
,
所以 ,
所以 ,.
如图()所示,
,
所以 ,
所以 ,.
所以 ,
所以 .
6. C 【解析】因为 ,
所以 .
由 ,可得 ,
根据余弦定理,得 ,
所以 .
7. C 【解析】因为 ,,
所以由余弦定理得:,
即 ,,
因此 的面积为 .
8. B
9. B 【解析】因为在 中 ,
所以由正弦定理可得 ,
又因为 ,
所以 ,
由 ①②可得 ,
可得 .
10. B
【解析】依题意 的三边长为 ,,,且 是锐角三角形.
当 为最大边长时,,设 所对的角为 ,根据余弦定理得 ,解得 .
当 为最大边长时,,设 所对的角为 ,根据余弦定理得 ,解得 .
综上所述,实数 的取值范围是 .
第二部分
11.
【解析】 的面积 .
12. 等边三角形
13.
【解析】因为 ,,
所以 ,即 ,
又 为钝角三角形,
所以 ,
所以根据余弦定理得,,
即 ,解得 ,
所以 ,
则最大边 的取值范围是 .
14.
【解析】如图所示,延长 , 交于 ,平移 ,
当 与 重合与 点时, 最长,
在 中,,,,
由正弦定理可得 ,
即 ,
解得 ,
平移 ,当 与 重合时, 最短,此时与 交于 ,
在 中,,,
由正弦定理知,,
即 ,
解得 ,
所以 的取值范围为 .
15. 等腰三角形或直角三角形
【解析】由正弦定理,得 ,
即 ,
所以 或 ,
即 或 ,
所以这个三角形为等腰三角形或直角三角形.
第三部分
16. .
17. (1) 因为 ,,,
所以 ,
由 得
(2) ,
所以 ,
所以 ,
由(),
由正弦定理得
又 平分 ,
所以 ,
又 ,
所以 ,,
所以
18. (1) 因为 ,
所以 ,
因为 ,
所以 ,
由余弦定理可得 ,
即 ,
即 ,
解得 (舍去)或 .
(2) 因为 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 在 中,角 ,, 所对的边分别为 ,,,若 ,,,则 的面积 等于
A. B. C. D.
2. 的内角 ,, 的对边分别为 ,,,若 的面积为 ,则
A. B. C. D.
3. 设在 中,角 ,, 所对的边分别为 ,,,若 ,则 的形状为
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定
4. 在 中,已知 ,,,则 的面积为
A. B. C. D.
5. 年 月 日是全球首个国际圆周率日 .历史上,求圆周率 的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔 卡西的方法是:当正整数 充分大时,计算单位圆的内接正 边形的周长和外切正 边形(各边均与圆相切的正 边形)的周长,将它们的算术平均数作为 的近似值.按照阿尔 卡西的方法, 的近似值的表达式是
A. B.
C. D.
6. 已知在 中,角 ,, 的对边分别为 ,,,且 ,, 的面积为 ,则 等于
A. B. C. D.
7. 在 中,内角 ,, 所对应的边分别为 ,,,若 , , 则 的面积
A. B. C. D.
8. 在 中,若 ,则 的形状一定是
A. 等边三角形 B. 直角三角形
C. 等腰三角形 D. 等腰直角三角形
9. 在 中,角 ,, 的对边分别是 ,, 若 ,,则
A. B. C. D.
10. 已知锐角三角形的三边长分别为 ,,,那么 的取值范围为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 在 中,,,,则 的面积为 .
12. 在 中,,且 ,则此三角形为 .
13. 在钝角 中,内角 ,, 的对边分别为 ,, 若 ,,则最大边 的取值范围是 .
14. 如图在平面四边形 中,,,则 的取值范围是 .
15. 在 中,,则这个三角形的形状为 .
三、解答题(共3小题;共39分)
16. 在 中,已知 ,,,求 的面积.
17. 在 中,角 ,, 的对边分別为 ,,,若 ,,.
(1)求 ;
(2)已知点 在边 上,且 平分 ,求 的面积.
18. 的内角 ,, 的对边分别为 ,,,已知 ,,.
(1)求角 和边长 .
(2)设 为 边上一点,且 ,求 的面积.
答案
第一部分
1. B 【解析】由三角形的面积公式可得 .
2. C 【解析】由题可知 ,
所以 .
由余弦定理 ,
所以 .
因为 ,
所以 .
3. B 【解析】因为 ,
所以由正弦定理可得 ,
,
所以 ,,所以是直角三角形.
4. C 【解析】在 中,已知 ,,,
所以 .
5. A
【解析】设内接正 边形的周长为 ,
外切正 边形的周长为 ,如图()所示,
,
所以 ,
所以 ,.
如图()所示,
,
所以 ,
所以 ,.
所以 ,
所以 .
6. C 【解析】因为 ,
所以 .
由 ,可得 ,
根据余弦定理,得 ,
所以 .
7. C 【解析】因为 ,,
所以由余弦定理得:,
即 ,,
因此 的面积为 .
8. B
9. B 【解析】因为在 中 ,
所以由正弦定理可得 ,
又因为 ,
所以 ,
由 ①②可得 ,
可得 .
10. B
【解析】依题意 的三边长为 ,,,且 是锐角三角形.
当 为最大边长时,,设 所对的角为 ,根据余弦定理得 ,解得 .
当 为最大边长时,,设 所对的角为 ,根据余弦定理得 ,解得 .
综上所述,实数 的取值范围是 .
第二部分
11.
【解析】 的面积 .
12. 等边三角形
13.
【解析】因为 ,,
所以 ,即 ,
又 为钝角三角形,
所以 ,
所以根据余弦定理得,,
即 ,解得 ,
所以 ,
则最大边 的取值范围是 .
14.
【解析】如图所示,延长 , 交于 ,平移 ,
当 与 重合与 点时, 最长,
在 中,,,,
由正弦定理可得 ,
即 ,
解得 ,
平移 ,当 与 重合时, 最短,此时与 交于 ,
在 中,,,
由正弦定理知,,
即 ,
解得 ,
所以 的取值范围为 .
15. 等腰三角形或直角三角形
【解析】由正弦定理,得 ,
即 ,
所以 或 ,
即 或 ,
所以这个三角形为等腰三角形或直角三角形.
第三部分
16. .
17. (1) 因为 ,,,
所以 ,
由 得
(2) ,
所以 ,
所以 ,
由(),
由正弦定理得
又 平分 ,
所以 ,
又 ,
所以 ,,
所以
18. (1) 因为 ,
所以 ,
因为 ,
所以 ,
由余弦定理可得 ,
即 ,
即 ,
解得 (舍去)或 .
(2) 因为 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 .
第1页(共1 页)
