2.6 求数列的通项公式(补充)(word含答案解析)
文档属性
| 名称 | 2.6 求数列的通项公式(补充)(word含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 17:01:21 | ||
图片预览



文档简介
2.6 求数列的通项公式(补充)
一、选择题(共10小题;共50分)
1. 数列 ,,,, 的通项公式 等于
A. B. C. D.
2. 已知数列 的前 项和 ,则
A. B. C. D.
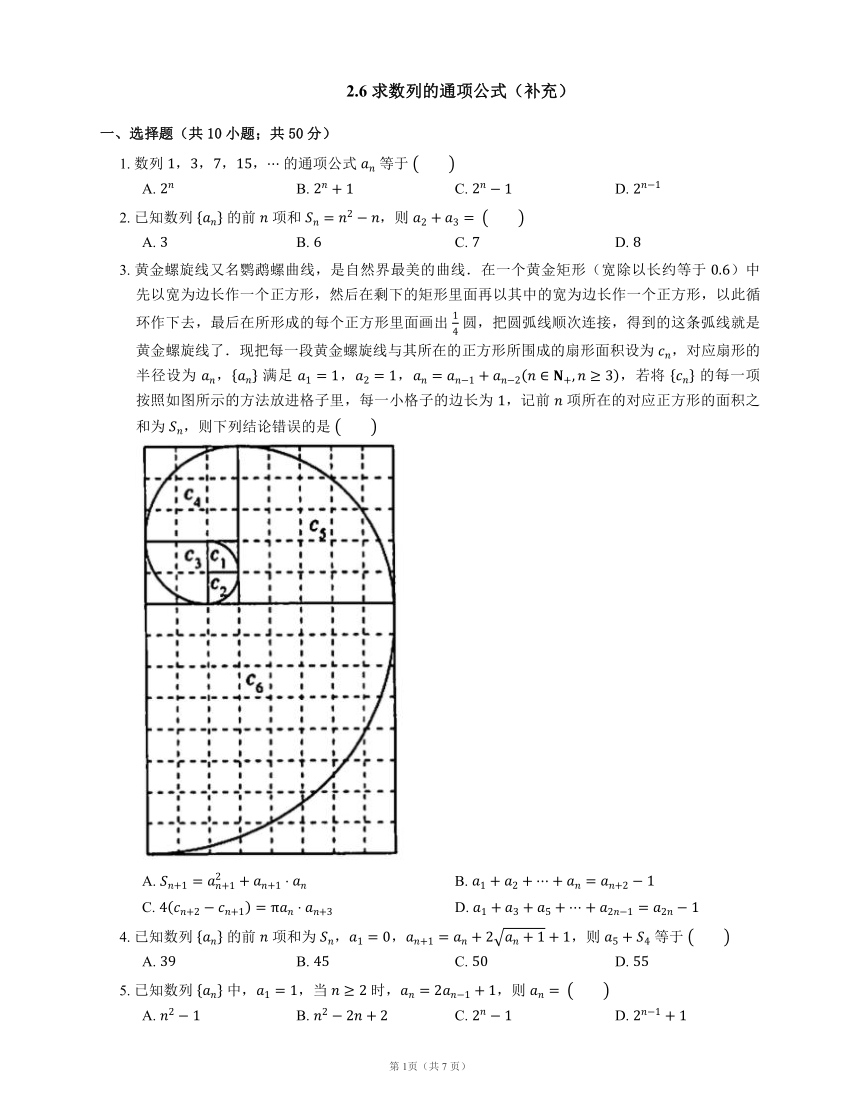
3. 黄金螺旋线又名鹦鹉螺曲线,是自然界最美的曲线.在一个黄金矩形(宽除以长约等于 )中先以宽为边长作一个正方形,然后在剩下的矩形里面再以其中的宽为边长作一个正方形,以此循环作下去,最后在所形成的每个正方形里面画出 圆,把圆弧线顺次连接,得到的这条弧线就是黄金螺旋线了.现把每一段黄金螺旋线与其所在的正方形所围成的扇形面积设为 ,对应扇形的半径设为 , 满足 ,,,若将 的每一项按照如图所示的方法放进格子里,每一小格子的边长为 ,记前 项所在的对应正方形的面积之和为 ,则下列结论错误的是
A. B.
C. D.
4. 已知数列 的前 项和为 ,,,则 等于
A. B. C. D.
5. 已知数列 中,,当 时,,则
A. B. C. D.
6. 大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.大衍数列是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是 ,,,,,,,,,,,则该数列的第 项为
A. B. C. D.
7. 在数列 中,已知 ,且对于任意的 ,都有 ,则数列 的通项公式为
A. B. C. D.
8. 已知数列 的前 项和为 ,且 ,则
A. B. C. D.
9. 在等差数列 中,,其前 项和为 ,若 ,则
A. B. C. D.
10. 在数列 中,,,则 的值为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 在数列 中,若 ,,则该数列的通项公式 .
12. 如图关于星星的图案构成一个数列,该数列的第 个图案有 .
13. 设数列 满足 ,其前 项和 ,,则 , .
14. 已知数列 满足 ,,则 .
15. 在数列 中,,,则 ,通项公式 .
三、解答题(共3小题;共39分)
16. 写出下列数列的一个通项公式.
(1),,,,;
(2),,,,;
(3),,,,;
17. 已知数列 满足 ,,求数列 的通项公式.
18. 设数列 的前 项和为 ,,已知 ,,,且当 时,.
(1)求 的值;
(2)证明: 为等比数列;
(3)求数列 的通项公式.
答案
第一部分
1. C
2. B
3. D 【解析】由题意得 是以 为宽, 为长的矩形的面积,
即 ,故A正确;
故B正确;
故C正确;
因为 ,
所以D错误.故选D.
4. C
5. C
【解析】答案:C
6. B 【解析】偶数项为 ,,,,,,
即 ,,,,,,记为 ,则偶数项对应的一个通项公式为 ,
原数列的第 项为第 个偶数,
故 ,即原数列的第 项为 .
7. D 【解析】令 ,得 ,
所以 ,
所以 ,,,,
所以 ,
所以 .
8. C 【解析】因为
所以当 时,
① ② 整理得 ,
令 ,得 .
9. C 【解析】设等差数列 的公差为 ,则 ,
所以 ,
所以数列 是首项为 ,公差为 的等差数列.
因为 ,
所以 ,
所以 ,
所以 .
10. B
第二部分
11.
【解析】在数列 中,因为 ,,所以 ,即 是以 为首项, 为公比的等比数列,所以 ,所以该数列的通项公式为 .
12.
【解析】观察数列中的星星构成的规律:
当 时,有 个,
当 时,有 个,
当 时,有 个,
所以当 时,有 个.
13. ,
【解析】因为 ,
所以 ,
① ②化简得 ,
所以 ,.
当 时,,解得 ,
所以当 时,.
又 不满足 , 满足 ,
所以 ,
所以 .
14.
【解析】依题意,由 ,
可得 ,
即 ,
因为 ,
所以数列 是以 为首项, 为差的等差数列,
所以 ,
所以 ,,
故 .
15. ,
【解析】由已知,.
因为 ,
所以 ,
,
,
所以以上 个式子累加可得,,
因为 ,所以 .
第三部分
16. (1) 这个数列前 项的分母都是序号乘比序号大 的数,并且奇数项为负,偶数项为正,所以它的一个通项公式为 ,.
(2) 这个数列的前 项的分母都是比序号大 的数,分子都是比序号大 的数的平方减 ,所以它的一个通项公式为 ,.
(3) 这个数列的前 项可以变形为 ,,,,
即 ,,,,
即 ,,,,
所以它的一个通项公式为 ,.
17. 两边同除以 ,得 ,,
则原式变为 ,设 ,
与原式待定系数,得 ,得 ,,,
所以数列 是一个公比为 的等比数列,首项为 ,
所以 ,,
所以 .
18. (1) 当 时,,即 ,
解得 .
(2) 由 ,得 ,即 .
,
,
.
数列 是以 为首项, 为公比的等比数列.
(3) 由(2)知,,
即 .
数列 是以 为首项, 为公差的等差数列,
,
即 ,
数列 的通项公式为 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 数列 ,,,, 的通项公式 等于
A. B. C. D.
2. 已知数列 的前 项和 ,则
A. B. C. D.
3. 黄金螺旋线又名鹦鹉螺曲线,是自然界最美的曲线.在一个黄金矩形(宽除以长约等于 )中先以宽为边长作一个正方形,然后在剩下的矩形里面再以其中的宽为边长作一个正方形,以此循环作下去,最后在所形成的每个正方形里面画出 圆,把圆弧线顺次连接,得到的这条弧线就是黄金螺旋线了.现把每一段黄金螺旋线与其所在的正方形所围成的扇形面积设为 ,对应扇形的半径设为 , 满足 ,,,若将 的每一项按照如图所示的方法放进格子里,每一小格子的边长为 ,记前 项所在的对应正方形的面积之和为 ,则下列结论错误的是
A. B.
C. D.
4. 已知数列 的前 项和为 ,,,则 等于
A. B. C. D.
5. 已知数列 中,,当 时,,则
A. B. C. D.
6. 大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.大衍数列是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是 ,,,,,,,,,,,则该数列的第 项为
A. B. C. D.
7. 在数列 中,已知 ,且对于任意的 ,都有 ,则数列 的通项公式为
A. B. C. D.
8. 已知数列 的前 项和为 ,且 ,则
A. B. C. D.
9. 在等差数列 中,,其前 项和为 ,若 ,则
A. B. C. D.
10. 在数列 中,,,则 的值为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 在数列 中,若 ,,则该数列的通项公式 .
12. 如图关于星星的图案构成一个数列,该数列的第 个图案有 .
13. 设数列 满足 ,其前 项和 ,,则 , .
14. 已知数列 满足 ,,则 .
15. 在数列 中,,,则 ,通项公式 .
三、解答题(共3小题;共39分)
16. 写出下列数列的一个通项公式.
(1),,,,;
(2),,,,;
(3),,,,;
17. 已知数列 满足 ,,求数列 的通项公式.
18. 设数列 的前 项和为 ,,已知 ,,,且当 时,.
(1)求 的值;
(2)证明: 为等比数列;
(3)求数列 的通项公式.
答案
第一部分
1. C
2. B
3. D 【解析】由题意得 是以 为宽, 为长的矩形的面积,
即 ,故A正确;
故B正确;
故C正确;
因为 ,
所以D错误.故选D.
4. C
5. C
【解析】答案:C
6. B 【解析】偶数项为 ,,,,,,
即 ,,,,,,记为 ,则偶数项对应的一个通项公式为 ,
原数列的第 项为第 个偶数,
故 ,即原数列的第 项为 .
7. D 【解析】令 ,得 ,
所以 ,
所以 ,,,,
所以 ,
所以 .
8. C 【解析】因为
所以当 时,
① ② 整理得 ,
令 ,得 .
9. C 【解析】设等差数列 的公差为 ,则 ,
所以 ,
所以数列 是首项为 ,公差为 的等差数列.
因为 ,
所以 ,
所以 ,
所以 .
10. B
第二部分
11.
【解析】在数列 中,因为 ,,所以 ,即 是以 为首项, 为公比的等比数列,所以 ,所以该数列的通项公式为 .
12.
【解析】观察数列中的星星构成的规律:
当 时,有 个,
当 时,有 个,
当 时,有 个,
所以当 时,有 个.
13. ,
【解析】因为 ,
所以 ,
① ②化简得 ,
所以 ,.
当 时,,解得 ,
所以当 时,.
又 不满足 , 满足 ,
所以 ,
所以 .
14.
【解析】依题意,由 ,
可得 ,
即 ,
因为 ,
所以数列 是以 为首项, 为差的等差数列,
所以 ,
所以 ,,
故 .
15. ,
【解析】由已知,.
因为 ,
所以 ,
,
,
所以以上 个式子累加可得,,
因为 ,所以 .
第三部分
16. (1) 这个数列前 项的分母都是序号乘比序号大 的数,并且奇数项为负,偶数项为正,所以它的一个通项公式为 ,.
(2) 这个数列的前 项的分母都是比序号大 的数,分子都是比序号大 的数的平方减 ,所以它的一个通项公式为 ,.
(3) 这个数列的前 项可以变形为 ,,,,
即 ,,,,
即 ,,,,
所以它的一个通项公式为 ,.
17. 两边同除以 ,得 ,,
则原式变为 ,设 ,
与原式待定系数,得 ,得 ,,,
所以数列 是一个公比为 的等比数列,首项为 ,
所以 ,,
所以 .
18. (1) 当 时,,即 ,
解得 .
(2) 由 ,得 ,即 .
,
,
.
数列 是以 为首项, 为公比的等比数列.
(3) 由(2)知,,
即 .
数列 是以 为首项, 为公差的等差数列,
,
即 ,
数列 的通项公式为 .
第1页(共1 页)
