3.3 二元一次不等式(组)与简单的线性规划问题(word含答案解析)
文档属性
| 名称 | 3.3 二元一次不等式(组)与简单的线性规划问题(word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 00:00:00 | ||
图片预览



文档简介
3.3 二元一次不等式(组)与简单的线性规划问题
一、选择题(共10小题;共50分)
1. 不等式组 表示的平面区域是一个
A. 三角形 B. 直角梯形 C. 等腰梯形 D. 矩形
2. 已知实数 , 满足约束条件 则 的最大值为
A. B. C. D.
3. 设实数 , 满足 则 的最大值是
A. B. C. D.
4. 在坐标平面上,不等式 所表示的平面区域的面积为
A. B. C. D.
5. 不等式组 所表示的平面区域的面积为
A. B. C. D.
6. 不在 表示的平面区域内的一个点是
A. B. C. D.
7. 已知 ,.若点 在线段 上,则 的最大值为
A. B. C. D.
8. 众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.下图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在 轴右侧部分的边界为一个半圆,已知直线 :.给出以下命题:
①当 时,若直线 截黑色阴影区域所得两部分面积记为 ,,则 ;
②当 时,直线 与黑色阴影区域有 个公共点;
③当 时,直线 与黑色阴影区域有 个公共点.
其中所有正确命题的序号是
A. ①② B. ①③ C. ②③ D. ①②③
9. 已知实数 , 满足约束条件 则 的最大值等于
A. B. C. D.
10. 若实数 ,,满足 则 的最小值为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 由直线 , 和 围成的三角形(包括边界)用不等式组可表示为 .
12. 已知 的三边长 ,, 满足 ,,则 的取值范围是 .
13. 若不等式组 表示的平面区域是一个四边形,则实数 的取值范围是 .
14. 已知实数 , 满足约束条件 则 的最大值为 , 的最小值为 .
15. 由不等式组 表示的平面区域内的整点(横、纵坐标都是整数的点)个数为 .
三、解答题(共3小题;共39分)
16. 如图所示,写出阴影区域(包含直线)所对应的二元一次不等式组.
17. 求满足下列约束条件的目标函数 的最小值:
18. 若实系数方程 的两实根分别在区间 与 内,求 的取值范围.
答案
第一部分
1. C
2. C
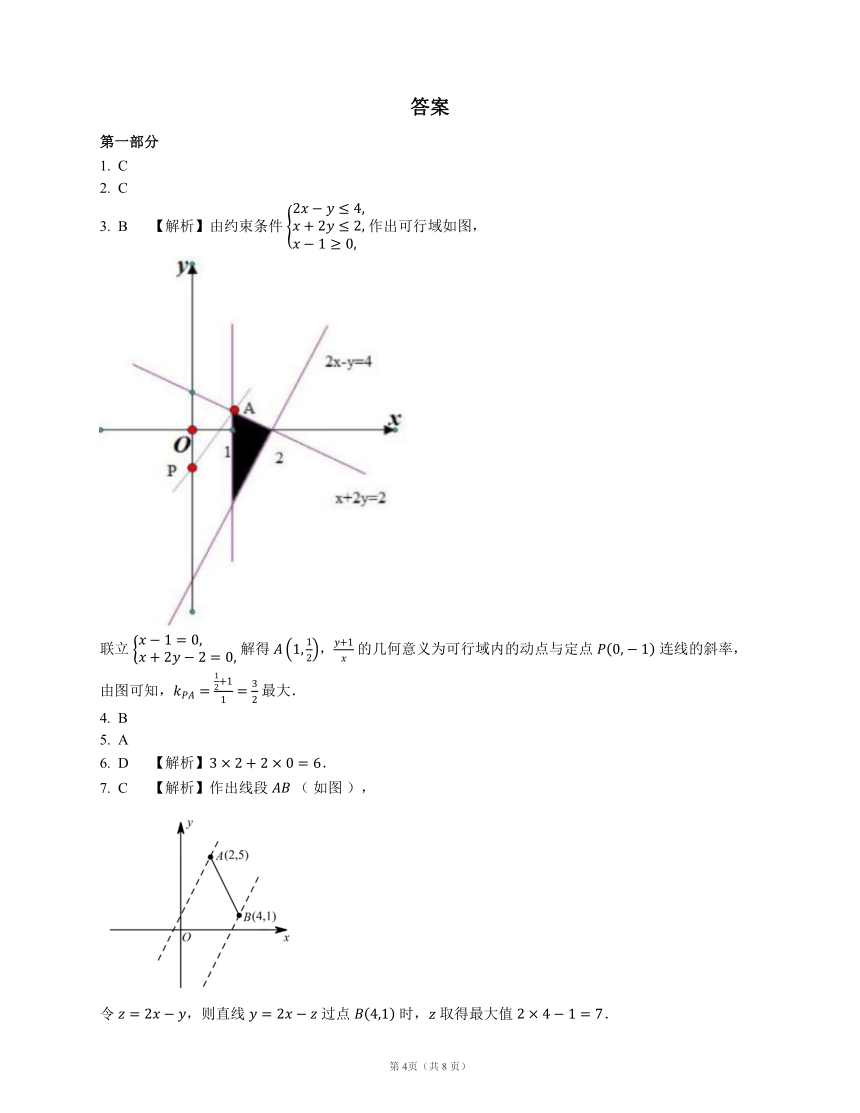
3. B 【解析】由约束条件 作出可行域如图,
联立 解得 , 的几何意义为可行域内的动点与定点 连线的斜率,由图可知, 最大.
4. B
5. A
6. D 【解析】.
7. C 【解析】作出线段 ( 如图 ),
令 ,则直线 过点 时, 取得最大值 .
8. A 【解析】对于①,当 时,,,,,①正确;对于②, 时,点 到直线 的距离为 ,故直线与右侧黑半圆相切,②正确;对于③,直线过定点 ,,直线 与黑色阴影区域有无数个公共点,③错误.
9. D 【解析】由约束条件作出可行域如图,
联立 解得 ,
由 ,得 ,
由图可知,当直线 过 时,直线在 轴上的截距最大, 有最大值为 .
故选:D.
10. D
第二部分
11.
【解析】画出三条直线,并用阴影表示三角形区域,如图所示.
将 , 代入 ,得 ;
将 , 代入 ,得 ;
将 , 代入 ,得 .
结合图形可知,三角形区域用不等式组可表示为
12.
【解析】因为 ,,且 ,,
所以不等式组 有解,
所以
所以 ,即 的取值范围是 .
13.
14. ,
【解析】作出可行域如图中阴影部分所示(包含边界),
令 ,则 ,
由图可知,当直线 过点 时, 取得最大值,.
的几何意义是可行域内的点与原点的距离的平方,
由图可知 的最小值为原点 到直线 的距离的平方,
故 的最小值为 .
15.
【解析】不等式组 表示的平面区域如下图所示:
由图可知,整数点有:
时,有 个;
时,有 个;
时,有 个;
时,有 个;
时,有 个;
共有:.
第三部分
16.
17. 阴影部分区域的顶点坐标分别为 ,,,所以目标函数 在点 处取得最小值 .
18. 由题意,得
目标函数 为满足条件的 与 的连线的斜率.
画出可行域可得,当 时,;
当 时,,
所以 的取值范围为 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 不等式组 表示的平面区域是一个
A. 三角形 B. 直角梯形 C. 等腰梯形 D. 矩形
2. 已知实数 , 满足约束条件 则 的最大值为
A. B. C. D.
3. 设实数 , 满足 则 的最大值是
A. B. C. D.
4. 在坐标平面上,不等式 所表示的平面区域的面积为
A. B. C. D.
5. 不等式组 所表示的平面区域的面积为
A. B. C. D.
6. 不在 表示的平面区域内的一个点是
A. B. C. D.
7. 已知 ,.若点 在线段 上,则 的最大值为
A. B. C. D.
8. 众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.下图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在 轴右侧部分的边界为一个半圆,已知直线 :.给出以下命题:
①当 时,若直线 截黑色阴影区域所得两部分面积记为 ,,则 ;
②当 时,直线 与黑色阴影区域有 个公共点;
③当 时,直线 与黑色阴影区域有 个公共点.
其中所有正确命题的序号是
A. ①② B. ①③ C. ②③ D. ①②③
9. 已知实数 , 满足约束条件 则 的最大值等于
A. B. C. D.
10. 若实数 ,,满足 则 的最小值为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 由直线 , 和 围成的三角形(包括边界)用不等式组可表示为 .
12. 已知 的三边长 ,, 满足 ,,则 的取值范围是 .
13. 若不等式组 表示的平面区域是一个四边形,则实数 的取值范围是 .
14. 已知实数 , 满足约束条件 则 的最大值为 , 的最小值为 .
15. 由不等式组 表示的平面区域内的整点(横、纵坐标都是整数的点)个数为 .
三、解答题(共3小题;共39分)
16. 如图所示,写出阴影区域(包含直线)所对应的二元一次不等式组.
17. 求满足下列约束条件的目标函数 的最小值:
18. 若实系数方程 的两实根分别在区间 与 内,求 的取值范围.
答案
第一部分
1. C
2. C
3. B 【解析】由约束条件 作出可行域如图,
联立 解得 , 的几何意义为可行域内的动点与定点 连线的斜率,由图可知, 最大.
4. B
5. A
6. D 【解析】.
7. C 【解析】作出线段 ( 如图 ),
令 ,则直线 过点 时, 取得最大值 .
8. A 【解析】对于①,当 时,,,,,①正确;对于②, 时,点 到直线 的距离为 ,故直线与右侧黑半圆相切,②正确;对于③,直线过定点 ,,直线 与黑色阴影区域有无数个公共点,③错误.
9. D 【解析】由约束条件作出可行域如图,
联立 解得 ,
由 ,得 ,
由图可知,当直线 过 时,直线在 轴上的截距最大, 有最大值为 .
故选:D.
10. D
第二部分
11.
【解析】画出三条直线,并用阴影表示三角形区域,如图所示.
将 , 代入 ,得 ;
将 , 代入 ,得 ;
将 , 代入 ,得 .
结合图形可知,三角形区域用不等式组可表示为
12.
【解析】因为 ,,且 ,,
所以不等式组 有解,
所以
所以 ,即 的取值范围是 .
13.
14. ,
【解析】作出可行域如图中阴影部分所示(包含边界),
令 ,则 ,
由图可知,当直线 过点 时, 取得最大值,.
的几何意义是可行域内的点与原点的距离的平方,
由图可知 的最小值为原点 到直线 的距离的平方,
故 的最小值为 .
15.
【解析】不等式组 表示的平面区域如下图所示:
由图可知,整数点有:
时,有 个;
时,有 个;
时,有 个;
时,有 个;
时,有 个;
共有:.
第三部分
16.
17. 阴影部分区域的顶点坐标分别为 ,,,所以目标函数 在点 处取得最小值 .
18. 由题意,得
目标函数 为满足条件的 与 的连线的斜率.
画出可行域可得,当 时,;
当 时,,
所以 的取值范围为 .
第1页(共1 页)
