3.3垂径定理 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析)
文档属性
| 名称 | 3.3垂径定理 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 11:45:15 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.3垂径定理》
期末复习自主提升训练(附答案)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
2.如图,在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6 B.9 C.12 D.15
3.如图,在⊙O中,点A,B在圆上,∠AOB=120°,弦AB的长度为4√3,则半径OA的长度为( )
A.2 B.4 C.2 D.3
4.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
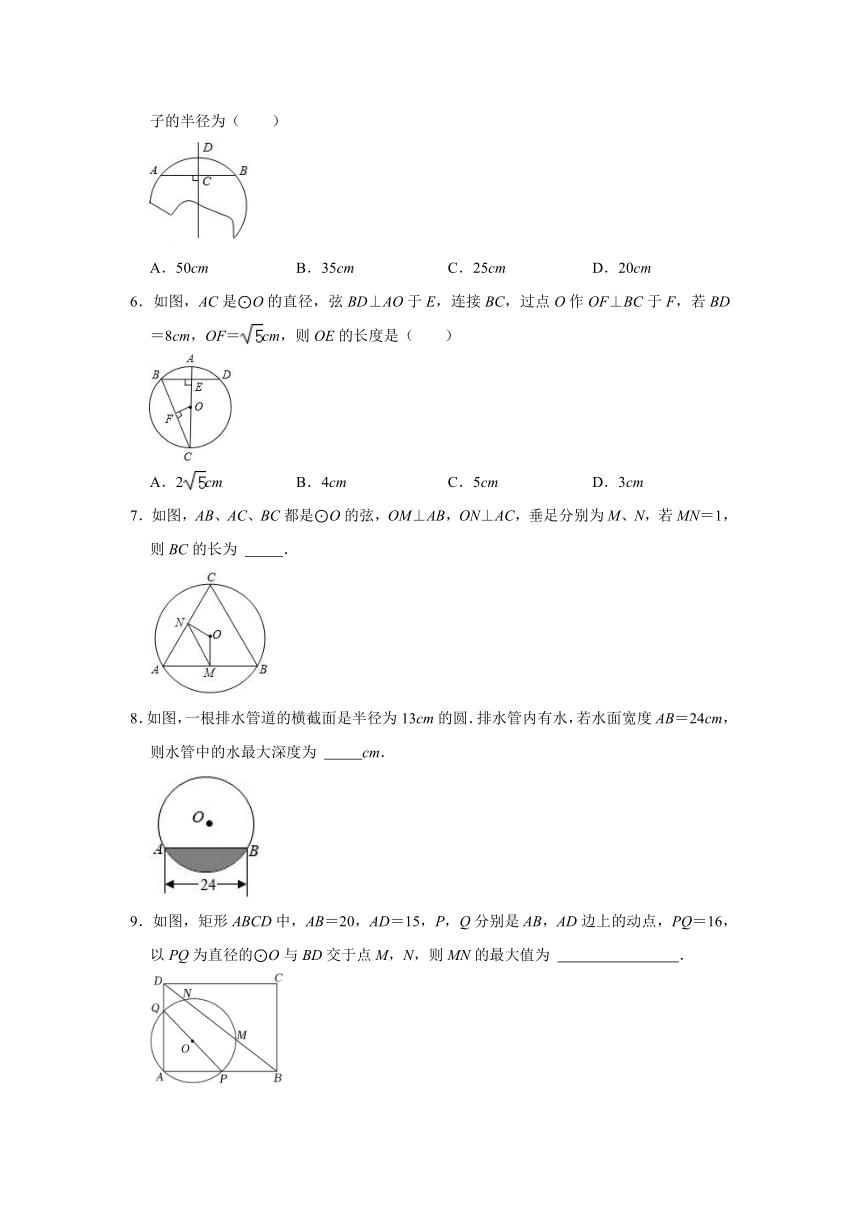
5.数学活动课上,同学们想测出一个残损轮子的半径,小的解决方案如下:如图,在轮子圆弧上任取两点A,B,连接AB,再作出AB的垂直平分线,交AB于点C,交于点D,测出AB,CD的长度,即可计算得出轮子的半径.现测出AB=40cm,CD=10cm,则轮子的半径为( )
A.50cm B.35cm C.25cm D.20cm
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,OF=cm,则OE的长度是( )
A.2cm B.4cm C.5cm D.3cm
7.如图,AB、AC、BC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,若MN=1,则BC的长为 .
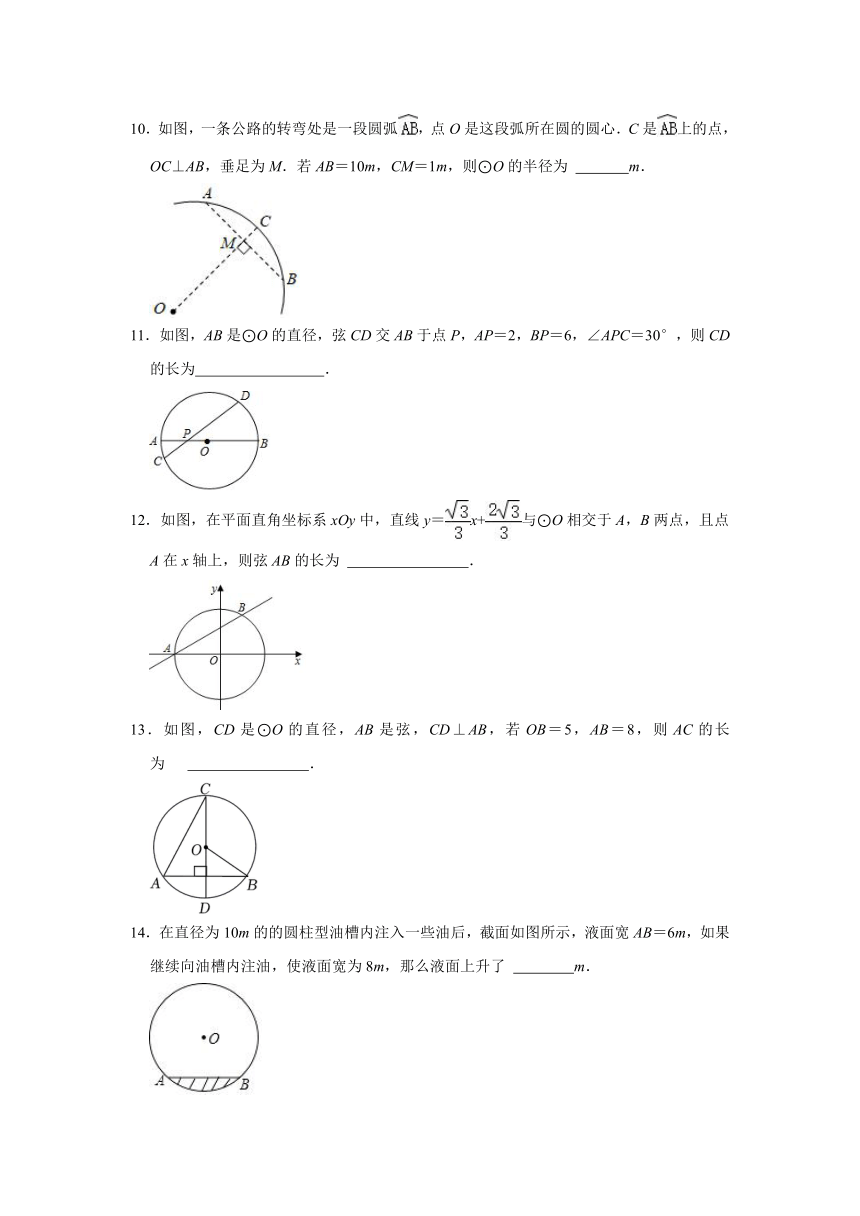
8.如图,一根排水管道的横截面是半径为13cm的圆.排水管内有水,若水面宽度AB=24cm,则水管中的水最大深度为 cm.
9.如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .
10.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心.C是上的点,OC⊥AB,垂足为M.若AB=10m,CM=1m,则⊙O的半径为 m.
11.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 .
12.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
13.如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 .
14.在直径为10m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了 m.
15.如图,AB是圆O的直径,AC是弦,半径OD垂直AC于E,连接BE,过O作BE的垂线,垂足是F,如果AC=8,DE=2.
(1)求BE的长;
(2)求OF的长.
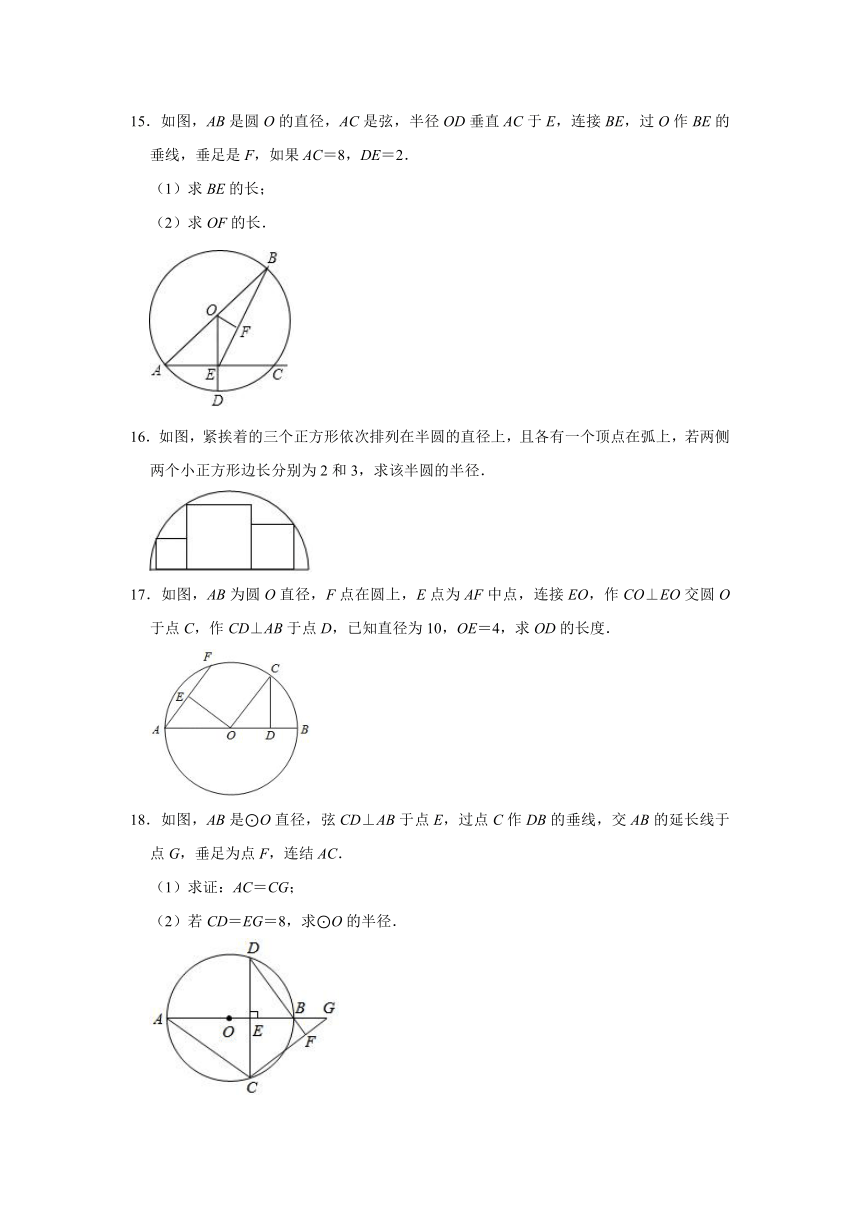
16.如图,紧挨着的三个正方形依次排列在半圆的直径上,且各有一个顶点在弧上,若两侧两个小正方形边长分别为2和3,求该半圆的半径.
17.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
18.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
19.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
20.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
参考答案
1.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
2.解:∵直径AB=15,
∴OD=OB=,
∵OC:OB=3:5,
∴OC=,
∵DE⊥AB,
∴CD=CE,
在Rt△OCD中,由勾股定理得:CD===6,
∴DE=2CD=12,
故选:C.
3.解:过O作OC⊥AB于C,
则AC=BC=AB,∠ACO=∠BCO=90°,
∵弦AB的长度为4,
∴AC=BC=2,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OC=OA,
∵OA2=OC2+AC2,
∴OA2=(OA)2+(2)2,
解得OA=4,
故选:B.
4.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
5.解:设圆心为O,连接OB.
Rt△OBC中,BC=AB=20cm,
根据勾股定理得:
OC2+BC2=OB2,即:
(OB﹣10)2+202=OB2,
解得:OB=25;
故轮子的半径为25cm.
故选:C.
6.解:连接OB、AB,
∵BD⊥AO,BD=8cm,
∴BE=ED=BD=4(cm),
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=cm,
∴AB=2OF=2(cm),
由勾股定理得:AE==2(cm),
在Rt△BOE中,OB2=OE2+BE2,即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3(cm),
故选:D.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,OM过圆心O,ON过圆心O,
∴AN=CN,AM=BM,
∴MN=BC,
∵MN=1,
∴BC=2,
故答案为:2.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水管中的水最大深度为8cm,
故答案为:8.
9.解:过A点作AH⊥BD于H,连接OM,如图:
∵四边形ABCD是矩形,
∴∠BAD=90°,
在Rt△ABD中,BD===25,
∵×AH×BD=×AD×AB,
∴AH==12,
∵⊙O的直径为16,
∴⊙O的半径为8,
∴点O在AH上时,OH最短,
∵HM=,
∴此时HM有最大值,OH=AH﹣OA=4,
则最大值为=4,
∵OH⊥MN,
∴MN=2MH,
∴MN的最大值为2×4=8.故答案为:8.
10.解:连接OA,如图所示:
设⊙O的半径为rm,
∵OC⊥AB,AB=10m,
∴AM=BM=AB=5(m),
在Rt△AOD中,由勾股定理得:OA2=OM2+AM2,
即:r2=(r﹣1)2+52,
解得:r=13,
即⊙O的半径为13m.
故答案为:13.
11.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
12.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,故答案为:2.
13.解:如图,
∵CD⊥AB,AB=8,
∴AE=BE=4,
由勾股定理得:OE===3,
∴CE=OC+OE=5+3=8,
由勾股定理得:AC===4.
故答案为:4.
14.解:连接OA,作OG⊥AB于G,
∵AB=6m,
∴AG=AB=3m,
∵油槽直径为10m.
∴OA=5m,
∴OG=4m,即弦AB的弦心距是4m,
同理当油面宽AB为8m时,弦心距是3m,
∴当油面没超过圆心O时,油上升了1m;
当油面超过圆心O时,油上升了7m.
故答案为1或7.
15.解:(1)连接BC,
设圆O的半径为r,则OE=OD﹣DE=r﹣2,
∵OD⊥AC,AC=8,
∴AE=CE=AC=4,
在Rt△AOE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
∴OE=3,
∵OA=OB,AE=CE,
∴OE是△ABC的中位线,
∴BC=2OE=6,
∵AB是圆O的直径,
∴∠ACB=90°,
∴BE===2;
(2)由(1)得:∠ACB=90°,AE=CE,
∴S△ABE=S△ABC=××8×6=12,
又∵S△OBE=BE×OF=S△ABE﹣S△OAE=12﹣×4×3=6,
∴OF==.
16.解:如图,延长DF交⊙O于M,连接CO,DN,EN,MN,DO.
∵AB⊥DM,
∴DF=FM,
∵DF=FN,
∴FD=FN=FM,
∴∠DNM=90°,
∴∠DNF=∠FNM=∠M=45°,
∵∠ENK=45°,
∴E、N、M共线,
∴∠DOE=2∠DME=90°,
∵∠DOF+∠ODF=90°,∠DOF+∠EOK=90°,
∴∠ODF=∠EOK,
在△DOF和△EOK中,
,
∴△DOF≌△EOK(AAS),
∴OF=EK=3,
∴OA=2+3=5,
在Rt△AOC中,CO===;
故该半圆的半径为.
17.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
18.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
19.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
20.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
期末复习自主提升训练(附答案)
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
2.如图,在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6 B.9 C.12 D.15
3.如图,在⊙O中,点A,B在圆上,∠AOB=120°,弦AB的长度为4√3,则半径OA的长度为( )
A.2 B.4 C.2 D.3
4.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
5.数学活动课上,同学们想测出一个残损轮子的半径,小的解决方案如下:如图,在轮子圆弧上任取两点A,B,连接AB,再作出AB的垂直平分线,交AB于点C,交于点D,测出AB,CD的长度,即可计算得出轮子的半径.现测出AB=40cm,CD=10cm,则轮子的半径为( )
A.50cm B.35cm C.25cm D.20cm
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,OF=cm,则OE的长度是( )
A.2cm B.4cm C.5cm D.3cm
7.如图,AB、AC、BC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,若MN=1,则BC的长为 .
8.如图,一根排水管道的横截面是半径为13cm的圆.排水管内有水,若水面宽度AB=24cm,则水管中的水最大深度为 cm.
9.如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .
10.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心.C是上的点,OC⊥AB,垂足为M.若AB=10m,CM=1m,则⊙O的半径为 m.
11.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 .
12.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
13.如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 .
14.在直径为10m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了 m.
15.如图,AB是圆O的直径,AC是弦,半径OD垂直AC于E,连接BE,过O作BE的垂线,垂足是F,如果AC=8,DE=2.
(1)求BE的长;
(2)求OF的长.
16.如图,紧挨着的三个正方形依次排列在半圆的直径上,且各有一个顶点在弧上,若两侧两个小正方形边长分别为2和3,求该半圆的半径.
17.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
18.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
19.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
20.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
参考答案
1.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
2.解:∵直径AB=15,
∴OD=OB=,
∵OC:OB=3:5,
∴OC=,
∵DE⊥AB,
∴CD=CE,
在Rt△OCD中,由勾股定理得:CD===6,
∴DE=2CD=12,
故选:C.
3.解:过O作OC⊥AB于C,
则AC=BC=AB,∠ACO=∠BCO=90°,
∵弦AB的长度为4,
∴AC=BC=2,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OC=OA,
∵OA2=OC2+AC2,
∴OA2=(OA)2+(2)2,
解得OA=4,
故选:B.
4.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
5.解:设圆心为O,连接OB.
Rt△OBC中,BC=AB=20cm,
根据勾股定理得:
OC2+BC2=OB2,即:
(OB﹣10)2+202=OB2,
解得:OB=25;
故轮子的半径为25cm.
故选:C.
6.解:连接OB、AB,
∵BD⊥AO,BD=8cm,
∴BE=ED=BD=4(cm),
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=cm,
∴AB=2OF=2(cm),
由勾股定理得:AE==2(cm),
在Rt△BOE中,OB2=OE2+BE2,即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3(cm),
故选:D.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,OM过圆心O,ON过圆心O,
∴AN=CN,AM=BM,
∴MN=BC,
∵MN=1,
∴BC=2,
故答案为:2.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水管中的水最大深度为8cm,
故答案为:8.
9.解:过A点作AH⊥BD于H,连接OM,如图:
∵四边形ABCD是矩形,
∴∠BAD=90°,
在Rt△ABD中,BD===25,
∵×AH×BD=×AD×AB,
∴AH==12,
∵⊙O的直径为16,
∴⊙O的半径为8,
∴点O在AH上时,OH最短,
∵HM=,
∴此时HM有最大值,OH=AH﹣OA=4,
则最大值为=4,
∵OH⊥MN,
∴MN=2MH,
∴MN的最大值为2×4=8.故答案为:8.
10.解:连接OA,如图所示:
设⊙O的半径为rm,
∵OC⊥AB,AB=10m,
∴AM=BM=AB=5(m),
在Rt△AOD中,由勾股定理得:OA2=OM2+AM2,
即:r2=(r﹣1)2+52,
解得:r=13,
即⊙O的半径为13m.
故答案为:13.
11.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
12.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,故答案为:2.
13.解:如图,
∵CD⊥AB,AB=8,
∴AE=BE=4,
由勾股定理得:OE===3,
∴CE=OC+OE=5+3=8,
由勾股定理得:AC===4.
故答案为:4.
14.解:连接OA,作OG⊥AB于G,
∵AB=6m,
∴AG=AB=3m,
∵油槽直径为10m.
∴OA=5m,
∴OG=4m,即弦AB的弦心距是4m,
同理当油面宽AB为8m时,弦心距是3m,
∴当油面没超过圆心O时,油上升了1m;
当油面超过圆心O时,油上升了7m.
故答案为1或7.
15.解:(1)连接BC,
设圆O的半径为r,则OE=OD﹣DE=r﹣2,
∵OD⊥AC,AC=8,
∴AE=CE=AC=4,
在Rt△AOE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
∴OE=3,
∵OA=OB,AE=CE,
∴OE是△ABC的中位线,
∴BC=2OE=6,
∵AB是圆O的直径,
∴∠ACB=90°,
∴BE===2;
(2)由(1)得:∠ACB=90°,AE=CE,
∴S△ABE=S△ABC=××8×6=12,
又∵S△OBE=BE×OF=S△ABE﹣S△OAE=12﹣×4×3=6,
∴OF==.
16.解:如图,延长DF交⊙O于M,连接CO,DN,EN,MN,DO.
∵AB⊥DM,
∴DF=FM,
∵DF=FN,
∴FD=FN=FM,
∴∠DNM=90°,
∴∠DNF=∠FNM=∠M=45°,
∵∠ENK=45°,
∴E、N、M共线,
∴∠DOE=2∠DME=90°,
∵∠DOF+∠ODF=90°,∠DOF+∠EOK=90°,
∴∠ODF=∠EOK,
在△DOF和△EOK中,
,
∴△DOF≌△EOK(AAS),
∴OF=EK=3,
∴OA=2+3=5,
在Rt△AOC中,CO===;
故该半圆的半径为.
17.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
18.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
19.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
20.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
