3.5确定圆的条件 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析)
文档属性
| 名称 | 3.5确定圆的条件 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 11:50:13 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3.5确定圆的条件》
期末复习自主提升训练(附答案)
1.已知⊙O的半径为5cm,P到圆心O的距离为6cm,则点P与⊙O的位置关系是( )
A.点P在圆外 B.点P在圆上 C.点P在圆内 D.不能确定
2.已知OA=4,以O为圆心,r为半径作⊙O.若使点A在⊙O内,则r的值可以是( )
A.2 B.3 C.4 D.5
3.如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
A.4 B.2 C.3 D.
4.如图,⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=AC=5,则BC长为( )
A.10 B.9 C.8 D.5
5.如图,△ABC内接于⊙O,其外角∠BAE的平分线交⊙O于点D,点A为弧CD的中点.若∠ABC=28°,则∠ACB的大小为( )
A.84° B.85° C.86° D.88°
6.若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
7.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
9.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.过任意三点可以画一个圆
C.周长相等的圆是等圆 D.平分弦的直径垂直于弦
10.平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
11.如图所示,⊙O是△ABC的外接圆,已知∠ABO=25°,则∠ACB的大小为( )
A.50° B.55° C.65° D.75°
12.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
13.如图,△ABC内接于⊙O,∠A=40°,E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的度数是 .
14.如图AB=AC,∠A=40°,O是△ABC外接圆圆心,BO交AC于点D,则∠BDC= .
15.如图,△ABC是⊙O的内接三角形,AD是△ABC的高,AE是⊙O的直径,且AE=4,若CD=1,AC=3,则AB的长为 .
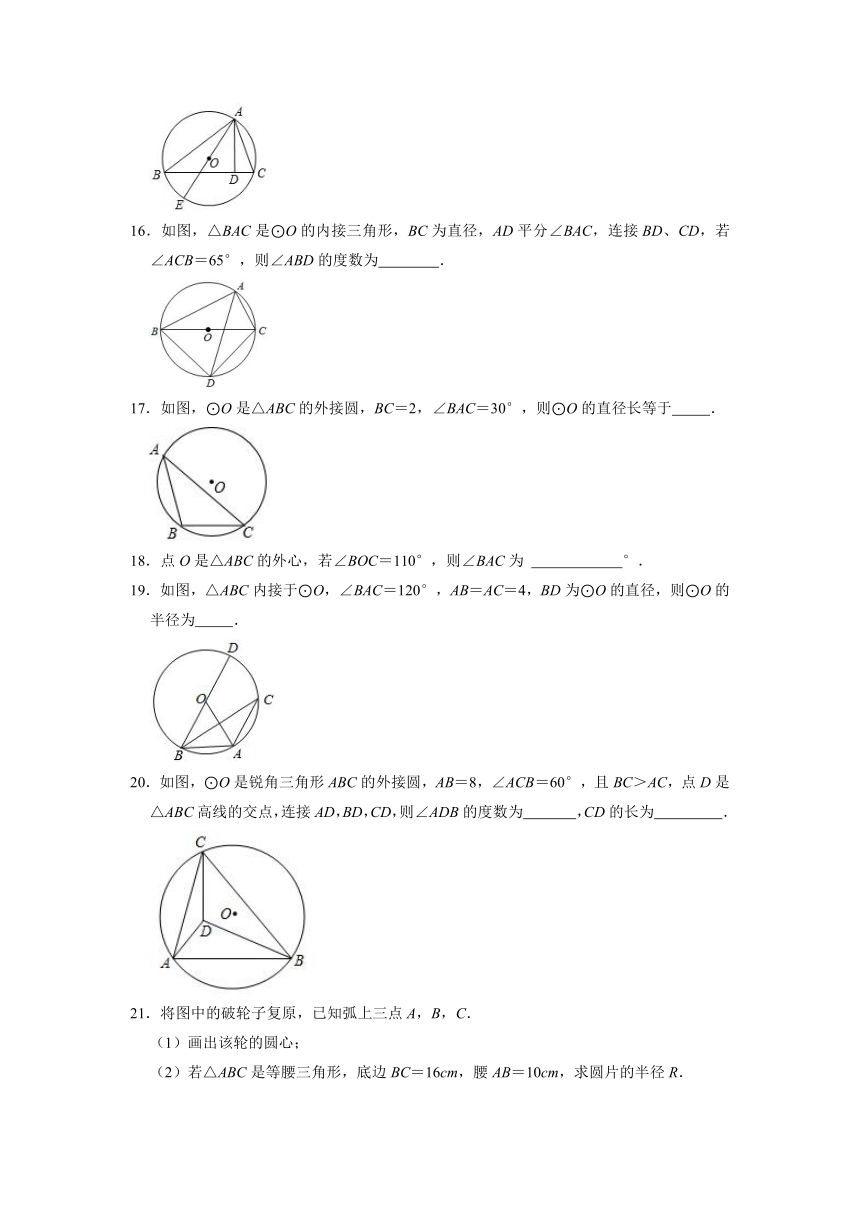
16.如图,△BAC是⊙O的内接三角形,BC为直径,AD平分∠BAC,连接BD、CD,若∠ACB=65°,则∠ABD的度数为 .
17.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则⊙O的直径长等于 .
18.点O是△ABC的外心,若∠BOC=110°,则∠BAC为 °.
19.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为 .
20.如图,⊙O是锐角三角形ABC的外接圆,AB=8,∠ACB=60°,且BC>AC,点D是△ABC高线的交点,连接AD,BD,CD,则∠ADB的度数为 ,CD的长为 .
21.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
22.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
23.如图,已知⊙O是△ABC的外接圆,直径AD与BC垂直,垂足为点E.
(1)求证:∠ABC=∠ACB;
(2)连接OB,CD,若OB=,CD=5,求CE的长.
24.如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
25.△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
参考答案
1.解:∵⊙O的半径为5cm,点P到圆心O的距离为6cm,
∴OP>⊙O的半径,
∴点P在⊙O外.
故选:A.
2.解:∵已知OA=4,以O为圆心,r为半径作⊙O.若使点A在⊙O内,
∴点A到圆心的距离应该小于圆的半径,
∴圆的半径应该大于4.
故选:D.
3.解:过点O作OM⊥BC,交BC于点M,
∵⊙O是△ABC的外接圆,∠BAC=60°,
∴∠BOC=2∠BAC=120°,
又∵OB=OC,OM⊥BC,
∴∠COM=∠BOC=60°,MB=MC,
∴在Rt△COM中,∠OCM=30°,
∴OM=OC=1,CM=OM=,
∴BC=2CM=2,
故选:B.
4.解:∵AB为⊙O的直径,
∴∠ACB=90°.
∵OC=AC=5,
∴AB=2OC=10,
∴BC===5.
故选:D.
5.解:连接BD,
∵点A为弧CD的中点,
∴=,
∵∠ABC=28°,
∴∠DBC=2∠ABC=56°,
∴∠DAE=∠DBC=56°,
∵AD平分∠BAE,
∴∠BAE=2∠DAE=112°,
∵∠BAE=∠ABC+∠ACB,
∴∠ACB=∠BAE﹣∠ABC=112°﹣28°=84°,
故选:A.
6.解:∵AP=2<5,
∴点P在⊙A内部.
故选:C.
7.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
9.解:A、在同圆或等圆中,相等的圆心角所对的弧相等,故本选项说法不正确;
B、不在同一直线上的三个点确定一个圆,若这三个点在一条直线上,就不能确定圆,故本选项说法不正确;
C、周长相等半径就相等,半径相等的两个圆能重合,故本选项说法正确;
D、平分弦(不是直径)的直径垂直于弦,故本选项说法不正确;
故选:C.
10.解:如图,当四点在同一条直线上时,不能确定圆,当四点共圆时,只能作一个圆,当三点在同一直线上时,可以作三个圆,当四点不共圆时,且没有三点共线时,能确定四个圆.
故选:C.
11.解:△AOB中,OA=OB,∠ABO=25°,
∴∠AOB=180°﹣2∠ABO=130°,
∴∠ACB=∠AOB=65°,
故选:C.
12.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
13.解:连接OB、OC,
∵∠A=40°,
∴∠BOC=2∠A=80°,
∵E是边BC的中点,
∴=,
∴∠BOD=∠BOC=40°,
∵OB=OD,
∴∠D=×(180°﹣40°)=70°,
故答案为:70°.
14.解:延长BD交圆O于点G,连接CG,如图:
∵∠A=40°,
∴∠A=∠G=40°,
∵BG是⊙O的直径,
∴∠BCG=90°,
∵AB=AC,
∴∠BCA=∠CBA=(180°﹣40°)=70°,
∴∠DCG=20°,
∴∠BDC=∠G+∠DCG=40°+20°=60°,
故答案为:60°.
15.解:连接BE,
∵AD是△ABC的高,
∴∠ADC=90°,
∴AD===2,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠ABE=∠ADC,
∵∠E=∠C,
∴△ABE∽△ADC,
∴=,
∴=,
∴AB=,
故答案为:.
16.解:∵BC为直径,
∴∠BAC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=45°,
∵∠ACB=65°,
∴∠ABC=90°﹣65°=25°,
∵∠DBC=∠DAC=45°,
∴∠ABD=∠ABC+∠DBC=25°+45°=70°.
则∠ABD的度数为70°.
故答案为:70°.
17.解:连接BO并延长交⊙O于D,连接CD,
则∠BCD=90°,
∵∠BAC=30°,
∴∠D=∠BAC=30°,
∵BC=2,
∴BD=2BC=4,
故答案为:4.
18.解:①△ABC是锐角三角形,如图,
∵∠BOC=110°,
∴∠BAC=55°;
②△A′BC是钝角三角形,如图,
∵∠BAC+∠BA′C=180°,
∴∠BA′C=125°.
故答案为:55°或125.
19.解:连接AD,
∵∠BAC=120°,AB=AC=4,
∴∠C=∠ABC=(180°﹣∠BAC)=30°,
∴∠D=∠C=30°,
∵BD是直径,
∴∠BAD=90°
∴AB=2AB=8,
∴⊙O的半径为4,
故答案为:4.
20.解:连结AO,并延长交⊙O于E,连结EC,延长BD交AC于F,
∵AE为直径,
∴∠ACE=∠ABE=90°,
∵点D是△ABC高线的交点,
∴BF⊥AC,AG⊥BC,CD⊥AB,
∴∠CFB=∠CGA=90°,
∴∠FDG=360°﹣90°﹣90°﹣60°=120°,
∴∠ADB=∠FDG=120°,
∵∠ACE=∠CFB=90°,CD⊥AB,EB⊥AB,
∴CE∥DB,CD∥EB,
∴四边形CDBE为平行四边形,
∴CD=BE,
∵=,
∴∠ACB=∠AEB=60°,
∴∠EAB=90°﹣∠AEB=90°﹣60°=30°,
在Rt△ABE中,
BE=AB×tan30°=8×=,
∴CD=BE=.
故答案为:120°;.
21.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
22.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
23.(1)证明:∵AD⊥BC,
∴=,
∴∠ABC=∠ACB;
(2)解:连接OC,如图,
设OE=x,则DE=OD﹣OE=﹣﹣x,
在Rt△OEC中,CE2=OC2﹣OE2=()2﹣x2,
在Rt△CDE中,CE2=CD2﹣DE2=52﹣(﹣x)2,
∴()2﹣x2=52﹣(﹣x)2,解得x=,
∴CE==.
24.(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴=,即=,
解得,AF=.
25.解:(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,
∴BH=CH=BC=3,
即AH垂直平分BC,
∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,
即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,
∴EH=EF,
∵S△ABE=BH AE=AB EF,
∴==,
∴EH=AH=×4=,
由(1)得OH=AH﹣OA=4﹣=,
∴OE=﹣=.
期末复习自主提升训练(附答案)
1.已知⊙O的半径为5cm,P到圆心O的距离为6cm,则点P与⊙O的位置关系是( )
A.点P在圆外 B.点P在圆上 C.点P在圆内 D.不能确定
2.已知OA=4,以O为圆心,r为半径作⊙O.若使点A在⊙O内,则r的值可以是( )
A.2 B.3 C.4 D.5
3.如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
A.4 B.2 C.3 D.
4.如图,⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=AC=5,则BC长为( )
A.10 B.9 C.8 D.5
5.如图,△ABC内接于⊙O,其外角∠BAE的平分线交⊙O于点D,点A为弧CD的中点.若∠ABC=28°,则∠ACB的大小为( )
A.84° B.85° C.86° D.88°
6.若⊙A的半径为5,圆心A与点P的距离是,则点P与⊙A的位置关系是( )
A.P在⊙A上 B.P在⊙A外 C.P在⊙A内 D.不确定
7.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
9.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.过任意三点可以画一个圆
C.周长相等的圆是等圆 D.平分弦的直径垂直于弦
10.平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
11.如图所示,⊙O是△ABC的外接圆,已知∠ABO=25°,则∠ACB的大小为( )
A.50° B.55° C.65° D.75°
12.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
13.如图,△ABC内接于⊙O,∠A=40°,E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的度数是 .
14.如图AB=AC,∠A=40°,O是△ABC外接圆圆心,BO交AC于点D,则∠BDC= .
15.如图,△ABC是⊙O的内接三角形,AD是△ABC的高,AE是⊙O的直径,且AE=4,若CD=1,AC=3,则AB的长为 .
16.如图,△BAC是⊙O的内接三角形,BC为直径,AD平分∠BAC,连接BD、CD,若∠ACB=65°,则∠ABD的度数为 .
17.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则⊙O的直径长等于 .
18.点O是△ABC的外心,若∠BOC=110°,则∠BAC为 °.
19.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为 .
20.如图,⊙O是锐角三角形ABC的外接圆,AB=8,∠ACB=60°,且BC>AC,点D是△ABC高线的交点,连接AD,BD,CD,则∠ADB的度数为 ,CD的长为 .
21.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
22.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
23.如图,已知⊙O是△ABC的外接圆,直径AD与BC垂直,垂足为点E.
(1)求证:∠ABC=∠ACB;
(2)连接OB,CD,若OB=,CD=5,求CE的长.
24.如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
25.△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
参考答案
1.解:∵⊙O的半径为5cm,点P到圆心O的距离为6cm,
∴OP>⊙O的半径,
∴点P在⊙O外.
故选:A.
2.解:∵已知OA=4,以O为圆心,r为半径作⊙O.若使点A在⊙O内,
∴点A到圆心的距离应该小于圆的半径,
∴圆的半径应该大于4.
故选:D.
3.解:过点O作OM⊥BC,交BC于点M,
∵⊙O是△ABC的外接圆,∠BAC=60°,
∴∠BOC=2∠BAC=120°,
又∵OB=OC,OM⊥BC,
∴∠COM=∠BOC=60°,MB=MC,
∴在Rt△COM中,∠OCM=30°,
∴OM=OC=1,CM=OM=,
∴BC=2CM=2,
故选:B.
4.解:∵AB为⊙O的直径,
∴∠ACB=90°.
∵OC=AC=5,
∴AB=2OC=10,
∴BC===5.
故选:D.
5.解:连接BD,
∵点A为弧CD的中点,
∴=,
∵∠ABC=28°,
∴∠DBC=2∠ABC=56°,
∴∠DAE=∠DBC=56°,
∵AD平分∠BAE,
∴∠BAE=2∠DAE=112°,
∵∠BAE=∠ABC+∠ACB,
∴∠ACB=∠BAE﹣∠ABC=112°﹣28°=84°,
故选:A.
6.解:∵AP=2<5,
∴点P在⊙A内部.
故选:C.
7.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
9.解:A、在同圆或等圆中,相等的圆心角所对的弧相等,故本选项说法不正确;
B、不在同一直线上的三个点确定一个圆,若这三个点在一条直线上,就不能确定圆,故本选项说法不正确;
C、周长相等半径就相等,半径相等的两个圆能重合,故本选项说法正确;
D、平分弦(不是直径)的直径垂直于弦,故本选项说法不正确;
故选:C.
10.解:如图,当四点在同一条直线上时,不能确定圆,当四点共圆时,只能作一个圆,当三点在同一直线上时,可以作三个圆,当四点不共圆时,且没有三点共线时,能确定四个圆.
故选:C.
11.解:△AOB中,OA=OB,∠ABO=25°,
∴∠AOB=180°﹣2∠ABO=130°,
∴∠ACB=∠AOB=65°,
故选:C.
12.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
13.解:连接OB、OC,
∵∠A=40°,
∴∠BOC=2∠A=80°,
∵E是边BC的中点,
∴=,
∴∠BOD=∠BOC=40°,
∵OB=OD,
∴∠D=×(180°﹣40°)=70°,
故答案为:70°.
14.解:延长BD交圆O于点G,连接CG,如图:
∵∠A=40°,
∴∠A=∠G=40°,
∵BG是⊙O的直径,
∴∠BCG=90°,
∵AB=AC,
∴∠BCA=∠CBA=(180°﹣40°)=70°,
∴∠DCG=20°,
∴∠BDC=∠G+∠DCG=40°+20°=60°,
故答案为:60°.
15.解:连接BE,
∵AD是△ABC的高,
∴∠ADC=90°,
∴AD===2,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠ABE=∠ADC,
∵∠E=∠C,
∴△ABE∽△ADC,
∴=,
∴=,
∴AB=,
故答案为:.
16.解:∵BC为直径,
∴∠BAC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=45°,
∵∠ACB=65°,
∴∠ABC=90°﹣65°=25°,
∵∠DBC=∠DAC=45°,
∴∠ABD=∠ABC+∠DBC=25°+45°=70°.
则∠ABD的度数为70°.
故答案为:70°.
17.解:连接BO并延长交⊙O于D,连接CD,
则∠BCD=90°,
∵∠BAC=30°,
∴∠D=∠BAC=30°,
∵BC=2,
∴BD=2BC=4,
故答案为:4.
18.解:①△ABC是锐角三角形,如图,
∵∠BOC=110°,
∴∠BAC=55°;
②△A′BC是钝角三角形,如图,
∵∠BAC+∠BA′C=180°,
∴∠BA′C=125°.
故答案为:55°或125.
19.解:连接AD,
∵∠BAC=120°,AB=AC=4,
∴∠C=∠ABC=(180°﹣∠BAC)=30°,
∴∠D=∠C=30°,
∵BD是直径,
∴∠BAD=90°
∴AB=2AB=8,
∴⊙O的半径为4,
故答案为:4.
20.解:连结AO,并延长交⊙O于E,连结EC,延长BD交AC于F,
∵AE为直径,
∴∠ACE=∠ABE=90°,
∵点D是△ABC高线的交点,
∴BF⊥AC,AG⊥BC,CD⊥AB,
∴∠CFB=∠CGA=90°,
∴∠FDG=360°﹣90°﹣90°﹣60°=120°,
∴∠ADB=∠FDG=120°,
∵∠ACE=∠CFB=90°,CD⊥AB,EB⊥AB,
∴CE∥DB,CD∥EB,
∴四边形CDBE为平行四边形,
∴CD=BE,
∵=,
∴∠ACB=∠AEB=60°,
∴∠EAB=90°﹣∠AEB=90°﹣60°=30°,
在Rt△ABE中,
BE=AB×tan30°=8×=,
∴CD=BE=.
故答案为:120°;.
21.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
22.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
23.(1)证明:∵AD⊥BC,
∴=,
∴∠ABC=∠ACB;
(2)解:连接OC,如图,
设OE=x,则DE=OD﹣OE=﹣﹣x,
在Rt△OEC中,CE2=OC2﹣OE2=()2﹣x2,
在Rt△CDE中,CE2=CD2﹣DE2=52﹣(﹣x)2,
∴()2﹣x2=52﹣(﹣x)2,解得x=,
∴CE==.
24.(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴=,即=,
解得,AF=.
25.解:(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,
∴BH=CH=BC=3,
即AH垂直平分BC,
∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,
即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,
∴EH=EF,
∵S△ABE=BH AE=AB EF,
∴==,
∴EH=AH=×4=,
由(1)得OH=AH﹣OA=4﹣=,
∴OE=﹣=.
