3.9弧长及扇形面积 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析)
文档属性
| 名称 | 3.9弧长及扇形面积 期末复习自主提升训练 2021-2022学年北师大版九年级数学下册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 12:00:04 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.9弧长及扇形面积》
期末复习自主提升训练(附答案)
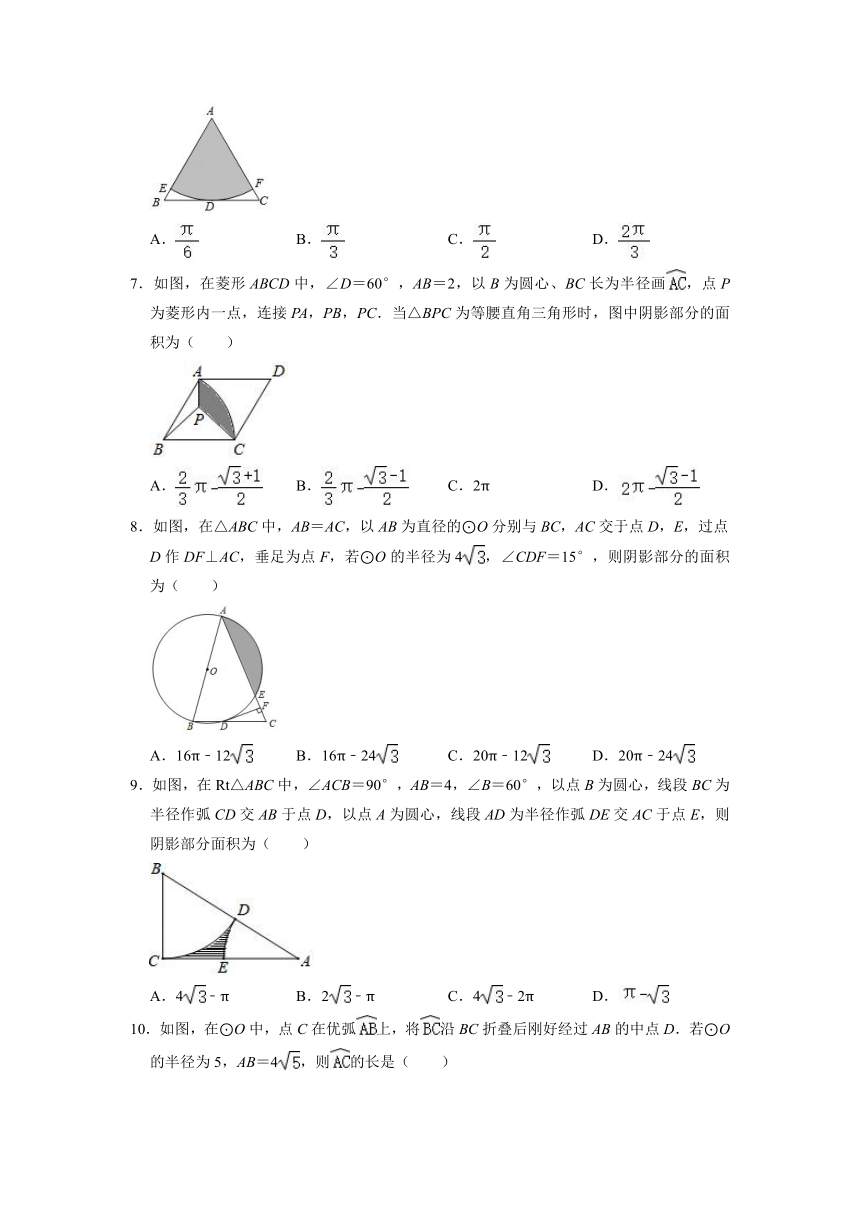
1.一条弧所对的圆心角为135°,弧长等于半径为3cm的圆的周长的5倍,则这条弧的半径为( )
A.45cm B.40cm C.35cm D.30cm
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上.已知消防车道半径OC=12m,消防车道宽AC=4m,∠AOB=120°,则弯道外边缘的长为( )
A.8πm B.4πm C.πm D.πm
3.将一半径为6的圆形纸片,沿着两条半径剪开形成两个扇形.若其中一个扇形的弧长为5π,则另一个扇形的圆心角度数是多少?( )
A.30 B.60 C.105 D.210
4.如图,在矩形ABCD中,AB=2,BC=4,以点A为圆心,AD长为半径画弧交BC于点E,连接AE,则阴影部分的面积为( )
A.6﹣ B.4﹣ C.6﹣ D.6﹣
5.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A. B. C.π﹣1 D.π﹣2
6.如图,在边长为2的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,在菱形ABCD中,∠D=60°,AB=2,以B为圆心、BC长为半径画,点P为菱形内一点,连接PA,PB,PC.当△BPC为等腰直角三角形时,图中阴影部分的面积为( )
A. B. C.2π D.
8.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12 B.16π﹣24 C.20π﹣12 D.20π﹣24
9.如图,在Rt△ABC中,∠ACB=90°,AB=4,∠B=60°,以点B为圆心,线段BC为半径作弧CD交AB于点D,以点A为圆心,线段AD为半径作弧DE交AC于点E,则阴影部分面积为( )
A.4﹣π B.2﹣π C.4﹣2π D.
10.如图,在⊙O中,点C在优弧上,将沿BC折叠后刚好经过AB的中点D.若⊙O的半径为5,AB=4,则的长是( )
A. B. C. D.4π
11.一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是 cm.
12.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2.以点C为圆心,CB长为半径画弧,分别交AC,AB于点D,E,则图中阴影部分的面积为 (结果保留π).
13.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
14.如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,且∠ACB=60°,若点M,N分别是AB,BC的中点,则图中阴影部分面积的最大值是 .
15.如图,正方形ABCD的边长为2,分别以B,C为圆心,以正方形的边长为半径的圆相交于点P,那么图中阴影部分的面积为 .
16.如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心、BC长为半径画弧交AC于点F,则图中阴影部分的面积是 .
17.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
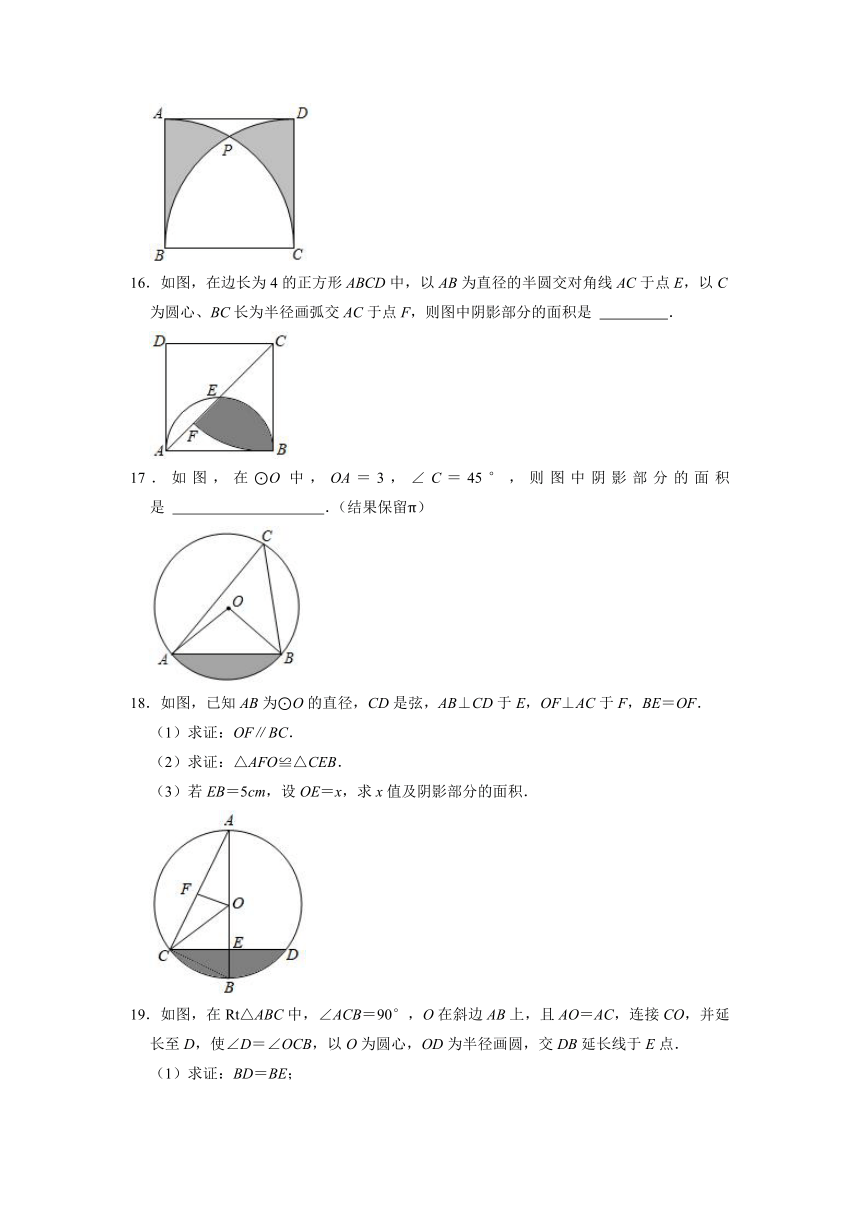
18.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
19.如图,在Rt△ABC中,∠ACB=90°,O在斜边AB上,且AO=AC,连接CO,并延长至D,使∠D=∠OCB,以O为圆心,OD为半径画圆,交DB延长线于E点.
(1)求证:BD=BE;
(2)已知AC=1cm,BC=cm.
①连接CE,过B作BF⊥EC于F点,求线段BF的长;
②求图中阴影部分面积.
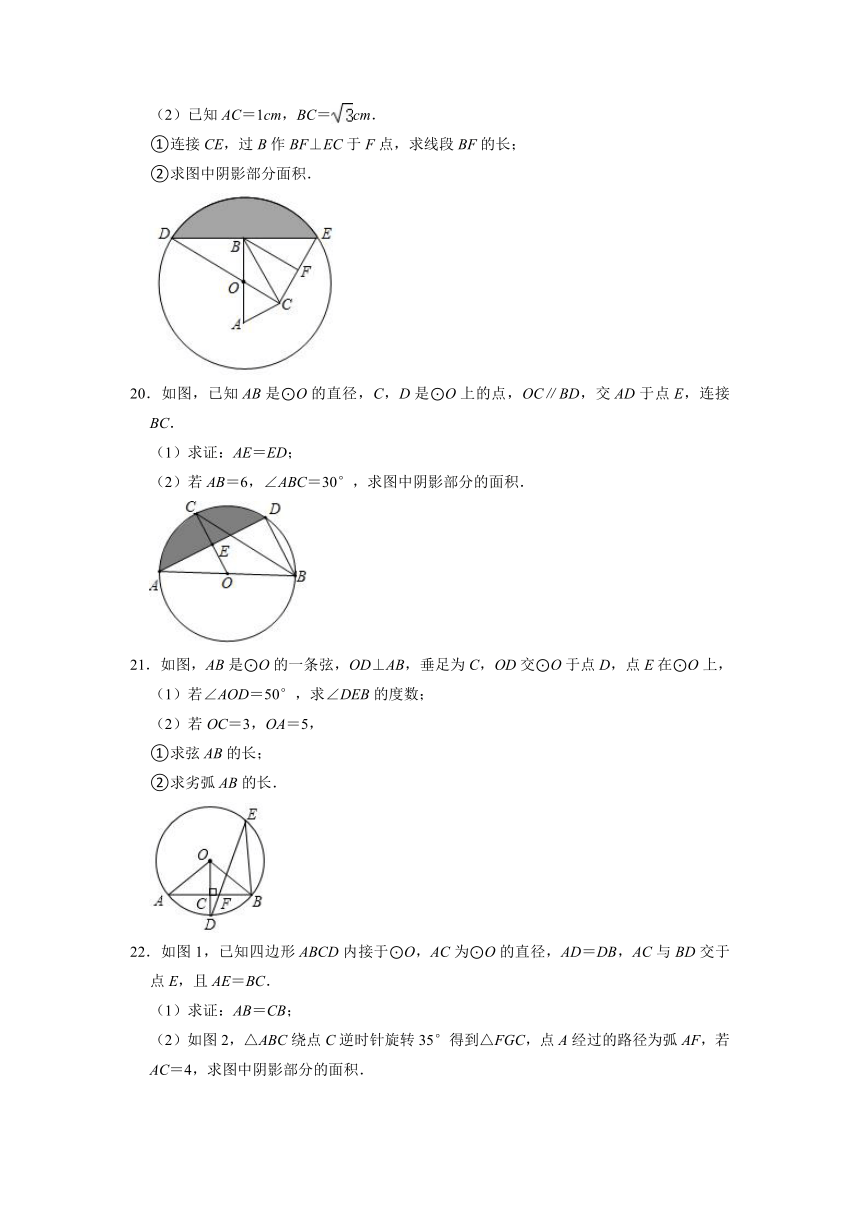
20.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
21.如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在⊙O上,
(1)若∠AOD=50°,求∠DEB的度数;
(2)若OC=3,OA=5,
①求弦AB的长;
②求劣弧AB的长.
22.如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
参考答案
1.解:设弧所在圆的半径为rcm,
由题意得,=2π×3×5,
解得,r=40.
故选:B.
2.解:∵OC=12m,AC=4m,
∴OA=OC+AC=12+4=16(m),
∵∠AOB=120°,
∴弯道外边缘的长为:=(m),
故选:C.
3.解:由题意可求得圆形的周长C=2π×6=12π,
其中一个扇形的弧长L1=5π,则另一个扇形的弧长L2=12π﹣5π=7π,
设另一个扇形的圆心角度数为n°,
根据弧长公式:L=,有:
7π=,解得n=210,
故选:D.
4.解:∵四边形ABCD是矩形,AD=BC=4,
∴∠B=∠DAB=90°,AD=AE=4,
∵AB=2,
∴cos∠BAE==,
∴∠BAE=30°,∠EAD=60°,
∴BE=AE=2,
∴阴影部分的面积S=S矩形ABCD﹣S△ABE﹣S扇形EAD
=2×4﹣××2﹣
=6﹣.
故选:A.
5.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
6.解:连接AD,如图所示:
∵D是BC边上的中点,
∴AD⊥BC,
∵△ABC是等边三角形,
∴∠B=60°,BC=AB=2,
∴AD=AB sin60°=2×=,
∴阴影部分的面积==.
故选:C.
7.解:连接AC,延长AP,交BC于E,
在菱形ABCD中,∠D=60°,AB=2,
∴∠ABC=∠D=60°,AB=BC=2,
∴△ABC是等边三角形,
∴AB=AC,
在△APB和△APC中,
,
∴△APB≌△APC(SSS),
∴∠PAB=∠PAC,
∴AE⊥BC,BE=CE=1,
∵△BPC为等腰直角三角形,
∴PE=BC=1,
在Rt△ABE中,AE=AB=,
∴AP=﹣1,
∴S阴影=S扇形ABC﹣S△PAB﹣S△PBC=﹣(﹣1)×1﹣=π﹣,
故选:A.
8.解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=sin30°×OA=2,
AH=cos30°×OA=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
9.解:∵在Rt△ABC中,∠ACB=90°,AB=4,∠B=60°,
∴∠A=30°,BC=AB=2,AC===2,
∴阴影部分的面积S=S△ABC﹣S扇形BCD﹣S扇形ADE=﹣﹣=2﹣π,
故选:B.
10.解:连接AC,OB,OD,CD,作CF⊥AB于点F,作OE⊥CF于点E,
由垂定理可知OD⊥AB于点D,AD=BD==.
又OB=5,
∴OD===,
∵CA、CD所对的圆周角为∠CBA、∠CBD,且∠CBA=∠CBD,
∴CA=CD,△CAD为等腰三角形.
∵CF⊥AB,
∴AF=DF==,
又四边形ODFE为矩形且OD=DF=,
∴四边形ODFE为正方形.
∴,
∴CE===2,
∴CF=CE+EF=3=BF,
故△CFB为等腰直角三角形,∠CBA=45°,
∴所对的圆心角为90°,
∴==.
故选:A.
11.解:设扇形的半径为rcm,由题意得,
=8π,
解得r=10(cm),
故答案为:10.
12.解:连接CE,
∵∠A=30°,
∴∠CBA=90°﹣∠A=60°,
∵CE=CB,
∴△CBE为等边三角形,
∴∠ECB=60°,BE=BC=2,
∴S扇形CBE==π
∵S△BCE=BC2=,
∴阴影部分的面积为π﹣.
故答案为:π﹣.
13.解:∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC=BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积==,
故答案为:.
14.解:连接OA、OB、OM,如图,
∵∠ACB=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,
∴OM⊥AB,
∴tan30°=,
∴OM=×=1,
∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,
∴△MBN∽△ABC,
∴=()2=,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
故答案为:﹣.
15.解:连接PB、PC,作PF⊥BC于F,
∵PB=PC=BC,
∴△PBC为等边三角形,
∴∠PBC=60°,∠PBA=30°,
∴BF=PB cos60°=PB=1,PF=PB sin60°=,
则图中阴影部分的面积=[扇形ABP的面积﹣(扇形BPC的面积﹣△BPC的面积)]×2
=[﹣(﹣×2×)]×2=2﹣,
故答案为:2﹣.
16.解:连接BE,
∵AB为直径,
∴BE⊥AC,
∵AB=BC=4,∠ABC=90°,
∴BE=AE=CE,
∴S弓形AE=S弓形BE,
∴图中阴影部分的面积=S半圆﹣(S半圆﹣S△ABE)﹣(S△ABC﹣S扇形CBF)
=π×22﹣(﹣)﹣(﹣)
=3π﹣6,
故答案为3π﹣6.
17.解:∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣.
故答案为:π﹣.
18.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OF∥BC;
(2)证明:∵AB⊥CD,
∴=,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OF∥BC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB,
∴OA=BC=10cm,
∴CE===5cm,
∴CD=2CE=10cm,
∵OB=x+5,
∴OE=OB﹣5=10﹣5=5cm,
∵cos∠COE===,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:=cm2
△COD的面积是:CD OE==25cm2
∴阴影部分的面积是:(﹣25)cm2.
19.(1)证明:∵AO=AC,
∴∠ACO=∠AOC,
∵∠D=∠OCB,∠BOD=∠AOC,
∴∠ACO+∠OCB=∠BOD+∠D,
∵∠ACB=90°,
∴∠BOD+∠D=90°,
∴OB⊥DE,
∴BD=BE;
(2)解:①在Rt△ABC中,∠ACB=90°,AC=1cm,BC=cm.
∴tan∠ABC===,
∴∠ABC=30°,
∴AB=2AC=2,∠A=60°,
∵OA=AC,
∴△AOC为等边三角形,
∴OC=AC=1cm,∠AOC=60°,
∴∠D=∠OCB=30°,OB=AB﹣OA=1,
∴OD=2OB=2,
∴CD=OD+OC=3,
∵∠D=∠OCB,
∴BD=BC,
∵BD=BE,
∴BC=BE,
∴∠BCE=∠BEC,
∴∠D+∠BEC=∠DCE=90°,
∵BF⊥CE,
∴BF∥CD,
∵BD=BE,
∴BF=CD=;
②解:连接OE,
∵OD=2、OB=1,
∴BD=,
则DE=2BD=2,
∵OD=OE,
∴∠D=∠OED=30°,
∴∠DOE=120°,
S阴影=S扇形ODE﹣S△ODE=﹣×2×1=π﹣.
20.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°,
∵OC⊥AD,
∴=,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE==,
∴S阴影=S扇形AOD﹣S△AOD=﹣×=3π﹣.
21.解:(1)∵OD⊥AB,
∴=,
∴∠DEB=∠BOD=∠AOD=×50°=25°.
(2)①∵OC=3,OA=5,
∴AC=4,
∵OD⊥AB,
∴==,
∴AC=BC=AB=4,
∴AB=8;
②∵∠AOD的正弦值是==0.8,
∴∠AOD=53°,
∴∠AOB=106°,
∵OA=5,
∴的长===.
22.(1)证明:∵AD=BD,∠DAE=∠DBC,AE=BC,
∴△ADE≌△BDC(SAS),
∴∠ADE=∠BDC,
∴=.
∴AB=BC.
(2)解:S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF==
期末复习自主提升训练(附答案)
1.一条弧所对的圆心角为135°,弧长等于半径为3cm的圆的周长的5倍,则这条弧的半径为( )
A.45cm B.40cm C.35cm D.30cm
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上.已知消防车道半径OC=12m,消防车道宽AC=4m,∠AOB=120°,则弯道外边缘的长为( )
A.8πm B.4πm C.πm D.πm
3.将一半径为6的圆形纸片,沿着两条半径剪开形成两个扇形.若其中一个扇形的弧长为5π,则另一个扇形的圆心角度数是多少?( )
A.30 B.60 C.105 D.210
4.如图,在矩形ABCD中,AB=2,BC=4,以点A为圆心,AD长为半径画弧交BC于点E,连接AE,则阴影部分的面积为( )
A.6﹣ B.4﹣ C.6﹣ D.6﹣
5.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A. B. C.π﹣1 D.π﹣2
6.如图,在边长为2的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,在菱形ABCD中,∠D=60°,AB=2,以B为圆心、BC长为半径画,点P为菱形内一点,连接PA,PB,PC.当△BPC为等腰直角三角形时,图中阴影部分的面积为( )
A. B. C.2π D.
8.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12 B.16π﹣24 C.20π﹣12 D.20π﹣24
9.如图,在Rt△ABC中,∠ACB=90°,AB=4,∠B=60°,以点B为圆心,线段BC为半径作弧CD交AB于点D,以点A为圆心,线段AD为半径作弧DE交AC于点E,则阴影部分面积为( )
A.4﹣π B.2﹣π C.4﹣2π D.
10.如图,在⊙O中,点C在优弧上,将沿BC折叠后刚好经过AB的中点D.若⊙O的半径为5,AB=4,则的长是( )
A. B. C. D.4π
11.一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是 cm.
12.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2.以点C为圆心,CB长为半径画弧,分别交AC,AB于点D,E,则图中阴影部分的面积为 (结果保留π).
13.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
14.如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,且∠ACB=60°,若点M,N分别是AB,BC的中点,则图中阴影部分面积的最大值是 .
15.如图,正方形ABCD的边长为2,分别以B,C为圆心,以正方形的边长为半径的圆相交于点P,那么图中阴影部分的面积为 .
16.如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心、BC长为半径画弧交AC于点F,则图中阴影部分的面积是 .
17.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
18.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
19.如图,在Rt△ABC中,∠ACB=90°,O在斜边AB上,且AO=AC,连接CO,并延长至D,使∠D=∠OCB,以O为圆心,OD为半径画圆,交DB延长线于E点.
(1)求证:BD=BE;
(2)已知AC=1cm,BC=cm.
①连接CE,过B作BF⊥EC于F点,求线段BF的长;
②求图中阴影部分面积.
20.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
21.如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在⊙O上,
(1)若∠AOD=50°,求∠DEB的度数;
(2)若OC=3,OA=5,
①求弦AB的长;
②求劣弧AB的长.
22.如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
参考答案
1.解:设弧所在圆的半径为rcm,
由题意得,=2π×3×5,
解得,r=40.
故选:B.
2.解:∵OC=12m,AC=4m,
∴OA=OC+AC=12+4=16(m),
∵∠AOB=120°,
∴弯道外边缘的长为:=(m),
故选:C.
3.解:由题意可求得圆形的周长C=2π×6=12π,
其中一个扇形的弧长L1=5π,则另一个扇形的弧长L2=12π﹣5π=7π,
设另一个扇形的圆心角度数为n°,
根据弧长公式:L=,有:
7π=,解得n=210,
故选:D.
4.解:∵四边形ABCD是矩形,AD=BC=4,
∴∠B=∠DAB=90°,AD=AE=4,
∵AB=2,
∴cos∠BAE==,
∴∠BAE=30°,∠EAD=60°,
∴BE=AE=2,
∴阴影部分的面积S=S矩形ABCD﹣S△ABE﹣S扇形EAD
=2×4﹣××2﹣
=6﹣.
故选:A.
5.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
6.解:连接AD,如图所示:
∵D是BC边上的中点,
∴AD⊥BC,
∵△ABC是等边三角形,
∴∠B=60°,BC=AB=2,
∴AD=AB sin60°=2×=,
∴阴影部分的面积==.
故选:C.
7.解:连接AC,延长AP,交BC于E,
在菱形ABCD中,∠D=60°,AB=2,
∴∠ABC=∠D=60°,AB=BC=2,
∴△ABC是等边三角形,
∴AB=AC,
在△APB和△APC中,
,
∴△APB≌△APC(SSS),
∴∠PAB=∠PAC,
∴AE⊥BC,BE=CE=1,
∵△BPC为等腰直角三角形,
∴PE=BC=1,
在Rt△ABE中,AE=AB=,
∴AP=﹣1,
∴S阴影=S扇形ABC﹣S△PAB﹣S△PBC=﹣(﹣1)×1﹣=π﹣,
故选:A.
8.解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=sin30°×OA=2,
AH=cos30°×OA=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
9.解:∵在Rt△ABC中,∠ACB=90°,AB=4,∠B=60°,
∴∠A=30°,BC=AB=2,AC===2,
∴阴影部分的面积S=S△ABC﹣S扇形BCD﹣S扇形ADE=﹣﹣=2﹣π,
故选:B.
10.解:连接AC,OB,OD,CD,作CF⊥AB于点F,作OE⊥CF于点E,
由垂定理可知OD⊥AB于点D,AD=BD==.
又OB=5,
∴OD===,
∵CA、CD所对的圆周角为∠CBA、∠CBD,且∠CBA=∠CBD,
∴CA=CD,△CAD为等腰三角形.
∵CF⊥AB,
∴AF=DF==,
又四边形ODFE为矩形且OD=DF=,
∴四边形ODFE为正方形.
∴,
∴CE===2,
∴CF=CE+EF=3=BF,
故△CFB为等腰直角三角形,∠CBA=45°,
∴所对的圆心角为90°,
∴==.
故选:A.
11.解:设扇形的半径为rcm,由题意得,
=8π,
解得r=10(cm),
故答案为:10.
12.解:连接CE,
∵∠A=30°,
∴∠CBA=90°﹣∠A=60°,
∵CE=CB,
∴△CBE为等边三角形,
∴∠ECB=60°,BE=BC=2,
∴S扇形CBE==π
∵S△BCE=BC2=,
∴阴影部分的面积为π﹣.
故答案为:π﹣.
13.解:∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC=BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积==,
故答案为:.
14.解:连接OA、OB、OM,如图,
∵∠ACB=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,
∴OM⊥AB,
∴tan30°=,
∴OM=×=1,
∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,
∴△MBN∽△ABC,
∴=()2=,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
故答案为:﹣.
15.解:连接PB、PC,作PF⊥BC于F,
∵PB=PC=BC,
∴△PBC为等边三角形,
∴∠PBC=60°,∠PBA=30°,
∴BF=PB cos60°=PB=1,PF=PB sin60°=,
则图中阴影部分的面积=[扇形ABP的面积﹣(扇形BPC的面积﹣△BPC的面积)]×2
=[﹣(﹣×2×)]×2=2﹣,
故答案为:2﹣.
16.解:连接BE,
∵AB为直径,
∴BE⊥AC,
∵AB=BC=4,∠ABC=90°,
∴BE=AE=CE,
∴S弓形AE=S弓形BE,
∴图中阴影部分的面积=S半圆﹣(S半圆﹣S△ABE)﹣(S△ABC﹣S扇形CBF)
=π×22﹣(﹣)﹣(﹣)
=3π﹣6,
故答案为3π﹣6.
17.解:∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣.
故答案为:π﹣.
18.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OF∥BC;
(2)证明:∵AB⊥CD,
∴=,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OF∥BC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB,
∴OA=BC=10cm,
∴CE===5cm,
∴CD=2CE=10cm,
∵OB=x+5,
∴OE=OB﹣5=10﹣5=5cm,
∵cos∠COE===,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:=cm2
△COD的面积是:CD OE==25cm2
∴阴影部分的面积是:(﹣25)cm2.
19.(1)证明:∵AO=AC,
∴∠ACO=∠AOC,
∵∠D=∠OCB,∠BOD=∠AOC,
∴∠ACO+∠OCB=∠BOD+∠D,
∵∠ACB=90°,
∴∠BOD+∠D=90°,
∴OB⊥DE,
∴BD=BE;
(2)解:①在Rt△ABC中,∠ACB=90°,AC=1cm,BC=cm.
∴tan∠ABC===,
∴∠ABC=30°,
∴AB=2AC=2,∠A=60°,
∵OA=AC,
∴△AOC为等边三角形,
∴OC=AC=1cm,∠AOC=60°,
∴∠D=∠OCB=30°,OB=AB﹣OA=1,
∴OD=2OB=2,
∴CD=OD+OC=3,
∵∠D=∠OCB,
∴BD=BC,
∵BD=BE,
∴BC=BE,
∴∠BCE=∠BEC,
∴∠D+∠BEC=∠DCE=90°,
∵BF⊥CE,
∴BF∥CD,
∵BD=BE,
∴BF=CD=;
②解:连接OE,
∵OD=2、OB=1,
∴BD=,
则DE=2BD=2,
∵OD=OE,
∴∠D=∠OED=30°,
∴∠DOE=120°,
S阴影=S扇形ODE﹣S△ODE=﹣×2×1=π﹣.
20.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°,
∵OC⊥AD,
∴=,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE==,
∴S阴影=S扇形AOD﹣S△AOD=﹣×=3π﹣.
21.解:(1)∵OD⊥AB,
∴=,
∴∠DEB=∠BOD=∠AOD=×50°=25°.
(2)①∵OC=3,OA=5,
∴AC=4,
∵OD⊥AB,
∴==,
∴AC=BC=AB=4,
∴AB=8;
②∵∠AOD的正弦值是==0.8,
∴∠AOD=53°,
∴∠AOB=106°,
∵OA=5,
∴的长===.
22.(1)证明:∵AD=BD,∠DAE=∠DBC,AE=BC,
∴△ADE≌△BDC(SAS),
∴∠ADE=∠BDC,
∴=.
∴AB=BC.
(2)解:S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF==
