华东师大版数学九年级上册 24.4 解直角三角形(1)课件(共19张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 24.4 解直角三角形(1)课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 16:29:00 | ||
图片预览






文档简介
(共19张PPT)
A
B
C
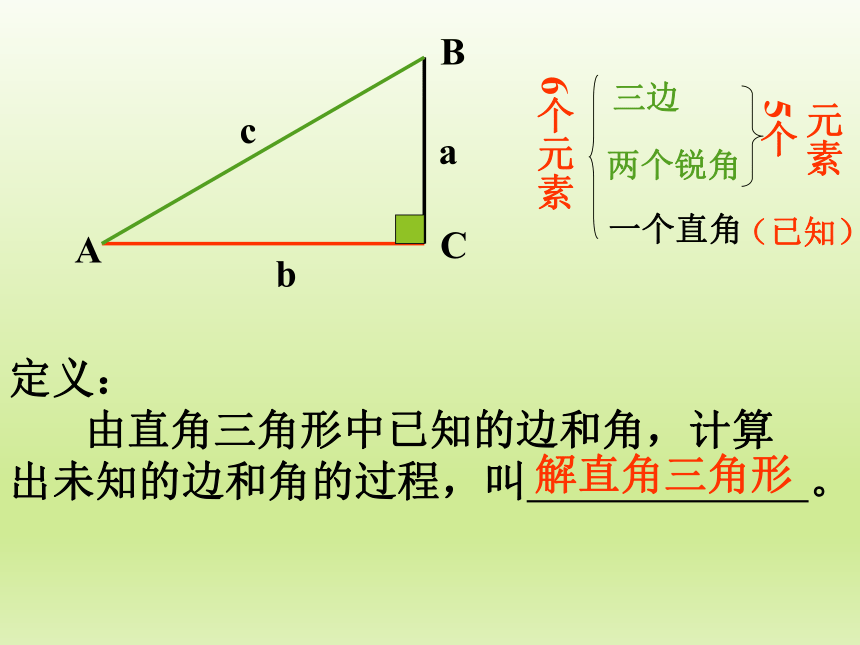
6个元素
三边
两个锐角
一个直角
(已知)
元素
5个
定义:
由直角三角形中已知的边和角,计算出未知的边和角的过程,叫 。
解直角三角形
a
b
c
解直角三角形的依据:
(1)三边之间的关系:
B
C
a
b
c
A
(2)锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
sinA=
cosA =
tanA=
cotA=
其中
A可换
成B
这三个关系式中,每个关系式都包含 元素,已知其中 元素就可以求出 __________。
三个
两个
第三个元素
例1 在△ABC中,∠C=90°,c=2,∠B=30°,解这个直角三角形 .
A
B
C
a
b
c
2
30°
例2 :在△ABC中,∠C=90°, ,
,求∠A、∠B、c边.
A
B
C
a
b
c
2
例3 在△ABC中,∠C=90°,b=35,c=45,(cos39°=0.7778),解直角三角形。
A
B
C
a
b
c
35
45
已知斜边求直边,
已知直边求直边,
已知两边求一边,
已知两边求一角,
已知锐角求锐角,
已知直边求斜边,
计算方法要选择,
正弦余弦很方便;
正切余切理当然;
函数关系要选好;
勾股定理最方便;
互余关系要记好;
用除还需正余弦;
能用乘法不用除。
优选关系式
让我们来认识几个概念:
坡角
试一试:
(1)升国旗时,某同学站在离旗杆底部20米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°若双眼离地面1.5米,则旗杆高度为 米(用含根号式子表示)
(2)某地下车库的入口处有斜坡AB,其坡度i=1:1.5。则AB= 米
(3)在坡角为30°的楼梯表面铺地毯,则地毯的长度至少需( )
A、 4m B、 6m
C、(6+2 )m D、(2+2 )m
例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。
尝试一下:
你还有其它方法吗?请同学们试着用这两种方法做做看。 (小组合作)
例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。
例5、 如图所示,一艘渔船以20千米/小时的速度向正北方向航行,在A处看见灯塔C在船的北偏东30°,半小时后,渔船行至B处,看见灯塔C在船的北偏东60°,已知C的周围7千米以内有暗礁,问这艘船继续向北航行是否有触礁的危险
解:当C到AB的距离CD≤ 7(千米)时,渔船有触礁的危险。
做一做: 在天空位置C处有一个已悬空静止的热气球,热气球上的人测得地面上A点的俯角为45°,测得地面上B点的俯角为60°,已知AB=20m,点C和直线AB在同一铅垂平面上,求热气球离地面高度(结果保留根号)
(1)求直角三角形中未知角、边时,先画出示意图,尽可能直接找出与已知角、边的关系来求解。
(2)解决实际问题时,先将实物模型转化为几何图形,如果示意图不是直角三角形时,添加适当的辅助线,画出直角三角形来求解。
学习永远是件快乐而有趣的事!
多彩的数学世界及其变换的魅力将把你引入一个奇妙的境界!
一棵老榆树上有两个鸟巢,方方搬来一个8米长的长梯,架在高的那个鸟巢的树枝上,梯子与地面成60°角,接着又架在低的那个鸟巢的树枝上,梯子与地成45°角,请问两个鸟巢分别离地多高 方方蹬梯子到低的那个鸟巢,照理应比爬到高的鸟巢快一些,可实际没快,为什么?
探究活动:
A
B
C
6个元素
三边
两个锐角
一个直角
(已知)
元素
5个
定义:
由直角三角形中已知的边和角,计算出未知的边和角的过程,叫 。
解直角三角形
a
b
c
解直角三角形的依据:
(1)三边之间的关系:
B
C
a
b
c
A
(2)锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
sinA=
cosA =
tanA=
cotA=
其中
A可换
成B
这三个关系式中,每个关系式都包含 元素,已知其中 元素就可以求出 __________。
三个
两个
第三个元素
例1 在△ABC中,∠C=90°,c=2,∠B=30°,解这个直角三角形 .
A
B
C
a
b
c
2
30°
例2 :在△ABC中,∠C=90°, ,
,求∠A、∠B、c边.
A
B
C
a
b
c
2
例3 在△ABC中,∠C=90°,b=35,c=45,(cos39°=0.7778),解直角三角形。
A
B
C
a
b
c
35
45
已知斜边求直边,
已知直边求直边,
已知两边求一边,
已知两边求一角,
已知锐角求锐角,
已知直边求斜边,
计算方法要选择,
正弦余弦很方便;
正切余切理当然;
函数关系要选好;
勾股定理最方便;
互余关系要记好;
用除还需正余弦;
能用乘法不用除。
优选关系式
让我们来认识几个概念:
坡角
试一试:
(1)升国旗时,某同学站在离旗杆底部20米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°若双眼离地面1.5米,则旗杆高度为 米(用含根号式子表示)
(2)某地下车库的入口处有斜坡AB,其坡度i=1:1.5。则AB= 米
(3)在坡角为30°的楼梯表面铺地毯,则地毯的长度至少需( )
A、 4m B、 6m
C、(6+2 )m D、(2+2 )m
例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。
尝试一下:
你还有其它方法吗?请同学们试着用这两种方法做做看。 (小组合作)
例4: 如图,在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。
例5、 如图所示,一艘渔船以20千米/小时的速度向正北方向航行,在A处看见灯塔C在船的北偏东30°,半小时后,渔船行至B处,看见灯塔C在船的北偏东60°,已知C的周围7千米以内有暗礁,问这艘船继续向北航行是否有触礁的危险
解:当C到AB的距离CD≤ 7(千米)时,渔船有触礁的危险。
做一做: 在天空位置C处有一个已悬空静止的热气球,热气球上的人测得地面上A点的俯角为45°,测得地面上B点的俯角为60°,已知AB=20m,点C和直线AB在同一铅垂平面上,求热气球离地面高度(结果保留根号)
(1)求直角三角形中未知角、边时,先画出示意图,尽可能直接找出与已知角、边的关系来求解。
(2)解决实际问题时,先将实物模型转化为几何图形,如果示意图不是直角三角形时,添加适当的辅助线,画出直角三角形来求解。
学习永远是件快乐而有趣的事!
多彩的数学世界及其变换的魅力将把你引入一个奇妙的境界!
一棵老榆树上有两个鸟巢,方方搬来一个8米长的长梯,架在高的那个鸟巢的树枝上,梯子与地面成60°角,接着又架在低的那个鸟巢的树枝上,梯子与地成45°角,请问两个鸟巢分别离地多高 方方蹬梯子到低的那个鸟巢,照理应比爬到高的鸟巢快一些,可实际没快,为什么?
探究活动:
