华东师大版数学九年级上册 23.6.2 图形的变换与坐标教案
文档属性
| 名称 | 华东师大版数学九年级上册 23.6.2 图形的变换与坐标教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 68.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 17:19:43 | ||
图片预览

文档简介
课题:图形的变换与坐标
【教学目标】
1.知识与技能.
理解点或图形的变化引起的坐标的变化规律,以及图形上的点的坐标的某种变化引起的图形变换,并应用于实际问题中.
2.过程与方法.
经历图形坐标变化与图形平移、旋转、放大、缩小等之间的关系,发展学生的形象思维.
3.情感、态度与价值观.
培养数形结合的思想,感受图形上点的坐标变化与图形变化之间的关系,认识其应用价值.
【重点难点】
重点:图形坐标变化与图形变换之间的关系.
难点:图形坐标变化与图形变换规律的探究.
【教学过程】
创设情境 引入课题
问题1.我们学过哪些图形的变换?
问题2.这些变换的共同特征是什么?
问题3.图形的位置发生了改变,那么图形上点的坐标会如何改变呢?
现在我们带着问题一起来探究。
首先我们一起来猜个谜语
四四方方一座城,城里兵马闹盈盈,各人指挥十六兵,不用刀枪争输赢。
大家猜一猜,谜底是什么?(中国象棋)
那么在下棋时所走的每一步是不是都可以看做平移呢?类似于棋子位置的移动,我们怎样用数学的观点,用数据来刻画图形的平移呢?
二、合作交流 探究新知
探究1:平移变换与坐标
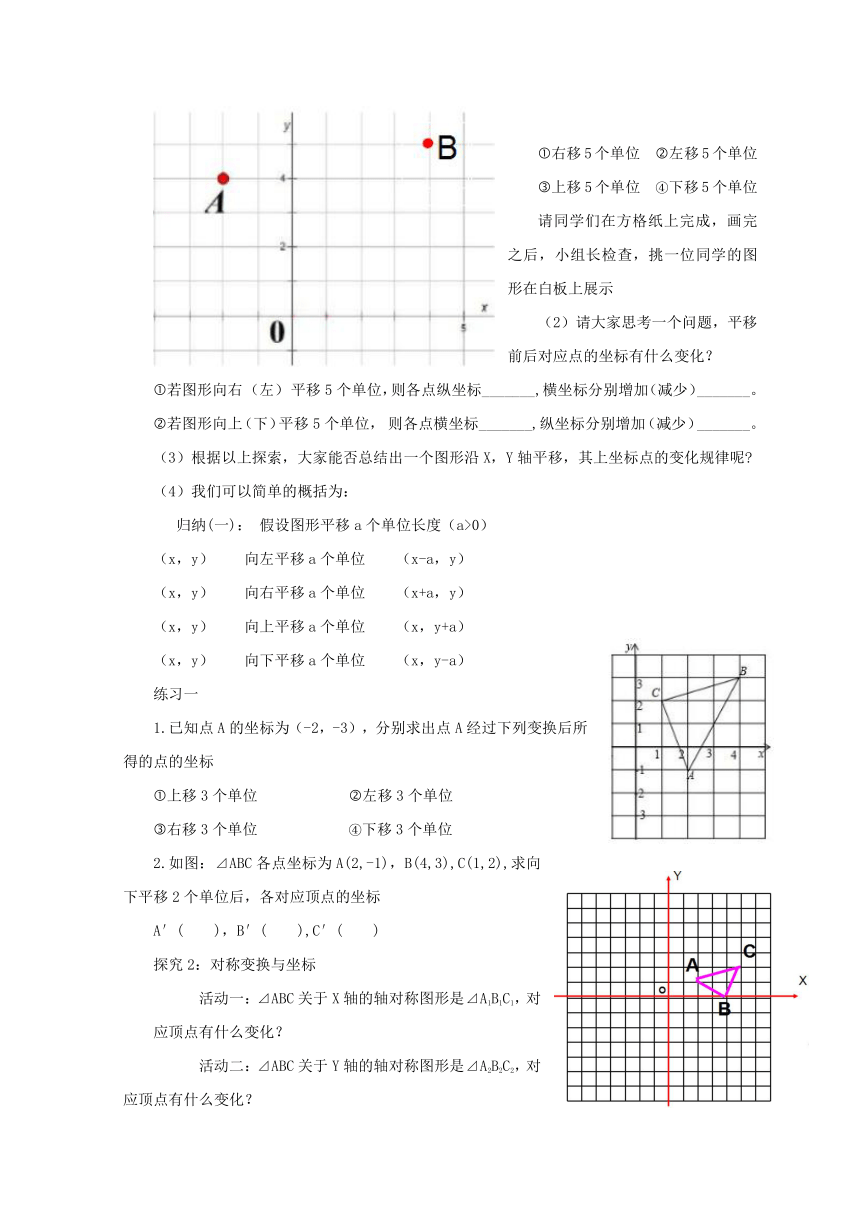
将点A(-2,4),B(4,5)分别作以下平移变换,并写出平移后点的坐标。
右移5个单位 左移5个单位
上移5个单位 ④下移5个单位
请同学们在方格纸上完成,画完之后,小组长检查,挑一位同学的图形在白板上展示
请大家思考一个问题,平移前后对应点的坐标有什么变化?
若图形向右 (左) 平移5个单位,则各点纵坐标_______,横坐标分别增加(减少)_______。
若图形向上(下)平移5个单位, 则各点横坐标_______,纵坐标分别增加(减少)_______。
(3)根据以上探索,大家能否总结出一个图形沿X,Y轴平移,其上坐标点的变化规律呢
(4)我们可以简单的概括为:
归纳(一): 假设图形平移a个单位长度(a>0)
(x,y) 向左平移a个单位 (x-a,y)
(x,y) 向右平移a个单位 (x+a,y)
(x,y) 向上平移a个单位 (x,y+a)
(x,y) 向下平移a个单位 (x,y-a)
练习一
1.已知点A的坐标为(-2,-3),分别求出点A经过下列变换后所得的点的坐标
上移3个单位 左移3个单位
右移3个单位 ④下移3个单位
2.如图:⊿ABC各点坐标为A(2,-1),B(4,3),C(1,2),求向下平移2个单位后,各对应顶点的坐标
A′( ),B′( ),C′( )
探究2:对称变换与坐标
活动一:⊿ABC关于X轴的轴对称图形是⊿A1B1C1,对应顶点有什么变化?
活动二:⊿ABC关于Y轴的轴对称图形是⊿A2B2C2,对应顶点有什么变化?
活动三:⊿ABC关于原点的对称图形是⊿A3B3C3, 对应顶点有什么变化?
根据刚才我们的画图情况,我们能否归纳出图形的对称的变换规律呢?
(x,y) 关于x轴对称 (x,-y)
(x,y) 关于y轴对称 (-x,y)
(x,y) 关于原点对称 (-x,-y)
练习二
A(1,3)关于X轴对称后点的坐标为_______,关于Y轴对称后点的坐标为_______
关于原点对称后点的坐标为_______。
平面直角坐标系中,将A(1,2)的横坐标乘以-1,纵坐标不变,得到点A′(-1,2),则点A与A′的位置关系是_______。
探究3:位似变换与坐标
如图表示⊿AOB和它以点O为位似中心缩小后得到的⊿COD。思考:
(1)它们的位似比是多少?对应顶点的坐标有什么变化?
(2)如果以点O为位似中心,位似比为二分之一,我们还有其他画法吗?其对应顶点坐标又有什么变化呢?
(3)请同学们以△COD为原图形,以点O为位似中心扩大后得到⊿AOB,参照以上思路,看能得到什么结论
(4)请同学们以小组为单位,小组合作,归纳总结最后一个规律
归纳(三)
若k>1,整个图形被扩大
若0(x,y) 原点同侧 (kx,ky)
原点异侧 (-kx,-ky)
(4)那么对于任意位置的位似三角形都有这样的变化规律吗?
举例:上图中,我们以点B为位似中心,位似比为二分之一,得到位似三角形,发现各对应顶点坐标的变化并不符合以上规律。
当堂训练 拓展提升
1.画出⊿ABC向下平移4个单位后的图形
2.画出⊿ABC关于原点对称的图形
3.以O为位似中心,将⊿ABC放大2
四、课堂小结
本节课的收获
五、布置作业
课本P78习题第1,2,3题.
【教学目标】
1.知识与技能.
理解点或图形的变化引起的坐标的变化规律,以及图形上的点的坐标的某种变化引起的图形变换,并应用于实际问题中.
2.过程与方法.
经历图形坐标变化与图形平移、旋转、放大、缩小等之间的关系,发展学生的形象思维.
3.情感、态度与价值观.
培养数形结合的思想,感受图形上点的坐标变化与图形变化之间的关系,认识其应用价值.
【重点难点】
重点:图形坐标变化与图形变换之间的关系.
难点:图形坐标变化与图形变换规律的探究.
【教学过程】
创设情境 引入课题
问题1.我们学过哪些图形的变换?
问题2.这些变换的共同特征是什么?
问题3.图形的位置发生了改变,那么图形上点的坐标会如何改变呢?
现在我们带着问题一起来探究。
首先我们一起来猜个谜语
四四方方一座城,城里兵马闹盈盈,各人指挥十六兵,不用刀枪争输赢。
大家猜一猜,谜底是什么?(中国象棋)
那么在下棋时所走的每一步是不是都可以看做平移呢?类似于棋子位置的移动,我们怎样用数学的观点,用数据来刻画图形的平移呢?
二、合作交流 探究新知
探究1:平移变换与坐标
将点A(-2,4),B(4,5)分别作以下平移变换,并写出平移后点的坐标。
右移5个单位 左移5个单位
上移5个单位 ④下移5个单位
请同学们在方格纸上完成,画完之后,小组长检查,挑一位同学的图形在白板上展示
请大家思考一个问题,平移前后对应点的坐标有什么变化?
若图形向右 (左) 平移5个单位,则各点纵坐标_______,横坐标分别增加(减少)_______。
若图形向上(下)平移5个单位, 则各点横坐标_______,纵坐标分别增加(减少)_______。
(3)根据以上探索,大家能否总结出一个图形沿X,Y轴平移,其上坐标点的变化规律呢
(4)我们可以简单的概括为:
归纳(一): 假设图形平移a个单位长度(a>0)
(x,y) 向左平移a个单位 (x-a,y)
(x,y) 向右平移a个单位 (x+a,y)
(x,y) 向上平移a个单位 (x,y+a)
(x,y) 向下平移a个单位 (x,y-a)
练习一
1.已知点A的坐标为(-2,-3),分别求出点A经过下列变换后所得的点的坐标
上移3个单位 左移3个单位
右移3个单位 ④下移3个单位
2.如图:⊿ABC各点坐标为A(2,-1),B(4,3),C(1,2),求向下平移2个单位后,各对应顶点的坐标
A′( ),B′( ),C′( )
探究2:对称变换与坐标
活动一:⊿ABC关于X轴的轴对称图形是⊿A1B1C1,对应顶点有什么变化?
活动二:⊿ABC关于Y轴的轴对称图形是⊿A2B2C2,对应顶点有什么变化?
活动三:⊿ABC关于原点的对称图形是⊿A3B3C3, 对应顶点有什么变化?
根据刚才我们的画图情况,我们能否归纳出图形的对称的变换规律呢?
(x,y) 关于x轴对称 (x,-y)
(x,y) 关于y轴对称 (-x,y)
(x,y) 关于原点对称 (-x,-y)
练习二
A(1,3)关于X轴对称后点的坐标为_______,关于Y轴对称后点的坐标为_______
关于原点对称后点的坐标为_______。
平面直角坐标系中,将A(1,2)的横坐标乘以-1,纵坐标不变,得到点A′(-1,2),则点A与A′的位置关系是_______。
探究3:位似变换与坐标
如图表示⊿AOB和它以点O为位似中心缩小后得到的⊿COD。思考:
(1)它们的位似比是多少?对应顶点的坐标有什么变化?
(2)如果以点O为位似中心,位似比为二分之一,我们还有其他画法吗?其对应顶点坐标又有什么变化呢?
(3)请同学们以△COD为原图形,以点O为位似中心扩大后得到⊿AOB,参照以上思路,看能得到什么结论
(4)请同学们以小组为单位,小组合作,归纳总结最后一个规律
归纳(三)
若k>1,整个图形被扩大
若0
原点异侧 (-kx,-ky)
(4)那么对于任意位置的位似三角形都有这样的变化规律吗?
举例:上图中,我们以点B为位似中心,位似比为二分之一,得到位似三角形,发现各对应顶点坐标的变化并不符合以上规律。
当堂训练 拓展提升
1.画出⊿ABC向下平移4个单位后的图形
2.画出⊿ABC关于原点对称的图形
3.以O为位似中心,将⊿ABC放大2
四、课堂小结
本节课的收获
五、布置作业
课本P78习题第1,2,3题.
