2021-2022学年人教版八年级数学上册12.3 角的平分线的性质同步练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.3 角的平分线的性质同步练习(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 435.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-09 11:17:37 | ||
图片预览

文档简介
12.3 角的平分线的性质—2021-2022学年八年级数学人教版
1.在中,,,的平分线AD交BC于点D,且,则点D到AB的距离等于( )
A.3 B.4 C.5 D.6
2.作的平分线时,以O为圆心,某一长度为半径作弧,与OA,OB分别相交于C,D,然后分别以C,D为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 B.等于 C.小于 D.以上都不对
3.如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
①在的平分线上;
②在的平分线上;
③在的平分线上;
④恰在,,的平分线的交点处.
上述结论中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知在中,CD是AB边上的高线,BE平分,交CD于点E,,,则的面积等于( )
A.6 B.9 C.15 D.18
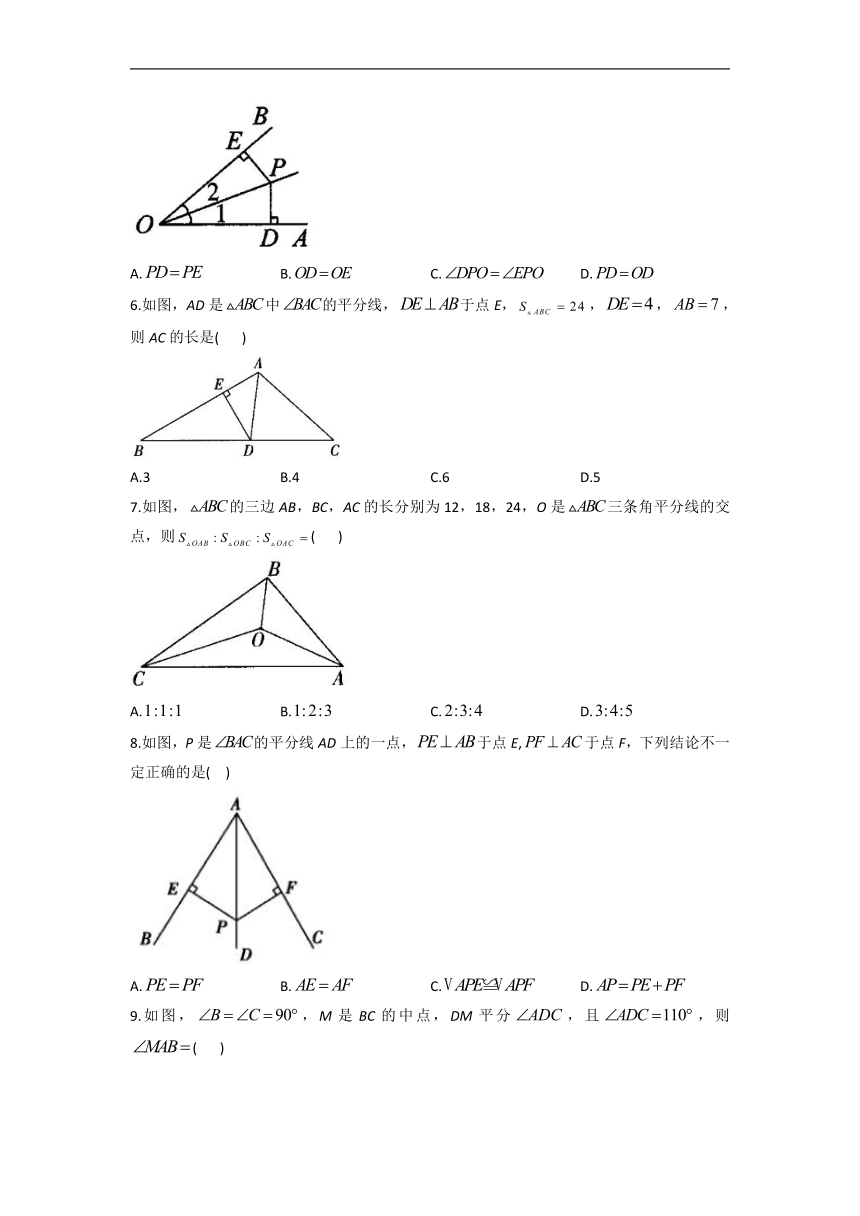
5.如图,,垂足分别为D,E,下列结论中错误的是( )
A. B. C. D.
6.如图,AD是中的平分线,于点E,,,,则AC的长是( )
A.3 B.4 C.6 D.5
7.如图,的三边AB,BC,AC的长分别为12,18,24,O是三条角平分线的交点,则( )
A. B. C. D.
8.如图,P是的平分线AD上的一点,于点E,于点F,下列结论不一定正确的是( )
A. B. C. D.
9.如图,,M是BC的中点,DM平分,且,则( )
A.30° B.35° C.45° D.60°
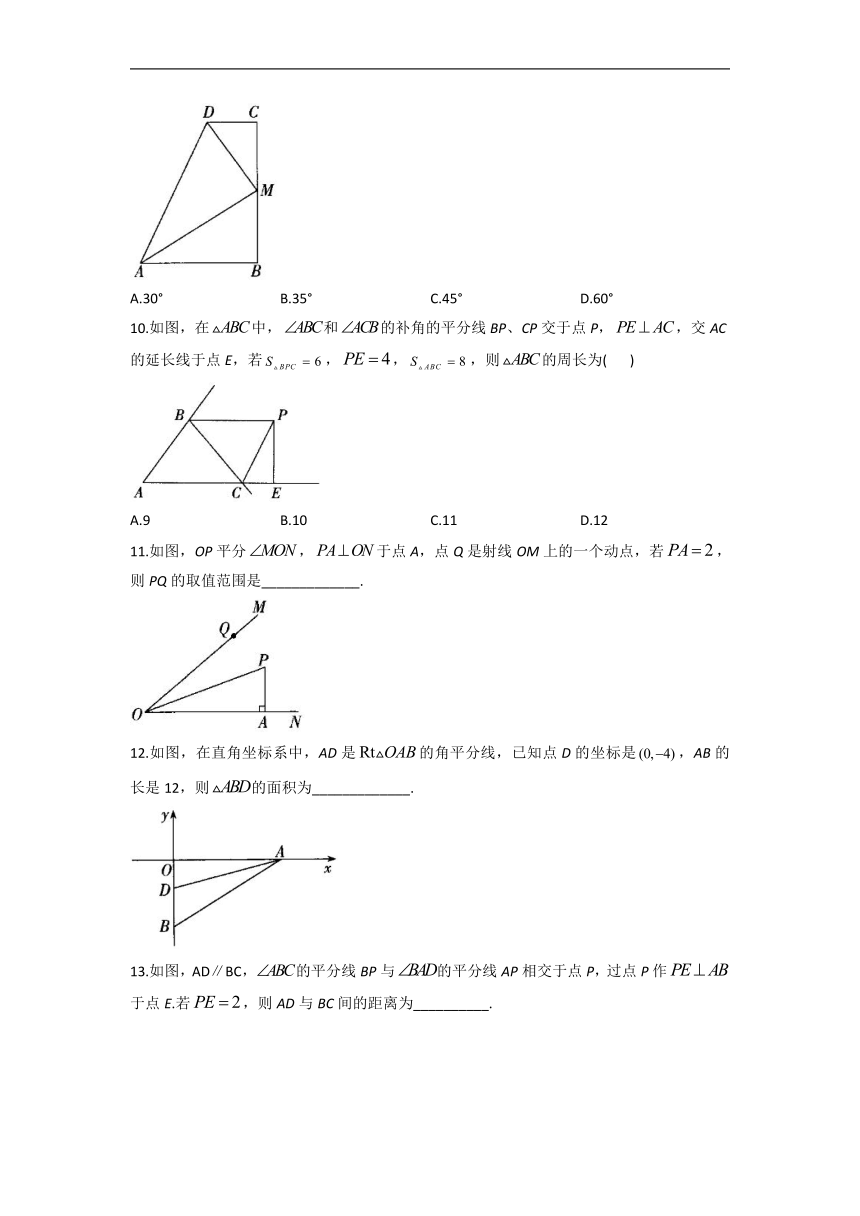
10.如图,在中,和的补角的平分线BP、CP交于点P,,交AC的延长线于点E,若,,,则的周长为( )
A.9 B.10 C.11 D.12
11.如图,OP平分,于点A,点Q是射线OM上的一个动点,若,则PQ的取值范围是_____________.
12.如图,在直角坐标系中,AD是的角平分线,已知点D的坐标是,AB的长是12,则的面积为_____________.
13.如图,AD∥BC,的平分线BP与的平分线AP相交于点P,过点P作于点E.若,则AD与BC间的距离为__________.
14.如图,AD平分,BD平分,,E为垂足,的周长为20 cm,面积为40,则DE的长为___________.
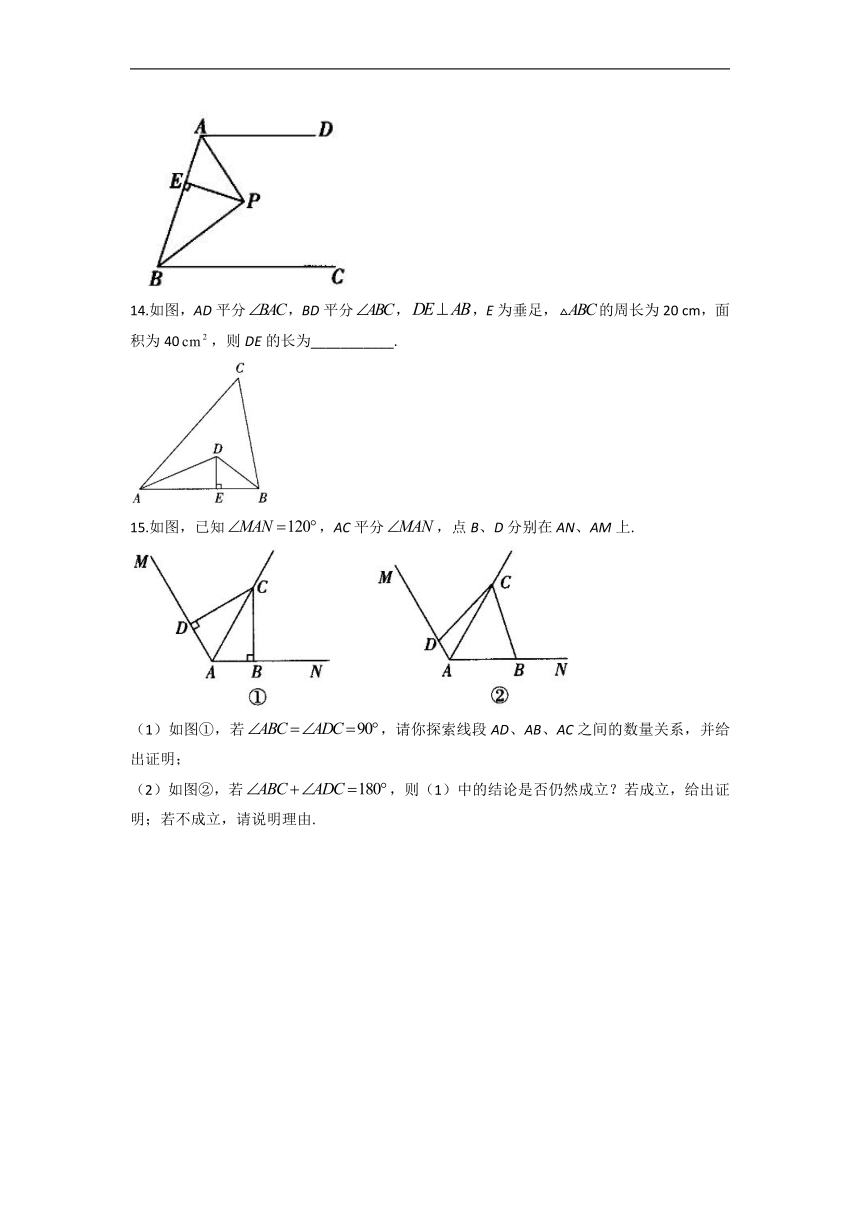
15.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
答案以及解析
1.答案:C
2.答案:A
解析:适当的长度为大于.
3.答案:D
解析:由点P到BE、BD、AC的距离恰好相等和角平分线的判定可知①②③④都是正确的.
4.答案:C
解析:如图,作于H,
BE平分,CD是AB边上的高线,,,,的面积,故选C.
5.答案:D
解析:由题中条件,可证,所以,PD和OD的等量关系无法证明,故选D.
6.答案:D
解析:如图,过点D作于F,
AD是中的平分线,,,,,,,.故选D.
7.答案:C
解析: O是三条角平分线的交点,AB,BC,AC的长分别为12,18,24,.故选C.
8.答案:D
解析:因为P是的平分线AD上的一点,,所以,所以,所以.根据题中信息,无法判断AP与的关系.故选D.
9.答案:B
解析:如图,作于N,,,,
DM平分,,,
,
M是BC的中点,
,,
又,,
,故选B.
10.答案:B
解析:如图,过点P作于F,作,交AB的延长线于G,连接AP, BP、CP分别平分,,,,,解得,,,的周长,故选B.
11.答案:
解析:PQ垂直于OM时,由角平分线的性质得,,即PQ最小,所以PQ的取值范围是.
12.答案:24
解析:如图,作于E,点D的坐标是,, AD是的角平分线,,.
13.答案:4
解析:如图,过点P作,分别交AD,BC于点M,N.因为,,所以.因为的平分线BP与的平分线AP相交于点P,,所以, ,所以.
14.答案:4 cm
解析:如图,连接CD, AD平分,BD平分,点D到AC,AB,BC的距离相等,距离都等于DE的长,的周长为20 cm,面积为40,,即,cm.
15.答案:(1).
证明: AC平分,,
,
又,
,
则.
.
(2)仍然成立.
证明:如图,过点C分别作AM、AN的垂线,垂足分别为E、F,
AC平分,
(角平分线上的点到角两边的距离相等),
,,
,
又,
,
,,
由(1)可知,
.
1.在中,,,的平分线AD交BC于点D,且,则点D到AB的距离等于( )
A.3 B.4 C.5 D.6
2.作的平分线时,以O为圆心,某一长度为半径作弧,与OA,OB分别相交于C,D,然后分别以C,D为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 B.等于 C.小于 D.以上都不对
3.如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
①在的平分线上;
②在的平分线上;
③在的平分线上;
④恰在,,的平分线的交点处.
上述结论中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知在中,CD是AB边上的高线,BE平分,交CD于点E,,,则的面积等于( )
A.6 B.9 C.15 D.18
5.如图,,垂足分别为D,E,下列结论中错误的是( )
A. B. C. D.
6.如图,AD是中的平分线,于点E,,,,则AC的长是( )
A.3 B.4 C.6 D.5
7.如图,的三边AB,BC,AC的长分别为12,18,24,O是三条角平分线的交点,则( )
A. B. C. D.
8.如图,P是的平分线AD上的一点,于点E,于点F,下列结论不一定正确的是( )
A. B. C. D.
9.如图,,M是BC的中点,DM平分,且,则( )
A.30° B.35° C.45° D.60°
10.如图,在中,和的补角的平分线BP、CP交于点P,,交AC的延长线于点E,若,,,则的周长为( )
A.9 B.10 C.11 D.12
11.如图,OP平分,于点A,点Q是射线OM上的一个动点,若,则PQ的取值范围是_____________.
12.如图,在直角坐标系中,AD是的角平分线,已知点D的坐标是,AB的长是12,则的面积为_____________.
13.如图,AD∥BC,的平分线BP与的平分线AP相交于点P,过点P作于点E.若,则AD与BC间的距离为__________.
14.如图,AD平分,BD平分,,E为垂足,的周长为20 cm,面积为40,则DE的长为___________.
15.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
答案以及解析
1.答案:C
2.答案:A
解析:适当的长度为大于.
3.答案:D
解析:由点P到BE、BD、AC的距离恰好相等和角平分线的判定可知①②③④都是正确的.
4.答案:C
解析:如图,作于H,
BE平分,CD是AB边上的高线,,,,的面积,故选C.
5.答案:D
解析:由题中条件,可证,所以,PD和OD的等量关系无法证明,故选D.
6.答案:D
解析:如图,过点D作于F,
AD是中的平分线,,,,,,,.故选D.
7.答案:C
解析: O是三条角平分线的交点,AB,BC,AC的长分别为12,18,24,.故选C.
8.答案:D
解析:因为P是的平分线AD上的一点,,所以,所以,所以.根据题中信息,无法判断AP与的关系.故选D.
9.答案:B
解析:如图,作于N,,,,
DM平分,,,
,
M是BC的中点,
,,
又,,
,故选B.
10.答案:B
解析:如图,过点P作于F,作,交AB的延长线于G,连接AP, BP、CP分别平分,,,,,解得,,,的周长,故选B.
11.答案:
解析:PQ垂直于OM时,由角平分线的性质得,,即PQ最小,所以PQ的取值范围是.
12.答案:24
解析:如图,作于E,点D的坐标是,, AD是的角平分线,,.
13.答案:4
解析:如图,过点P作,分别交AD,BC于点M,N.因为,,所以.因为的平分线BP与的平分线AP相交于点P,,所以, ,所以.
14.答案:4 cm
解析:如图,连接CD, AD平分,BD平分,点D到AC,AB,BC的距离相等,距离都等于DE的长,的周长为20 cm,面积为40,,即,cm.
15.答案:(1).
证明: AC平分,,
,
又,
,
则.
.
(2)仍然成立.
证明:如图,过点C分别作AM、AN的垂线,垂足分别为E、F,
AC平分,
(角平分线上的点到角两边的距离相等),
,,
,
又,
,
,,
由(1)可知,
.
